Факторы влияющие на теплоемкость: понятие о теплоемкости; факторы, оказывающие влияние на теплоемкость; способы задания теплоемкостей; закон Майера; теплоемкость газовой смеси. — Студопедия
Теплоёмкость — Википедия
Материал из Википедии — свободной энциклопедии
Теплоёмкость — физическая величина, определяемая как количество теплоты, которое необходимо подвести к телу в данном процессе, чтобы его температура возросла на один кельвин[1][2]:
C=δQdT.{\displaystyle C={\delta Q \over dT}.}
Во многих важных случаях приращение температуры тела прямо пропорционально сообщённому ему количеству теплоты и теплоёмкость тела является константой. В общем случае теплоёмкость тела может зависеть от параметров состояния этого тела, например его температуры или объёма[1][2].
Удельная, молярная и объёмная теплоёмкости
Очевидно, что чем больше масса тела, тем больше требуется теплоты для его нагревания, и теплоёмкость тела пропорциональна количеству вещества, содержащегося в нём. Количество вещества может характеризоваться массой или количеством молей. Поэтому удобно пользоваться понятиями удельной теплоёмкости (теплоёмкости единицы массы тела):
- c=Cm{\displaystyle c={C \over m}}
и молярной теплоёмкости (теплоёмкости одного моля вещества):
- Cμ=Cν,{\displaystyle C_{\mu }={C \over \nu },}
где ν=mμ{\displaystyle \nu ={m \over \mu }} — количество вещества в теле; m{\displaystyle m} — масса тела; μ{\displaystyle \mu } — молярная масса. Молярная и удельная теплоёмкости связаны соотношением Cμ=cμ{\displaystyle C_{\mu }=c\mu }[1][2].
Объёмная теплоёмкость (теплоёмкость единицы объёма тела):
- C′=CV.{\displaystyle C’={C \over V}.}
Теплоёмкость для различных процессов и состояний вещества
Понятие теплоёмкости определено как для веществ в различных агрегатных состояниях (твёрдых тел, жидкостей, газов), так и для ансамблей частиц и квазичастиц (в физике металлов, например, говорят о теплоёмкости электронного газа).
Теплоёмкость идеального газа
Теплоёмкость системы невзаимодействующих частиц (например, идеального газа) определяется числом степеней свободы частиц.
Молярная теплоёмкость при постоянном объёме:
- CV=dUdT=i2R,{\displaystyle C_{V}={dU \over dT}={\frac {i}{2}}R,}
где R{\displaystyle R} ≈ 8,31 Дж/(моль·К) — универсальная газовая постоянная, i{\displaystyle i} — число степеней свободы молекулы[1][2].
Молярная теплоёмкость при постоянном давлении[1][2]:
- CP=dUdT+PdVdT=i+22R.{\displaystyle C_{P}={dU \over dT}+{PdV \over dT}={{i+2} \over 2}R.}
Теплоёмкость кристаллов
Теория теплоёмкости
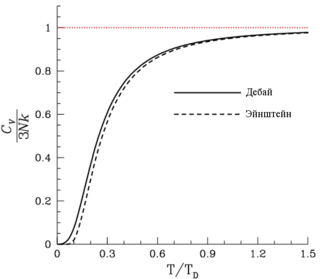 Сравнение моделей Дебая и Эйнштейна для теплоёмкости твёрдого тела
Сравнение моделей Дебая и Эйнштейна для теплоёмкости твёрдого тела
Существует несколько теорий теплоёмкости твердого тела:
Существующие теории теплоёмкости не охватывают всех особенностей поведения теплоёмкости различных твёрдых тел. В первую очередь это относится к аномальным пикам на кривых теплоёмкости, а также росту в высокотемпературной области удельной теплоёмкости над уровнем 3R нормальной (колебательной) составляющей. Возникновение некоторых из перечисленных аномалий детально исследовано и имеет своё физическое объяснение. Это в первую очередь относится к лямбда-пикам, связанным с ферромагнитными и ориентационными переходами, а также с переходами от упорядоченных к неупорядоченным структурам. Аномальные отклонения над уровнем 3R кривой теплоёмкости графита и алмаза в высокотемпературной области (Т > 3000 K) обусловлены процессами термодеструкции с переходом в плавление. Аномальные пики на кривых теплоёмкости германия и гафния объясняются процессами в кристаллической решетке, контролируемыми больцмановским фактором exp(-E/RT).
Примечания
- ↑ 1 2 3 4 5 Никеров. В. А. Физика: учебник и практикум для академического бакалавриата. — Юрайт, 2015. — С. 127—129. — 415 с. — ISBN 978-5-9916-4820-2.
- ↑ 1 2 3 4 5 Ильин В. А. Физика: учебник и практикум для прикладного бакалавриата. — Юрайт, 2016. — С. 142—143. — 399 с. — ISBN 978-5-9916-6343-4.
Литература
Теплоемкость – это… Чему равна теплоемкость? Таблица теплоемкости
Теплоемкость – это способность поглощать некоторые объемы тепла во время нагревания или отдавать при охлаждении. Теплоемкость тела – это отношение бесконечно малого числа теплоты, что получает тело, к соответствующему приросту его температурных показателей. Величина измеряется в Дж/К. На практике применяют немного другую величину – удельную теплоемкость.
Определение

Что означает удельная теплоемкость? Это величина, относящаяся к единичному количеству вещества. Соответственно, численность вещества можно измерить в кубометрах, килограммах или даже в молях. От чего это зависит? В физике теплоемкость зависит напрямую от того, к какой количественной единице она относиться, а значит, различают молярную, массовую и объемную теплоемкость. В строительной сфере вы не будете встречаться с молярными измерениями, но с другими – сплошь и рядом.
Что влияет на удельную теплоемкость?

Что такое теплоемкость, вы знаете, но вот какие значения влияют на показатель, еще не ясно. На значение удельной теплоемкости напрямую воздействуют несколько компонентов: температура вещества, давление и иные термодинамические характеристики.
Во время роста температуры продукции его удельная теплоемкость растет, однако определенные вещества отличаются совершенно нелинейной кривой в этой зависимости. Например, с возрастанием температурных показателей с нуля до тридцати семи градусов удельная теплоемкость воды начинает понижаться, а если предел будет находиться между тридцатью семью и ста градусами, то показатель, наоборот, возрастет.
Стоит отметить, что параметр зависит еще и от того, каким образом разрешается изменяться термодинамическим характеристикам продукции (давлению, объему и так далее). Например, удельная теплоемкость при стабильном давлении и при стабильном объеме будут отличаться.
Как рассчитать параметр?
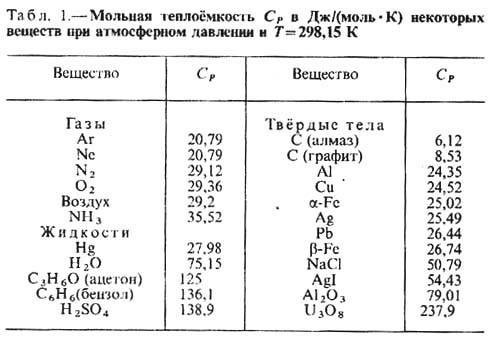
Вас интересует, чему равна теплоемкость? Формула расчета следующая: С=Q/(m·ΔT). Что это за значения такие? Q – это количество теплоты, что получает продукция при нагреве (или же выделяемое продукцией во время охлаждения). m — масса продукции, а ΔT — разность окончательной и начальной температур продукции. Ниже приведена таблица теплоемкости некоторых материалов.
Что можно сказать о вычислении теплоемкости?
Вычислить теплоемкость – это задача не из самых простых, особенно если применять исключительно термодинамические методы, точнее это невозможно сделать. Потому физики используют методы статистической физики или же знания микроструктуры продукции. Как произвести вычисления для газа? Теплоемкость газа рассчитывается из вычисления средней энергии теплового движения отдельно взятых молекул в веществе. Движения молекул могут быть поступательного и вращательного типа, а внутри молекулы может быть целый атом или колебание атомов. Классическая статистика говорит, что на каждую степень свободы вращательных и поступательных движений приходится в мольной теплоемкости газа величина, что равняется R/2, а на каждую колебательную степень свободы значение равняется R. Это правило еще именуют законом равнораспределения.
При этом частичка одноатомного газа отличается всего тремя поступательными степенями свободы, а потому его теплоемкость должна приравниваться к 3R/2, что отлично согласуется с опытом. Каждая молекула двухатомного газа отличается тремя поступательными, двумя вращательными и одной колебательной степенями свободы, а значит, закон равнораспределения будет равняться 7R/2, а опыт показал, что теплоемкость моля двухатомного газа при обычной температуре составляет 5R/2. Почему оказалось такое расхождение теории? Все связано с тем, что при установлении теплоемкости потребуется учитывать разные квантовые эффекты, другими словами, пользоваться квантовой статистикой. Как видите, теплоемкость – это довольно-таки сложное понятие.
Квантовая механика говорит, что любая система частичек, что совершают колебания или же вращения, в том числе и молекула газа, может иметь определенные дискретные значения энергии. Если же энергия теплового движения в установленной системе недостаточна для возбуждения колебаний необходимой частоты, то данные колебания не вносят вклада в теплоемкость системы.
В твердых телах тепловое движение атомов являет собой слабые колебания поблизости определенных положений равновесия, это касается узлов кристаллической решетки. Атом обладает тремя колебательными степенями свободы и по закону мольная теплоемкость твердого тела приравнивается к 3nR, где n– количество имеющихся атомов в молекуле. На практике это значение является пределом, к которому стремится теплоемкость тела при высоких температурных показателях. Значение достигается при обычных температурных изменениях у многих элементов, это касается металлов, а также простых соединений. Также определяется теплоемкость свинца и других веществ.
Что можно сказать о низких температурах?

Мы уже знаем, что такое теплоемкость, но если говорить о низких температурах, то как значение будет рассчитываться тогда? Если речь идет о низких температурных показателях, то теплоемкость твердого тела тогда оказывается пропорциональной T 3 или же так называемый закон теплоемкости Дебая. Главный критерий, позволяющий отличить высокие показатели температуры от низких, является обычное сравнение их с характерным для определенного вещества параметром – это может быть характеристическая или температура Дебая qD. Представленная величина устанавливается спектром колебания атомов в продукции и существенно зависит от кристаллической структуры.
У металлов определенный вклад в теплоемкость дают электроны проводимости. Данная часть теплоемкости высчитывается с помощью статистики Ферми-Дирака, в которой учитываются электроны. Электронная теплоемкость металла пропорциональная обычной теплоемкости, представляет собой сравнительно небольшую величину, а вклад в теплоемкость металла она вносит только при температурных показателях, близких к абсолютному нулю. Тогда решеточная теплоемкость становится очень маленькой, и ею можно пренебречь.
Массовая теплоемкость
Массовая удельная теплоемкость – это количество теплоты, что требуется поднести к единице массы вещества, дабы нагреть продукт на единицу температуры. Обозначается данная величина буквой С и измеряется она в джоулях, поделенных на килограмм на кельвин – Дж/(кг·К). Это все, что касается теплоемкости массовой.
Что такое объемная теплоемкость?
Объемная теплоемкость – это определенное количество теплоты, что требуется подвести к единице объема продукции, дабы нагреть ее на единицу температуры. Измеряется данный показатель в джоулях, поделенных на кубический метр на кельвин или Дж/(м³·К). Во многих строительных справочниках рассматривают именно массовую удельную теплоемкость в работе.
Применение на практике теплоемкости в строительной сфере
Многие теплоемкие материалы применяют активно при строительстве теплоустойчивых стен. Это крайне важно для домов, отличающихся периодическим отоплением. Например, печным. Теплоемкие изделия и стены, возведенные из них, отлично аккумулируют тепло, запасают его в отопительные периоды времени и поэтапно отдают тепло после выключения системы, позволяя таким образом поддерживать приемлемую температуру на протяжении суток.
Итак, чем больше будет запасено тепла в конструкции, тем комфортней и стабильней будет температура в комнатах.
Стоит отметить, что обычный кирпич и бетон, применяемые в домостроении, обладают значительно меньшей теплоемкостью, чем пенополистирол. Если брать эковату, то она в три раза более теплоемкая, нежели бетон. Следует отметить, что в формуле расчета теплоемкости совершенно не зря присутствует масса. Благодаря большой огромная массе бетона или кирпича в сравнении с эковатой позволяет в каменных стенах конструкций аккумулировать огромные объемы тепла и сглаживать все суточные температурные колебания. Только малая масса утеплителя во всех каркасных домах, несмотря на хорошую теплоемкость, является самой слабой зоной у всех каркасных технологий. Чтобы решить данную проблему, во всех домах монтируют внушительные теплоаккумуляторы. Что это такое? Это конструктивные детали, отличающиеся большой массой при достаточно хорошем показателе теплоемкости.
Примеры теплоаккумуляторов в жизни

Что это может быть? К примеру, какие-то внутренние кирпичные стены, большая печь или камин, стяжки из бетона.
Мебель в любом доме или квартире является отличным теплоаккумулятором, ведь фанера, ДСП и дерево фактически в три раза больше могут запасаться теплом лишь на килограмм веса, нежели пресловутый кирпич.
Есть ли недостатки в теплоаккумуляторах? Конечно, главный минус данного подхода состоит в том, что теплоаккумулятор требуется проектировать еще на стадии создания макета каркасного дома. Все из-за того, что он отличается большим весом, и это потребуется учесть при создании фундамента, а после еще представить, как данный объект будет интегрирован в интерьер. Стоит сказать, что учитывать придется не только массу, потребуется оценивать в работе обе характеристики: массу и теплоемкость. К примеру, если применять золото с невероятным весом в двадцать тонн на кубометр в качестве теплоаккумулятора, то продукция будет функционировать как нужно лишь на двадцать три процента лучше, нежели бетонный куб, вес которого составляет две с половиной тонны.
Какое вещество больше всего подходит для теплоаккумулятора?

Наилучшим продуктом для теплоаккумулятора является совсем не бетон и кирпич! Неплохо с этой задачей справляется медь, бронза и железо, но они очень тяжелые. Как ни странно, но лучший теплоаккумулятор – вода! Жидкость имеет внушительную теплоемкость, самую большую среди доступных нам веществ. Больше теплоемкость только у газов гелия (5190 Дж/(кг·К) и водорода (14300 Дж/(кг·К), но их проблематично применять на практике. При желании и необходимости смотрите таблицу теплоемкости нужных вам веществ.
Факторы, влияющие па величину — Справочник химика 21
Какие факторы влияют на величину электродного потенциала [c.35]
Какие факторы влияют на величину электродного потенциала Напишите уравнение, выражающее зависимость электродного потенциала от факторов, влияющих на его величину. [c.74]
Что такое теплоемкость и какие факторы влияют на ее величину [c.109]
Необходимо рассматривать зазоры между цилиндром и поршнем в плоскости качания шатуна и в плоскости оси поршневого пальца, так как при выборе зазора одни и те же факторы влияют различно в этих плоскостях. Так, например, температурные и силовые деформации поршня в этих плоскостях по-разному влияют на величину зазора в сопряжении поршень— цилиндр. В плоскости качания шатуна они увеличивают величину зазора, а в плоскости оси вращения коленчатого вала и оси поршневого пальца уменьшают ее. За счет зазора в сопряжении поршень—цилиндр в плоскости качания шатуна обеспечивается жидкостное трение поршня о зеркало цилиндра. [c.71]
На вопрос, каков следующий этап расчета реактора, некоторые студенты, не подумав, отвечают, что далее определяется время пребывания, необходимое для протекания реакции до требуемой степени превращения. Но это по существу уже было сделано. Величина ПО выражает объем реактора, обеспечивающего требуемое время пребывания при заданной скорости потока Следующая стадия расчета, которая теперь выходит за рамки химической кинетики, заключается в выборе отношения диаметра к длине. Какие же инженерные факторы влияют на этот выбор [c.76]
Какие факторы влияют на величину теплового эффекта Сформулируйте закон Кирхгофа. [c.109]
На индукционный период влияет не только химический состав тошшва, но и внешние факторы — тешература, величина поверхности, соприкасающейся с воздухом, каталитическое действие металлов и т.д. [c.44]
Практически вопрос сводится к следующему какие факторы влияют на величину зета-потенциала, и каким образом можно регулировать эту величину [c.75]
На сохранность защитных пленок на металлах влияет целый ряд факторов 1) величина и характер внутренних напряжений и внешних механических нагрузок 2) механические свойства защитной нленки, в первую очередь ее прочность и пластичность [c.77]
Дисперсионный анализ состоит в выделении и оценке отдельных факторов, вызывающих изменчивость изучаемой случайной величины. Для этого производится разложение суммарной выборочной дисперсии на составляющие, обусловленные независимыми факторами. Каждая из этих составляющих представляет собой оценку дисперсии генеральной совокупности. Чтобы решить, значимо ли влияние данного фактора, необходимо оценить значимость соответствующей выборочной дисперсии в сравнении с дисперсией воспроизводимости, обусловленной случайными факторами. Проверка значимости оценок дисперсий проводится по критерию Фишера (см. гл. II, 11). Если рассчитанное значение критерия Фишера окажется меньше табличного, то влияние рассматриваемого фактора нет оснований считать значимым. Если же рассчитанное значение критерия Фишера окажется больше табличного, то рассматриваемый фактор влияет на изменчивость средних. В дальнейшем будем полагать, что выполняются следующие допущения 1) случайные ошибки наблюдений имеют нормальное распределение 2) факторы влияют только на изменение средних значений, а дисперсия наблюдений остается постоянной эксперименты равноточны. [c.75]
Кроме перечисленных выше факторов, на величину удельного электросопротивления кокса влияет содержание в нем серы и зольность его. С повышением на 1 % зольности кокса, прокаленного в пределах температур 1000—1300°С в течение [c.211]
Таким образом, кроме кинетики, еще два фактора влияют на характеристики реактора при заданной величине распределения времени пребывания взаимное расположение областей идеального смешения и идеального вытеснения и внутреннее микро- или макро-состояние жидкости. [c.310]
Каков механизм потерь металла прн электролизе расплава Какие факторы влияют на величину потерь [c.296]
Как возникает поверхностное натяжение у жидкостей и какие факторы влияют на его величину [c.70]
Что называется энтальпией растворения Какие факторы влияют на эту величину [c.64]
Многие другие кинетические факторы влияют на величину перенапряжения — скорости переноса частиц к электродам и отвода продуктов электролиза, скорость процесса разрушения гидратных и других оболочек разряжающихся ионов, скорость соединения атомов в двухатомные газовые молекулы и т. п. [c.361]
Какие факторы влияют на величину стандартного и формального потенциалов [c.205]
Другим важным фактором является величина К у), которая не влияет на величину pH в ходе процесса нейтрализации, но оказывает сильное влияние в точке эквивалентности. Например, при титровании слабой кислоты сильным основанием в точке эквивалентности [c.40]
Какие факторы влияют на величину «реального стандартного потенциала» полуреакции [c.35]
На каталитическую активность твердого катализатора влияет величина и состояние поверхности катализатора, структура, наличие примесей и другие факторы. С целью увеличения поверхности соприкосновения катализатора с реагирующими веществами его применяют в тонко раздробленном виде. Обычно такой раздробленный катализатор наносят на какое-либо пористое вещество— носит
Теплоемкость — элемент — Большая Энциклопедия Нефти и Газа, статья, страница 2
Теплоемкость — элемент
Cтраница 2
Теплоемкость элементов зернистого слоя значительно выше теплоемкости газа, текущего через слой.
[16]
В последующих разделах мы приводим сводку опубликованных данных по теплоемкости твердых тел при гелиевой температуре. В части А содержатся данные по теплоемкости элементов ( кроме ожрокенных газов), размещенных в соответствии с периодической таблицей Менделеева. В части Б обсуждаются другие факторы, влияющие на теплоемкость твердых тел, и приводятся данные по теплоемкости различных соединений.
[17]
В последующих разделах мы приводим сводку опубликованных данных по теплоемкости твердых тел при гелиевой температуре. В части А содержатся данные по теплоемкости элементов ( кроме ожижешшх газов), размещенных в соответствии с периодической таблицей Менделеева.
[18]
Для твердых химических соединений существует закон, найденный Нейманом и позже тщательно проверенный Коппом: граммолекуляр-ная теплоемкость химического соединения, взятого в твердом состоянии, равна сумме гр амматомных теплоемкостей элементов, его составляющих. Однако для приложимости закона Нейманга — Коппа во многих случаях приходится считать грамматомную теплоемкость элемента отличной от шести калорий.
[19]
В основу первых методов сравнительного расчета термодинамических свойств был положен принцип аддитивности. Так, согласно правилу Коппа — Неймана теплоемкость ( Ср) химического соединения в кристаллическом состоянии равна сумме теплоемкостей элементов, или определенных инкрементов, постоянных для каждого данного элемента.
[20]
Существует и другой простой метод определения температурной зависимости теплоемкости соединения, если известно ее значение при какой-либо температуре. В этом случае исходят из предположения, что зависящая от температуры часть теплоемкости аддитивно складывается из зависящих от температуры частей теплоемкостей элементов, составляющих данное соединение. Важно только, чтобы уравнения теплоемкости относились к одинаковым агрегатным состояниям.
[21]
Применив его, Деларош и Берар ( 1814 г.) [16] впервые получили надежные значения теплоемкости газов ( при постоянном давлении), а Пти и Дюлонг ( 1819 г.) [17] измерили теплоемкости элементов и открыли закон равенства грамм-атомных теплоемкостей элементов, носящий теперь их имена.
[22]
Это необходимо для исследования плохоформализуемых конструкций с точки зрения построения объектов. Данная ветвь в подсистеме позволяет строить МТП разной степени детализации, а также исследовать новые типы конструкций РЭС с целью дальнейшего перехода к разработке модулей автоматического формирования моделей таких конструкций. В подсистеме Пилот предусмотрена возможность описывать мощности тепловыделений, теплоемкости элементов конструкции и ЭРИ, воздействующие температуры в виде различных функциональных зависимостей.
[23]
Исходными для всех дальнейших расчетов значениями энтальпии являются стандартные теплоты образования, которые по определению характеризуют образование соединений из простых веществ в стандартных состояниях. Если мы желаем подсчитать теплоты образования при температурах более высоких, чем 298 К, необходимо знать ACpf — изменение молярной теплоемкости при образовании соединения из элементов при различных температурах. Для многих соединений значения HfT табулированы в достаточно широком интервале температур. Однако при использовании приведенных в этой книге таблиц, в которых содержатся групповые вклады для вычисления ДЯ / только при 298 К, нет необходимости всегда вычислять ДЯ ( т — Это связано с тем, что, так как данная величина в большинстве случаев будет использоваться для определения теплоты реакции при температуре Т, теплоемкости элементов Срт, с помощью которых вычисляется теплота реакции, взаимно уничтожатся.
[24]
В настоящее время существуют точные методы измерения теплоемкости в широком интервале температур. Имеются определенные успехи в разработке теории теплоемкости для простого твердого вещества и для газообразного его состояния при невысоких давлениях. Что же касается удовлетворительной теории теплоемкости сложного твердого или жидкого вещества, то ее пока до сих пор не существует. Если отсутствуют экспериментальные данные для теплоемкости в твердом или в жидком состояниях, приходится прибегать для ее оценки к ряду приближенных эмпирических правил. Это правило более или менее оправдывается для элементов, атомная масса которых выше, чем у калия, и при относительно высоких температурах, близких к температурам плавления твердого вещества. Если допустить неизменяемость теплоемкостей элементов при образовании химического соединения, то теплоемкость последнего будет равна 25 / г Дж / ( моль К), где п — число атомов, входящих в молекулу. Это эмпирическое правило, которое также является приближенным, было впервые предложено Нейманом ( 1831) и в дальнейшем развито Коппом.
[25]
В настоящее время существуют точные методы измерения теплоемкости в широком интервале температур. Имеются определенные успехи в разработке теории теплоемкости для простого твердого вещества и для газообразного его состояния при невысоких давлениях. Что же касается удовлетворительной теории теплоем-кости сложного твердого или жидкого вещества, то ее пока до сих пор не существует. Если отсутствуют экспериментальные данные для теплоемкости в твердом или в жидком состояниях, приходится прибегать для ее оценки к ряду приближенных эмпирических правил. Это правило более или менее оправдывается для элементов, атомная масса которых выше, чем у калия, и при относительно высоких температурах, близких к температурам плавления твердого вещества. Если допустить неизменяемость теплоемкостей элементов при образовании химического соединения, то теплоемкость последнего будет равна 25л Дж / ( моль К), где п — число атомов, входящих в молекулу. Это эмпирическое правило, которое также является приближенным, было впервые предложено Нейманом ( 1831) и в дальнейшем развито Коппом.
[26]
Для решения всех этих вопросов нужно было определить состав различных тел, о которых существовало превратнее понятие, и тогда, имея целый ряд химических оснований для суждения о составе и строении тел, можно было приступить к подробному изучению физических свойств и сличению физических свойств с химическими и вообще к изучению химических процессов. Нужно сказать, что первые соотношения физических свойств и ( химических были указаны Гей-Люйсакам; его знаменитый закон объемов прямо указывает на отношение химических процессов к удельному весу и к объему, который занимают тела в газообразном состоянии. Затем на этом был основан закон Авогадро, что равные объемы газов заключают равное число частиц. Стали — изучать подробно удельный вес в газообразном состоянии, затем стали изучать удельный вес в твердом и жидком состоянии. Он первый указал связь между этими объемами и кристаллическими формами, то есть объяснил физическую или кристаллическую изоморфность, открытую Митчерлихом. Вскоре после откр
ФАКТОРЫ, ВЛИЯЮЩИЕ НА ТЕПЛОФИЗИЧЕСКИЕ — Студопедия
ХАРАКТЕРИСТИКИ ПОЧВЫ
Характер теплофизических характеристик почвы формируется под воздействием четырех факторов: кондуктивной, конвективной, радиационной и массообменной проводимости.
Кондукция (теплопередача) – физический процесс передачи тепловой энергии от более горячего тела к более холодному либо непосредственно (при контакте), либо через разделяющую (тела или среды) перегородку из какого-либо материала.
Кондуктивная теплопроводность в такой типичной дисперсной среде, как почва, зависит от структурной модели, под которой имеется в виду система взаимного расположения твердых частиц и пор, от химико-минералогического состава твердой фазы почвы, от соотношения между объемом промежуточной среды (газ, влага) и общим объемом системы, т. е. от ее пористости, влажности и температуры почвы.
Конвекция – явление переноса теплоты жидкостями или газами, путем их перемешивания (как вынужденно, так и самопроизвольно). В почвах рассматривается естественная конвекция, которая возникает самопроизвольно при неравномерном нагревании веществ в поле тяготения.
При, обычно распространенных размерах почвенных пор и частиц в 0,1-0,2 мм, процент общей теплопередачи за счет конвекции лежит в пределах 0,15-0,3% и только для весьма крупных частиц и пор, порядка 3,0 мм этот процент доходит до 5-5,5% при максимально возможном перепаде температур. В почвах проявление этого механизма заметно лишь при высокой влажности и быстром перемешивании свободной воды.
Радиационная проводимость – превращение внутренней энергии вещества в энергию излучения (энергию фотонов, или электромагнитных волн), перенос этого излучения в пространстве и его поглощение другим веществом.
В реальных условиях, когда почва не нагревается выше 600С, роль радиационного теплообмена пренебрежимо мала.
Массообмен предполагает перемещение влаги в почве, как в форме пара, так и в капельно-жидком виде. Этот поток влаги переносит с собой тепло, которое изменяет режим теплопереноса и влияет на величину теплофизических характеристик почвы.
Характер изменения теплофизических свойств генетических горизонтов в почвенном профиле и динамика этих свойств во времени и пространстве в значительной степени определяются влажностью, плотностью или пористостью (порозность) и механическим составом.
Теплоемкостьпочвы складывается из теплоемкостей составляющих ее почвенных фаз: твердой (Cρs), воды (Cρw) и воздуха (Cρa). Тепло будет равномерно распределяться в трехфазной почвенной системе по всем ее фазам, нагревая их в соответствии с теплоемкостью каждой из фаз и ее долей в почве. Теплоемкость почвы (Cρ), в целом составит:
Cρ = fs Cρs + fw Cρw + fa Cρa. (1)
где: fs, fw, fa — объемные доли твердой фазы, воды и воздуха.
Объемная теплоемкость абсолютно сухой почвы от пахотного горизонта к нижележащим, увеличивается, что вызвано главным образом значительным повышением объемного веса (плотность) почвы вниз по профилю.
Теплофизические параметры зависят от влажности почвы. Можно выделить три характерные области, соответствующие различным энергетическим состояниям почвенной влаги (рисунок – 1).

Рисунок – 1. Схема теплопереноса при различной степени
влажности.
1. В области низких влажностей вода прочно связана, и процессы теплообмена определяются исключительно кондуктивным механизмом переноса тепла в почве. С увеличением влажности растет площадь стыковых манжет и, соответственно, величина кондуктивной теплопроводности. Одновременно увеличивается и объемная теплоемкость, линейно зависящая от влажности. Рост теплопроводности компенсируется ростом теплоемкости, а температуропроводность в это время практически не зависит от влажности.
2. Пародиффузионный перенос достигает своего максимума: теплопроводность возрастает быстрее, чем объемная теплоемкость. Температуропроводность увеличивается с влажностью.
3. При дальнейшем повышении влажности появляется капиллярная влага, заполняющая почвенные капилляры. Теплообмен сводится к кондуктивной теплопередаче и к слабо выраженной в почве конвекции. В результате рост теплопроводности замедляется. Поскольку объемная теплоемкость продолжает увеличиваться с влажностью, температуропроводность начинает снижаться. Она достигает максимума в области влажностей, близких к влажности разрыва капилляров (ВРК) (рисунок – 2).
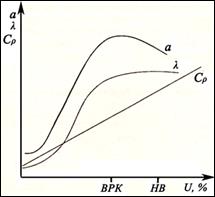
Рисунок – 2. Зависимости теплофизических параметров от влажности.
1.3.2. Уравнения состояния реальных газов
При уменьшении
удельного объема газа υ,
т.е. при увеличении р
и уменьшении Т
свойства реальных газов начинают
отличаться от свойств идеального газа.
Это связано с уменьшением расстояния
между молекулами, из-за чего увеличивается
взаимодействие между ними и сказывается
объем молекул. Поэтому использование
в расчетах модели идеального газа в
этом случае приводит к погрешностям.
Для учета свойств
реального газа был предложен ряд
уравнений реального газа. Одно из первых
уравнений предложил Ван-дер-Ваальс в
следующем виде
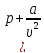 )(
)(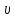 —b)=RT,
—b)=RT,
где а
и b
– постоянные коэффициенты, разные для
каждого газа. Поправка
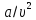 учитывает силы межмолекулярного
учитывает силы межмолекулярного
взаимодействия (внутреннее давление).
Как видно, эта поправка возрастает при
уменьшении удельного объема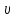 .
.
Поправкаb
учитывает объем, занимаемый молекулами.
Уравнение
Ван-дер-Ваальса качественно хорошо
описывает изменение свойств реальных
газов при изменении р
и Т,
но является приближенным.
Для количественных
расчетов используют уравнение состояния
в виде
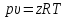 ,
,
где
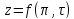 — коэффициент сжимаемости, зависящий
— коэффициент сжимаемости, зависящий
отр
и Т
и определяемый по опытным данным. Здесь
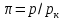 – приведенное давление,
– приведенное давление,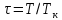 – приведенная температура, а
– приведенная температура, а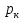 и
и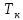 – критические значения давления и
– критические значения давления и
температуры данного вещества (см. ниже).
1.4. Термодинамический процесс. Равновесные, неравновесные
и
квазиравновесные термодинамические
процессы
Термодинамическим
процессом
называется изменение состояния системы
(тела), сопровождающееся изменением
ее параметров (р,
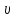 ,
,
Т).
Все
процессы могут быть разделены на
равновесные и неравновесные.
Равновесным
называется
процесс, при осуществлении которого
система
проходит
через непрерывный ряд равновесных
состояний. Следовательно, при протекании
равновесного процесса в каждый данный
момент давление и температура во всех
частях системы одинаковы.
Неравновесным
называется процесс, при протекании
которого система не находится в состоянии
равновесия. При осуществлении такого
процесса давление и температура в
различных областях системы могут быть
неодинаковы.
Реальные
процессы, протекающие в технических
устройствах, в принципе являются
неравновесными. Это объясняется тем,
что изменение состояния системы,
представляющее собой термодинамический
процесс, может быть осуществлено только
посредством внешнего воздействия путем
нарушения равновесия. Однако можно
представить такие условия протекания
реальных процессов, когда они становятся
практически равновесными
(квазиравновесными,
т.е. как
бы равновесными).
Очевидно, что для этого нарушения
равновесия в системе должны быть
бесконечно малыми; последнее может
быть достигнуто медленным изменением
состояния систем, т. е. медленным
протеканием процесса.
Рассмотрим
для примера сжатие газа в цилиндре с
помощью поршня. При движении поршня в
первую очередь будут сжиматься слои
газа, которые непосредственно прилегают
к поверхности поршня. Следовательно,
давление в этих слоях газа будут выше
среднего давления газа в цилиндре.
Поэтому в процессе сжатия давление газа
в цилиндре является неодинаковым и сам
процесс неравновесным. Передача
этого, вызванного перемещением поршня,
изменения давления происходит с конечной
скоростью, равной скорости звука. Если
скорость перемещения поршня wnмала по
сравнению со скоростью звука
а, то давление
в каждый данный момент будет успевать
выравниваться по всему объему цилиндра
и процесс будет квазиравновесным.
Наоборот, при соизмеримых значениях
wn
и
а процесс
будет неравновесным. Таким образом,
равновесный процесс является предельным
случаем неравновесного при стремлении
скорости последнего к нулю. Замена
реального процесса равновесным позволяет
для его исследования использовать
термодинамические уравнения и методы
анализа, что дает весьма плодотворные
результаты и часто очень точные.
1.5. Теплоемкость
и факторы на неё влияющие
1.5.1. Виды
теплоемкости
Теплоемкость
– это количество теплоты, поглощаемой
телом (газом), при повышении его температуры
на один градус Цельсия.
Удельная
теплоемкость
– это теплоемкость 1 кг вещества. Она
обозначается символом «с»
и имеет размерность Дж/(кг∙К).
Мольная
теплоемкость
– это теплоемкость 1 моля вещества
(сμ,
Дж/(моль∙К).
Истинная
теплоемкость
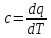
(1.4)
– это бесконечно
малое количество теплоты
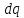 ,
,
необходимое для нагрева 1 кг вещества
на бесконечно малую величину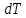 .
.
Факторы, влияющие на интенсивность теплоотдачи — Студопедия
На интенсивность теплоотдачи (при данном температурном напоре) влияют:
— природа возникновения движения;
— скорость и степень турбулентности набегающего потока;
— режим течения в пограничном слое;
— температура и физические свойства теплоносителя;
— форма, размеры и шероховатость поверхности обтекаемого тела и т.д.
Природа возникновения движения. Движение теплоносителя может быть вынужденным или свободным. Вынужденное движение возникает за счет внешних для данного процесса причин (движение летательного аппарата относительно воздуха; течение, обусловленное разностью давлений, создаваемой насосом, эжектором или компрессором, и др.). Свободным называется движение, возникающее за счет неоднородного распределения массовых сил в объеме теплоносителя вследствие разности плотностей холодных и горячих его частиц. Свободное движение называют также свободной конвекцией.
Степень турбулентности набегающего потока. Поток может быть турбулентным и до начала обтекания рассматриваемой поверхности, например, из-за наличия атмосферной турбулентности.
Степень турбулентности набегающего потока влияет на характер развития и структуру пограничного слоя (условия перехода ламинарного пограничного слоя в турбулентный и уровень турбулентности в турбулентном пограничном слое).
Физические свойства теплоносителя. Интенсивность конвективного теплообмена зависит от теплопроводности, теплоемкости, вязкости и плотности теплоносителя.
Влияние коэффициента теплопроводности l на интенсивность конвективного теплообмена связано прежде всего с ламинарной частью пограничного слоя, и особенно его пристенными слоями, где скорость потока близка к нулю и теплота передаётся в основном за счёт теплопроводности.
Влияние теплоёмкости с (для газов — cp) связано с тем, что при одинаковых условиях течения теплоноситель с большей теплоёмкостью переносит большее количество теплоты.
Вязкость теплоносителя оказывает влияние на толщину пограничного слоя и на интенсивность турбулентного перемешивания в нём. При прочих равных условиях увеличение вязкости приводит к образованию более толстого пограничного слоя и ухудшению перемешивания в нём. Вязкость газов и жидкостей характеризуют коэффициентом динамической вязкости m, Па×с и коэффициентом кинематической вязкостиn, м2/с, которые связаны соотношением 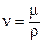 , где r, кг/м3 — плотность теплоносителя.
, где r, кг/м3 — плотность теплоносителя.
Коэффициент динамической вязкости зависит главным образом от природы теплоносителя и его температуры. У жидкостей значение m с увеличением температуры уменьшается, так как уменьшаются силы межмолекулярного взаимодействия, обусловливающие их вязкость. У газов, вязкость которых обусловлена беспорядочным тепловым движением молекул, коэффициент m с увеличением температуры возрастает. При умеренных давлениях его влиянием на коэффициент динамической вязкости можно пренебречь.
Коэффициент кинематический вязкости n также определяется природой теплоносителя. Вместе с тем при данном значении m его величина изменяется обратно пропорционально изменению плотности, которая у газов увеличивается с ростом давления и снижением температуры.
Влияние плотности теплоносителя r на конвективный теплообмен проявляется через изменения массового расхода теплоносителя и коэффициента кинематической вязкости. Например, уменьшение плотности воздуха с увеличением высоты полёта ведёт к росту кинематической вязкости n и, как следствие, к увеличению толщины пограничного слоя, что наряду со снижением расхода теплоносителя приводит к снижению интенсивности теплоотдачи.
Форма, размеры и шероховатость поверхности обтекаемого тела оказывают влияние на формирование пограничного слоя. Так, удобообтекаемые тела имеют более протяжённые участки пограничного слоя с ламинарным режимом течения, что снижает интенсивность теплообмена. Влияние шероховатости становится заметным только в турбулентном пограничном слое и при условии, что высота бугорков шероховатости превышает толщину вязкого подслоя.
ФОРМУЛА НЬЮТОНА
И. Ньютон установил, что плотность теплового потока между теплоносителем и омываемой им стенкой подчиняется соотношению
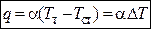 ,
,
где 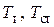 — температура соответственно теплоносителя и поверхности стенки. Разность
— температура соответственно теплоносителя и поверхности стенки. Разность 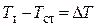 называется температурным напором, а коэффициент a, Вт/(м2×К) — коэффициентом теплоотдачи.Как видно, коэффициент теплоотдачи численно равен плотности теплового потока при температурном напоре в 1 К.
называется температурным напором, а коэффициент a, Вт/(м2×К) — коэффициентом теплоотдачи.Как видно, коэффициент теплоотдачи численно равен плотности теплового потока при температурном напоре в 1 К.
Поскольку интенсивность теплоотдачи неодинакова по всей поверхности обтекаемого тела, в практических расчётах различают местный aх (на расстоянии х от начала обтекаемой поверхности) и средний aср (по всей обтекаемой поверхности) коэффициенты теплоотдачи. Согласно формуле Ньютона местный коэффициент теплоотдачи на элементе площади dF равен 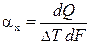 ,
,
где dQ — тепловой поток через элемент площади dF, а DТ — температурный напор на рассматриваемом участке.
Формула Ньютона не учитывает в явном виде всех факторов, влияющих на интенсивность процесса. Это влияние учитывает коэффициент теплоотдачи a, который зависит от тех же факторов, что и интенсивность конвективного теплообмена, т.е. от характера движения теплоносителя, его физических свойств, размера l и формы поверхности обтекаемого тела и т.д.: a = f (с, l, m, r, cp, l…).
Факторы, влияющие на цены на мазут
Почему цены на мазут колеблются?
- Спрос на мазут сезонный. Когда цены на сырую нефть стабильны, цены на мазут для дома имеют тенденцию расти в зимние месяцы с октября по март, когда спрос на мазут наиболее высок. Домовладелец на северо-востоке может использовать от 850 до 1200 галлонов топочного мазута в течение типичной зимы и потреблять очень мало в остальное время года.
- Стоимость замены сырой нефти. Стоимость сырой нефти является основным компонентом цены на топочный мазут. Мировой спрос и предложение определяют цены на сырую нефть. Спрос будет варьироваться в зависимости от таких факторов, как экономика и погода. На предложение могут влиять погодные явления в США и политические события в других странах. Количество нефти, производимой членами Организации стран-экспортеров нефти (ОПЕК), также может повлиять на мировые цены на сырую нефть.Посетите Что движет ценами на сырую нефть? Узнать больше.
- Конкуренция на местных рынках разная. Количество поставщиков топочного мазута в регионе может повлиять на уровень ценовой конкуренции в этом регионе. Цены на мазут и предложения услуг могут существенно различаться в регионах с небольшим количеством поставщиков по сравнению с районами, где имеется большое количество конкурирующих поставщиков. Потребители в сельской местности, где меньше конкурентов, могут платить более высокие цены за мазут.
- Операционные расходы по регионам могут отличаться. Стоимость доставки мазута в отдаленные места также может повлиять на цены на мазут. Стоимость ведения бизнеса может существенно различаться в зависимости от региона страны, в которой находится дилер.
Цены на мазут обычно соответствуют ценам на сырую нефть.
Что вызывает резкое повышение цен на мазут?
Цены на мазут для дома иногда могут резко возрасти, особенно в холодную погоду и зимние штормы.Большая система холодной погоды может повлиять на предложение, спрос и цены. Люди обычно потребляют больше топлива в то время, когда зимние бури прерывают работу систем доставки.
Увеличение потребления может уменьшить количество печного топлива в хранилищах намного быстрее, чем его можно будет пополнить, и нефтеперерабатывающие заводы могут оказаться не в состоянии удовлетворить спрос. Оптовые покупатели могут завышать цены на имеющийся товар, если они считают, что поставки недостаточны для удовлетворения краткосрочного потребительского спроса.
Например, на северо-востоке дополнительные поставки мазута могут поступать из других частей мира, таких как побережье Мексиканского залива или Европа.Транспортировка мазута из этих источников на северо-восток стоит дорого, и доставка может занять несколько недель. В течение этого времени складские запасы могут еще больше снизиться, беспокойство покупателей по поводу имеющегося краткосрочного предложения может возрасти, а цены могут вырасти — иногда резко — до тех пор, пока не появится новое предложение.
Последнее обновление: 23 октября 2019 г.
.
Удельная теплоемкость
цитировать книгу | author = Laider, Keith, J. | title = The World of Physical Chemistry | publisher = Oxford University Press | год = 1993 | id = ISBN 0-19-855919-4 ] Больше тепла энергия требуется для повышения температуры вещества с более высокой удельной теплоемкостью, чем вещества с низкой удельной теплоемкостью. Например, для повышения температуры слитка магния требуется в восемь раз больше тепловой энергии, чем требуется для свинцового слитка той же массы. Можно измерить удельную теплоемкость практически любого вещества, включая химические элементы, соединения, сплавы, растворы и композиты.
Символы для удельной теплоемкости: «C » или «c » в зависимости от того, как измеряется количество вещества (правила использования см. Ниже в разделе «Символы и стандарты»). При измерении физических свойств термин «специфический» означает, что мера представляет собой «объемное свойство» («интенсивное свойство)», в котором должно быть указано количество вещества. Например, тепловая энергия, необходимая для повышения температуры воды на один кельвин (равный одному градусу Цельсия), равна 4.184 джоуля на грамм — грамм — указанное количество. С научной точки зрения, эта мера может быть выражена как «c» = 4184 Дж кг –1 K –1 .
Основные показатели удельной теплоемкости
Количество единиц
При измерении удельной теплоемкости в науке и технике единица количества вещества часто выражается в массе: либо в граммах, либо в килограммах. являются единицей СИ. Однако, особенно в химии, единицей измерения удельной теплоемкости также может быть «моль», то есть определенное количество молекул или атомов.Когда единицей измерения является моль, термин «молярная теплоемкость » также может использоваться для более точного описания меры.
Температурный интервал
Температурный интервал в науке, технике и химии обычно составляет один кельвин или градус Цельсия (оба имеют одинаковую величину).
Другие единицы
В США другие единицы измерения удельной теплоемкости обычно используются в таких дисциплинах, как строительство и гражданское строительство.Здесь количество массы часто является фунтом-массой, единицей тепловой энергии является британская тепловая единица, а температурным интервалом является градус Фаренгейта.
Если температура выражается в естественных, а не исторических терминах, то есть как скорость увеличения энергии на единицу увеличения неопределенности состояния, тогда теплоемкость становится количеством битов взаимной информации между системой и окружающей средой, теряемых при двукратном увеличении абсолютной температуры [ П. Фраундорф (2003) [ http: // scitation.aip.org/getabs/servlet/GetabsServlet?prog=normal&id=AJPIAS000071000011001142000001&idtype=cvips&gifs=yes Теплоемкость в битах ], «Американский журнал физики» 71 : 11, 1142-1151. ([ http://arxiv.org/abs/cond-mat/9711074 arXiv: cond-mat / 9711074 ]) ]. Так, например, с каждым двукратным увеличением абсолютной температуры мы теряем 3/2 бита взаимной информации на атом в одноатомном идеальном газе.
Основные уравнения
* Уравнение, связывающее тепловую энергию с удельной теплоемкостью, где единичное количество выражается в массе: ::: Delta Q = mc Delta T: где Delta Q — тепловая энергия, вложенная или взятая вне вещества m — масса вещества, c — удельная теплоемкость, а Delta T — разность температур.
* Если единица измерения выражена в молях, уравнение, связывающее тепловую энергию с удельной теплоемкостью (также известное как «молярная теплоемкость»), выглядит следующим образом: Delta Q = nc Delta T: где Delta Q — положенная тепловая энергия. в или из вещества, n — число молей, c — удельная теплоемкость, а Delta T — разность температур.
Факторы, влияющие на удельную теплоемкость
* Степени свободы: Молекулы сильно отличаются от одноатомных газов, таких как гелий и аргон.В одноатомных газах тепловая энергия состоит только из «поступательных движений». Поступательные движения — это обычные движения всего тела в трехмерном пространстве, при которых частицы движутся и обмениваются энергией при столкновениях — как резиновые шарики в сильно встряхиваемом контейнере (см. Анимацию [ http://upload.wikimedia.org/wikipedia/commons/] 6 / 6d / Translational_motion.gifhere ]). Эти простые движения в трех измерениях пространства по осям X, Y и Z означают, что одноатомные атомы имеют три поступательные степени свободы.Однако молекулы обладают различными «внутренними» колебательными и вращательными степенями свободы, потому что они являются сложными объектами; они представляют собой совокупность атомов, которые могут перемещаться внутри молекулы по-разному (см. анимацию справа). Тепловая энергия сохраняется в этих внутренних движениях, но в расчете на один атом теплоемкость молекул не превышает теплоемкость одноатомных газов, если не задействованы колебательные моды.
Например, азот, который является двухатомной молекулой, имеет «пять» активных степеней свободы при комнатной температуре: три включают поступательное движение плюс две внутренние вращательные степени свободы.Хотя молярная теплоемкость при постоянном объеме азота при этой температуре составляет пять третей от молярной теплоемкости одноатомных газов в расчете на моль атомов, она составляет всего пять шестых от теплоемкости одноатомного газа, потому что каждый атом имеет меньше степеней свобода при низких температурах благодаря внутриатомной связи. Это ожидается, поскольку два атома азота имели бы шесть степеней свободы (по три для каждого атома), если бы они были свободны, но когда они соединены вместе, они теряют одну степень свободы, а вместе обладают только пятью.
Однако при более высоких температурах газообразный азот приобретает еще две степени внутренней свободы, поскольку молекула возбуждается в более высокие колебательные моды, которые накапливают тепловую энергию, и тогда теплоемкость на объем или моль молекул приближается к семи третям теплоемкости одноатомного атома. газы, или семь шестых одноатомных на основе моль атомов.Теперь это «более высокая» теплоемкость на атом, чем одноатомная фигура, потому что режим колебаний дает дополнительную степень свободы «потенциальной энергии» на пару атомов, которой одноатомные газы не могут обладать. [ Сравнение должно проводиться в условиях постоянного объема — «C v H» — так, чтобы никакая работа не выполнялась. «C v H» азота «C v H» (100 кПа, 20 ° C) = 20,8 Дж моль –1 K –1 по сравнению с одноатомными газами, которые равны 12,4717 Дж моль –1 K –1 .Цитирование: [ http://www.whfreeman.com/ W.H. Freeman’s ] «Физическая химия», часть 3: изменение ([ http://www.whfreeman.com/college/pdfs/pchem8e/PC8eC21.pdf 422 kB PDF, здесь ]), упражнение 21.20b, Стр. 787. Также [ http://www.gsu.edu/ Университета штата Джорджия] «[ http://hyperphysics.phy-astr.gsu.edu/hbase/kinetic/shegas.html Молярная удельная теплота Газов ] ». ] См. «Термодинамическая температура» для получения дополнительной информации о поступательных движениях, кинетической (тепловой) энергии и их связи с температурой.
* На моль молекул: Когда измеряется удельная теплоемкость «c» материала (строчная буква «c» означает, что единица измерения выражается в массе), возникают разные значения, потому что разные вещества имеют разные « молярные массы »(по сути, масса отдельных атомов или молекул). Отчасти тепловая энергия возникает из-за «количества» колеблющихся атомов или молекул. Если у вещества более легкая молярная масса, то каждый грамм этого вещества содержит больше атомов или молекул, способных накапливать тепловую энергию.Вот почему водород — самое легкое из существующих веществ — имеет такую высокую удельную теплоемкость в граммах; в одном грамме его содержится в два раза больше молекул, чем в грамме гелия, а для других веществ соотношение еще больше. Однако, если удельная теплоемкость измеряется на «молярной» основе (заглавная буква «C)», различия между веществами менее выражены, а молярная теплоемкость водорода незначительна.
* На моль атомов: И наоборот, для веществ «на молекулярной основе» (которые также поглощают тепло в своих внутренних степенях свободы) массивные, сложные молекулы с большим атомным числом — например, бензин — могут хранить большое количество энергии. энергии на моль, и все же они совершенно ничем не примечательны на основе массы или на основе атома.Это происходит потому, что в полностью возбужденных системах тепло накапливается независимо каждым атомом вещества, а не главным образом за счет движения молекул в объеме.
Таким образом, именно теплоемкость на моль атомов, а не на моль молекул, ближе всего к постоянной величине для всех веществ при высоких температурах. По этой причине при сравнении удельной теплоемкости молекулярных твердых тел и газов следует проявлять некоторую осторожность при указании базиса моль молекул по сравнению с основанием моль атомов. Идеальные газы имеют одинаковое количество молекул в объеме, поэтому увеличение молекулярной сложности увеличивает теплоемкость в расчете на объем и на моль молекул, но может понижать или повышать теплоемкость на основе каждого атома, в зависимости от того, температура достаточна для хранения энергии в виде атомной вибрации.
В твердых телах предел теплоемкости обычно составляет около 3R на моль атомов, поскольку каждому атому доступно 6 степеней свободы (3 кинетических и 3 потенциальных), и каждая из этих степеней вносит удельную теплоемкость R / 2 на моль атомов. Для одноатомных газов удельная теплоемкость составляет только половину от этой (3R / 2 на моль) из-за потери всех степеней свободы потенциальной энергии. Для многоатомных газов теплоемкость будет промежуточной между этими значениями на основе на моль атомов, и (для термостабильных молекул) будет приближаться к пределу 3R на моль атомов для газов, состоящих из сложных молекул со всеми колебательные моды возбуждены.Это связано с тем, что сложные молекулы газа можно рассматривать как большие блоки вещества, которые потеряли лишь небольшую долю степеней свободы по сравнению с полностью интегрированным твердым телом.
Соответствие этим соображениям для твердых тел : Начиная с , объемная плотность твердого химического элемента сильно связана с его молярной массой, вообще говоря, существует сильная обратная корреляция между плотностью твердого тела и его «c p «(удельная теплоемкость при постоянном давлении в пересчете на массу).Большие слитки твердых тел низкой плотности, как правило, поглощают больше тепловой энергии, чем маленькие плотные слитки той же массы, потому что первые обычно имеют больше атомов. Таким образом, вообще говоря, существует тесная корреляция между «размером» твердого химического элемента и его общей теплоемкостью (см. «Объемная теплоемкость)». Однако есть много отклонений от общей тенденции. Например, мышьяк, который всего на 14,5% менее плотен, чем сурьма, имеет почти на 59% большую удельную теплоемкость в пересчете на массу.Другими словами; хотя слиток мышьяка всего на 17% больше, чем слиток сурьмы такой же массы, он поглощает на 59% больше тепловой энергии при заданном повышении температуры.
Другие факторы
* Водородные связи: Водородсодержащие полярные молекулы, такие как этанол, аммиак и вода, в жидкой фазе имеют мощные межмолекулярные «водородные связи». Эти связи обеспечивают еще одно место, где тепловая энергия может храниться в виде потенциальной энергии вибрации даже при сравнительно низких температурах.Водородные связи объясняют тот факт, что жидкая вода хранит почти теоретический предел 3R на моль атомов даже при относительно низких температурах (то есть около точки замерзания воды).
* Примеси: В случае сплавов существует несколько условий, при которых небольшие концентрации примесей могут сильно влиять на удельную теплоемкость. Сплавы могут демонстрировать заметное различие в поведении даже в том случае, если небольшое количество примесей является одним из элементов сплава; например, примеси в полупроводниковых ферромагнитных сплавах могут приводить к совершенно другим свойствам теплоемкости, как впервые предсказали Уайт и Хоган.[ [http://prola.aps.org/abstract/PR/v188/i2/p870_1 С. Майкл Хоган, (1969) «Плотность состояний изоляционного ферромагнитного сплава» Phys. Ред. 188, 870 — 874, [Выпуск 2 — декабрь 1969] ]
символы и стандарты
Когда масса является единицей измерения, символ удельной теплоемкости — строчная буква «c». Когда моль — это единица измерения, обозначается заглавная буква «C». В качестве альтернативы — особенно в химии, а не в инженерии — версия в верхнем регистре для удельной теплоемкости «C» может использоваться в сочетании с суффиксом, представляющим «энтальпию» (символ: либо «H», либо «h)»; в частности, когда моль является единицей измерения, суффикс энтальпии — это прописная буква «H», а когда масса — это единичная величина, суффикс является строчной буквой «h».
Современные единицы СИ для измерения удельной теплоемкости — это либо «джоуль на грамм-кельвин» (Jg –1 K –1 ), либо «джоуль на моль-кельвин» (Джмоль –1 K ). –1 ). Различные префиксы СИ могут создавать вариации этих единиц (например, кДжкг –1 K –1 и кДжмоль –1 K –1 ). Для альтернативных единиц используются следующие символы: фунты-масса (символ: фунты) для количества, калории (символ: кал) и британские тепловые единицы (символ: БТЕ) для энергии и градусы Фаренгейта (символ: ° F) для увеличения температура.
Существуют два совершенно разных экспериментальных условия, при которых измеряется удельная теплоемкость, и они обозначаются индексом в нижнем индексе, изменяющим символы «C» или «c». Удельную теплоемкость веществ обычно измеряют при постоянном давлении (символы: «C p » или «c p »). Однако жидкости (газы и жидкости) обычно также измеряются при постоянном объеме (символы: «C v » или «c v »). Измерения при постоянном давлении дают более высокие значения, чем измерения при постоянном объеме, потому что работа должна выполняться в первом случае.Эта разница особенно велика для газов, где значения при постоянном давлении обычно на 30–66,7% больше, чем при постоянном объеме.
Таким образом, символы для удельной теплоемкости следующие:
Выводы теплоемкости и удельной теплоемкости
Определение теплоемкости
Теплоемкость математически определяется как отношение небольшого количества тепла. «δQ» добавлено к телу к соответствующему небольшому увеличению его температуры «dT»:
: C = left (frac {delta Q} {dT}
ight) _ {cond.} = T left (frac {d S} {d T}
ight) _ {cond.}
Для термодинамических систем с более чем одним физическим измерением приведенное выше определение не дает единственной уникальной величины, если не определен конкретный бесконечно малый путь через фазовое пространство системы (это означает, что необходимо всегда знать, где находятся все части системы, какая у них масса и с какой скоростью они движутся). Эта информация используется для учета различных способов хранения тепла в виде кинетической энергии (энергии движения) и потенциальной энергии (энергии, хранящейся в силовых полях), когда объект расширяется или сжимается.Для всех реальных систем путь этих изменений должен быть явно определен, так как значение теплоемкости зависит от того, какой путь от одной температуры к другой выбран. Особенно полезными в этом контексте являются значения теплоемкости для постоянного объема «C V » и постоянного давления «C P ». Они будут определены ниже.
Теплоемкость сжимаемых тел
Состояние простого сжимаемого тела с фиксированной массой описывается двумя термодинамическими параметрами, такими как температура «T» и давление «p».Следовательно, как упоминалось выше, можно различать «теплоемкость при постоянном объеме», C_V, и «теплоемкость при постоянном давлении», C_p:
: C_V = left (frac {delta Q} {dT}
ight) _V = Tleft (гидроразрыв {частичный S} {частичный T}
ight) _V: C_p = left (frac {delta Q} {dT}
ight) _p = Tleft (frac {частичный S} {частичный T}
ight) _p
где: дельта Q — бесконечно малое количество добавленного тепла,: dT — последующее повышение температуры.
Прирост внутренней энергии — это добавленное тепло и добавленная работа: dU = T, dS-p, dV
Таким образом, теплоемкость при постоянном объеме равна: C_V = left (frac {partial U} {partial T}
ight) _V
Энтальпия определяется как H = U + PV.Приращение энтальпии равно: dH = dU + (pdV + Vdp)! которая после замены dU на приведенное выше уравнение и исключения членов PdV сводится к :: dH = T, dS + V, dp.
Таким образом, теплоемкость при постоянном давлении равна: C_p = left (frac {partial H} {partial T}
ight) _p.
Обратите внимание, что это последнее «определение» несколько круговое, поскольку само понятие «энтальпия» было «изобретено» как мера тепла, поглощаемого или производимого при постоянном давлении (условиях, в которых обычно работают химики). Таким образом, энтальпия просто учитывает дополнительное тепло, которое производится или поглощается работой объемно-давление при постоянном давлении.Таким образом, неудивительно, что теплоемкость при постоянном давлении может быть определена в терминах энтальпии, поскольку «энтальпия» была определена в первую очередь для этого.
Связь между удельной теплоемкостью
Измерение теплоемкости при постоянном объеме может быть чрезвычайно трудным для жидкостей и твердых тел. То есть небольшие изменения температуры обычно требуют больших давлений для поддержания постоянного объема жидкости или твердого вещества, подразумевая, что содержащий сосуд должен быть почти жестким или, по крайней мере, очень прочным (см. Коэффициент теплового расширения и сжимаемости).2 T} {
ho eta_T}, где: alpha — коэффициент теплового расширения, и: eta_T — изотермическая сжимаемость. Здесь приведен вывод. Для идеального газа это сводится к простому соотношению: c_p — c_v = nR !, где n — число молей, а c_p и c_v — экстенсивные (немолярные) свойства.
Удельная теплоемкость
Удельная теплоемкость материала составляет
: c = {частичное C относительно частичного m},
, что в отсутствие фазовых переходов эквивалентно
: c = E_ m = {C над m} = {C над {
ho V,
где: C — теплоемкость тела, сделанного из рассматриваемого материала,: m — масса тела,: V — объем тела, и:
ho = frac {m} {V} — плотность материала.
Для газов, а также для других материалов, находящихся под высоким давлением, необходимо различать различные граничные условия для рассматриваемых процессов (поскольку значения существенно различаются в зависимости от условий). Типичные процессы, для которых может быть определена теплоемкость, включают изобарические (постоянное давление, dp = 0) или изохорные (постоянный объем, dV = 0) процессы. Соответствующие удельные теплоемкости выражаются как
: c_p = left (frac {partial C} {partial m}
ight) _p,: c_V = left (frac {частичный C} {частичный m}
ight) _V.{-1} ,, объемная теплоемкость. В инженерной практике c_V для твердых тел или жидкостей часто означает объемную теплоемкость, а не постоянный объем. В таких случаях удельная теплоемкость (удельная теплоемкость) часто явно записывается с нижним индексом m, как c_m ,. Конечно, из приведенных выше соотношений для твердых тел записывают
: c_m = frac {C} {m} = frac {c_V} {
хо}.
Безразмерная теплоемкость
«Безразмерная теплоемкость» материала равна: C ^ * = {C over nR} = {C over {Nk, где: «C» — теплоемкость тела, сделанного из материала. рассматриваемый (Дж · K −1 ): «n» — количество вещества в теле (моль): «R» — газовая постоянная (Дж · K -1 · моль -1 ): «nR = Nk» — это количество вещества в теле ( -1 Дж · К): «N» — количество молекул в теле.(безразмерный): «k» — постоянная Больцмана (Дж · К -1 · молекула -1 )
Опять же, единицы СИ показаны для примера.
Теоретические модели
Газовая фаза
Удельную теплоемкость газа лучше всего представить в терминах степеней свободы отдельной молекулы. Разные степени свободы соответствуют различным способам хранения энергии в молекуле. Молекула может накапливать энергию в своем поступательном движении по формуле:
: E = frac {1} {2}, mleft (v_x ^ 2 + v_y ^ 2 + v_z ^ 2
ight)
где «m» — масса молекулы, а [v_x, v_y, v_z] — скорость центра масс молекулы.2
ight)
где «I» — тензор момента инерции молекулы, а [omega_1, omega_2, omega_3] — псевдовектор угловой скорости (в системе координат, совмещенной с главными осями молекулы). В общем, тогда будет три дополнительных степени свободы, соответствующих вращательному движению молекулы (для линейных молекул один из членов тензора инерции обращается в нуль, и есть только две вращательные степени свободы). Степени свободы, соответствующие сдвигам и поворотам, называются «жесткими» степенями свободы, поскольку они не связаны с деформацией молекулы.
Движения атомов в молекуле, которые не являются частью ее грубого поступательного движения или вращения, можно классифицировать как колебательные движения. Можно показать, что если в молекуле есть «n» атомов, то будет до 3n-3-n_r колебательных степеней свободы, где n_r — количество вращательных степеней свободы. Фактическое количество может быть меньше из-за различной симметрии.
Если бы молекулу можно было полностью описать с помощью классической механики, то мы могли бы использовать теорему о равнораспределении энергии, чтобы предсказать, что каждая степень свободы будет иметь среднюю энергию в размере (1/2) «kT», где «k «- постоянная Больцмана, а» T «- температура.Наш расчет теплосодержания будет простым. Каждая молекула будет удерживать в среднем энергию («f» / 2) «kT», где «f» — общее количество степеней свободы в молекуле. Полная внутренняя энергия газа будет («f» / 2) «NkT», где «N» — общее количество молекул. Тогда теплоемкость (при постоянном объеме) будет постоянной («f /» 2) «Nk», удельная теплоемкость будет («f» / 2) «k», а безразмерная теплоемкость будет просто «f «/ 2.
Обычно нельзя считать, что различные степени свободы подчиняются классической механике.Классически считается, что энергия каждой степени свободы непрерывна — она может принимать любое положительное значение в зависимости от температуры. В действительности количество энергии, которое может находиться в определенной степени свободы, квантуется: оно может увеличиваться и уменьшаться только в конечных количествах. Хорошей оценкой размера этого минимального количества является энергия первого возбужденного состояния этой степени свободы над его основным состоянием. Например, первое колебательное состояние молекулы HCl имеет энергию около 5.74 × 10 –20 джоуль. Если бы это количество энергии было вложено в классическую степень свободы, это соответствовало бы температуре около 4156 K.
Если бы температура вещества была настолько низкой, что энергия равнораспределения (1/2) «kT» была намного меньше, чем эта энергия возбуждения, тогда в этой степени свободы будет мало или совсем не будет энергии. Эта степень свободы затем называется «вымороженной». Как упоминалось выше, температура, соответствующая первому возбужденному колебательному состоянию HCl, составляет около 4156 К.При температурах значительно ниже этого значения колебательные степени свободы молекулы HCL будут заморожены. Они будут содержать мало энергии и не будут влиять на теплосодержание газообразного HCl.
Видно, что для каждой степени свободы существует критическая температура, при которой степень свободы «размораживается» и начинает принимать энергию классическим способом. В случае поступательных степеней свободы эта температура — это температура, при которой тепловая длина волны молекул примерно равна размеру контейнера.Для контейнера макроскопического размера (например, 10 см) эта температура чрезвычайно мала и не имеет значения, поскольку газ обязательно сжижается или замерзает до того, как будет достигнута эта низкая температура. Для любого реального газа мы можем считать, что поступательные степени свободы всегда являются классическими и содержат среднюю энергию «(3/2) kT» на молекулу.
Вращательные степени свободы — это следующие за «разморозкой»: в двухатомном газе, например, критическая температура для этого перехода обычно составляет несколько десятков кельвинов.Наконец, колебательные степени свободы обычно размораживаются в последнюю очередь. Например, для двухатомных газов критическая температура колебательного движения обычно составляет несколько тысяч кельвинов.
Следует отметить, что предполагалось, что атомы не имеют вращательных или внутренних степеней свободы. На самом деле это неправда. Например, атомные электроны могут существовать в возбужденных состояниях, и даже атомное ядро может иметь возбужденные состояния. Предполагается, что каждая из этих внутренних степеней свободы заморожена из-за их относительно высокой энергии возбуждения.Тем не менее, при достаточно высоких температурах пренебрегать этими степенями свободы нельзя.
Одноатомный газ
В случае одноатомного газа, такого как гелий, при постоянном объеме, если предположить, что не происходит электронных или ядерных квантовых возбуждений, каждый атом в газе имеет только 3 степени свободы, все из которых являются поступательными. тип. Никакая энергетическая зависимость не связана со степенями свободы, определяющими положение атомов. В то время как на самом деле степени свободы, соответствующие импульсам атомов, являются квадратичными и, таким образом, вносят вклад в теплоемкость.Есть «N» атомов, каждый из которых имеет 3 компонента импульса, что приводит к 3 «N» полным степеням свободы. Это дает:
: C_V = left (frac {частичный U} {частичный T}
ight) _V = frac {3} {2} N, k_B = frac {3} {2} n, R
: C_ {V, m} = frac {C_V} {n} = frac {3} {2} R = 1,5 R
, где
: C_V — «теплоемкость» при постоянном объеме газа: C_ {V, m} — «молярная теплоемкость» при постоянном объеме газа: «N» — это общая количество атомов, присутствующих в контейнере: «n» — это количество молей атомов, присутствующих в контейнере («n» — это соотношение «N» и числа Авогадро): «R» — идеальная газовая постоянная, (8.314570 [70] J K -1 моль -1 ). «R» равно произведению постоянной Больцмана k_B и числа Авогадро
В следующей таблице показаны экспериментальные измерения молярной теплоемкости постоянного объема, сделанные для каждого благородного одноатомного газа (при 1 атм и 25 ° C):
Это очевидно из Из таблицы видно, что экспериментальные теплоемкости одноатомных благородных газов в очень высокой степени согласуются с этим простым применением статистической механики.
Двухатомный газ
В несколько более сложном случае идеального газа, состоящего из двухатомных молекул, наличие внутренних степеней свободы очевидно.Помимо трех поступательных степеней свободы, существуют вращательные и колебательные степени свободы. В общем, число степеней свободы «f» в молекуле с атомами «n a » равно 3 «n a »:
: f = 3n_a,
Математически всего имеется три степени свободы вращения, одна из которых соответствует вращению вокруг каждой из осей трехмерного пространства. Однако на практике мы будем рассматривать только существование двух степеней свободы вращения для линейных молекул.Это приближение справедливо, потому что момент инерции относительно межъядерной оси исчезающе мал по сравнению с другими моментами инерции в молекуле (это происходит из-за чрезвычайно малых радиусов атомных ядер по сравнению с расстоянием между ними в молекуле). Квантово-механически можно показать, что интервал между последовательными собственными состояниями вращательной энергии обратно пропорционален моменту инерции относительно этой оси. Поскольку момент инерции вокруг межъядерной оси исчезающе мал по сравнению с двумя другими осями вращения, энергетический интервал можно считать настолько большим, что возбуждение вращательного состояния не может произойти, если только температура не будет чрезвычайно высокой.Мы можем легко вычислить ожидаемое количество колебательных степеней свободы (или колебательных мод). Есть три степени свободы поступательного движения и две степени свободы вращения, поэтому
: f_mathrm {vib} = f-f_mathrm {trans} -f_mathrm {rot} = 6-3-2 = 1,
Каждая вращательная и поступательная степень свободы вносит вклад «R» / 2 в общую молярную теплоемкость газа. Однако каждая колебательная мода будет давать вклад R в общую молярную теплоемкость. Это связано с тем, что для каждой колебательной моды существует потенциальная и кинетическая составляющие энергии.И потенциальная, и кинетическая составляющие будут вносить вклад «R» / 2 в общую молярную теплоемкость газа. Следовательно, мы ожидаем, что двухатомная молекула будет иметь молярную теплоемкость при постоянном объеме
: C_ {V, m} = frac {3R} {2} + R + R = frac {7R} {2} = 3,5 R
, где термины происходят от поступательной, вращательной и колебательной степеней свободы соответственно.
Ниже приводится таблица некоторых молярных теплоемкостей при постоянном объеме различных двухатомных газов.
Из приведенной выше таблицы ясно, что существует проблема с приведенной выше теорией.У всех исследованных диатомовых водоемов теплоемкость ниже, чем предсказывается теоремой о равнораспределении, за исключением Br 2 . Однако по мере того, как атомы, составляющие молекулы, становятся тяжелее, теплоемкость приближается к ожидаемым значениям. Одна из причин этого явления — квантование колебательных и, в меньшей степени, вращательных состояний. Фактически, если предположить, что молекулы остаются в своем низкоэнергетическом колебательном состоянии из-за больших расстояний между уровнями энергии, прогнозируемая молярная теплоемкость постоянного объема для двухатомной молекулы становится
: C_ {V, m} = frac {3R} {2} + R = гидроразрыв {5R} {2} = 2.5R
, что является довольно близким приближением к теплоемкости более легких молекул в приведенной выше таблице. Если сделать приближение квантового гармонического осциллятора, то окажется, что расстояния между уровнями квантовой колебательной энергии на самом деле обратно пропорциональны квадратному корню из приведенной массы атомов, составляющих двухатомную молекулу. Следовательно, в случае более тяжелых двухатомных молекул расстояния между квантовыми колебательными уровнями энергии становятся меньше, что допускает большее количество возбуждений на более высокие колебательные уровни при фиксированной температуре.
Другие газы
Таким образом, теплоемкость идеального газа с f степенями свободы определяется как
: C_ {V, m} = frac {f} {2} R
Это уравнение также применимо многоатомным газам, если известны степени свободы.
Олидная фаза
Для вещества в кристаллической твердой фазе закон Дюлонга-Пети, который был обнаружен эмпирически, гласит, что удельная мольная теплоемкость принимает значение 3 R. Действительно, для твердых металлических химических элементов при комнатной температуре температура, молярные теплоемкости колеблются примерно от 2.От 8 R до 3,4 R (заметным исключением является бериллий при 2,0 R).
Теоретическая максимальная теплоемкость для все больших и больших многоатомных газов при более высоких температурах также приближается к пределу Дюлонга-Пети в 3 R, если она рассчитывается на моль атомов, а не молекул. Причина в том, что газы с очень большими молекулами теоретически обладают почти такой же высокотемпературной теплоемкостью, что и твердые тела, при этом отсутствует только (небольшой) вклад теплоемкости, который исходит от потенциальной энергии, которая не может храниться между отдельными молекулами в газе.
«Предел» Дюлонга-Пети вытекает из теоремы о равнораспределении и, как таковой, действителен только в классическом пределе континуума микросостояний, который является пределом высокой температуры. Для легких и неметаллических элементов, а также для большинства обычных молекулярных твердых веществ на основе углеродных соединений при стандартной температуре окружающей среды квантовые эффекты также могут играть важную роль, как и в многоатомных газах. Эти эффекты обычно в совокупности дают теплоемкость ниже 3 R на моль «атомов» в твердом теле, хотя теплоемкость, рассчитанная «на моль молекул» в молекулярных твердых телах, может быть больше 3 R.Например, теплоемкость водяного льда при температуре плавления составляет около 4,6 R на моль молекул, но только 1,5 R на моль атомов. Меньшее число является результатом «вымораживания» возможных мод колебаний для легких атомов при достаточно низких температурах, как и во многих газах. Эти эффекты наблюдаются в твердых телах чаще, чем в жидкостях: например, теплоемкость жидкой воды снова близка к теоретическим 3 R на моль атомов теоретического максимума Дюлонга-Пети.
Для более современного и точного анализа теплоемкости твердых тел, особенно при низких температурах, полезно использовать идею фононов.{T_f} C (T), гидроразрыв {dT} {T}.
Теплоемкость должна быть равна нулю при нулевой температуре, чтобы указанный выше интеграл не давал бесконечной абсолютной энтропии, нарушая, таким образом, третий закон термодинамики. Одна из сильных сторон модели Дебая состоит в том, что (в отличие от предыдущей модели Эйнштейна) она предсказывает приближение теплоемкости к нулю при приближении к нулю температуры, а также предсказывает правильную математическую форму этого подхода.
См. Также
* Теплота
* Коэффициент теплоемкости
* Уравнение теплопроводности
* Коэффициент теплопередачи
* Скрытая теплота
* Метод соединения (оценка теплоемкостей)
* Удельная теплота плавления
* Удельная теплота парообразования
* Температура
* Термодинамическая (абсолютная) температура
* Объемная теплоемкость
Ссылки
Внешние ссылки
* [ http: // www.ultraheat.com Нагреватели образцов ]
.
