Гидравлический расчет разветвленного трубопровода: Самостоятельный гидравлический расчет трубопровода
Гидравлический расчет трубопроводов в Excel
Опубликовано 08 Апр 2014
Рубрика: Теплотехника | 56 комментариев
Системы отопления зданий, теплотрассы, водопроводы, системы водоотведения, гидравлические схемы станков, машин – все это примеры систем, состоящих из трубопроводов. Гидравлический расчет трубопроводов — особенно сложных, разветвленных…
… — является очень непростой и громоздкой задачей. Сегодня в век компьютеров решать ее стало существенно легче при использовании специального программного обеспечения. Но хорошие специальные программы дорого стоят и есть они, как правило, только у специалистов-гидравликов.
В этой статье мы рассмотрим гидравлический расчет трубопроводов на примере расчета в Excel горизонтального участка трубопровода постоянного диаметра по двум методикам и сравним полученные результаты. Для «неспециалистов» применение представленной ниже программы позволит решить несложные «житейские» и производственные задачи. Для специалистов применение этих расчетов возможно в качестве проверочных или для выполнения быстрых простых оценок.
Как правило, гидравлический расчет трубопроводов включает в себя решение двух задач:
1. При проектировочном расчете требуется по известному расходу жидкости найти потери давления на рассматриваемом участке трубопровода. (Потери давления – это разность давлений между точкой входа и точкой выхода.)
2. При проверочном расчете (при аудите действующих систем) требуется по известному перепаду давления (разность показаний манометров на входе в трубопровод и на выходе) рассчитать расход жидкости, проходящей через трубопровод.
Приступаем к решению первой задачи. Решить вторую задачу вы сможете легко сами, используя сервис программы MS Excel «Подбор параметра». О том, как использовать этот сервис, подробно описано во второй половине статьи «Трансцендентные уравнения? «Подбор параметра» в Excel!».
Предложенные далее расчеты в Excel, можно выполнить также в программе OOo Calc из свободно распространяемого пакета Open Office.
Правила цветового форматирования ячеек листа Excel, которые применены в статьях этого блога, детально описаны на странице «О блоге».
Расчет в Excel трубопроводов по формулам теоретической гидравлики.
Рассмотрим порядок и формулы расчета в Excel на примере прямого горизонтального трубопровода длиной 100 метров из трубы ø108 мм с толщиной стенки 4 мм.
Исходные данные:
1. Расход воды через трубопровод G в т/час вводим
в ячейку D4: 45,000
2. Температуру воды на входе в расчетный участок трубопровода tвх в °C заносим
в ячейку D5: 95,0
3. Температуру воды на выходе из расчетного участка трубопровода tвых в °C записываем
в ячейку D6: 70,0
4. Внутренний диаметр трубопровода d в мм вписываем
в ячейку D7: 100,0
5. Длину трубопровода L в м записываем
в ячейку D8: 100,000
6. Эквивалентную шероховатость внутренних поверхностей труб ∆ в мм вносим
в ячейку D9: 1,000
Выбранное значение эквивалентной шероховатости соответствует стальным старым заржавевшим трубам, находящимся в эксплуатации много лет.
Эквивалентные шероховатости для других типов и состояний труб приведены на листе «Справка» расчетного файла Excel «gidravlicheskiy-raschet-truboprovodov.xls», ссылка на скачивание которого дана в конце статьи.
7. Сумму коэффициентов местных сопротивлений Σ(ξ) вписываем
в ячейку D10: 1,89
Мы рассматриваем пример, в котором местные сопротивления присутствуют в виде стыковых сварных швов (9 труб, 8 стыков).
Для ряда основных типов местных сопротивлений данные и формулы расчета представлены на листах «Расчет коэффициентов» и «Справка» файла Excel «gidravlicheskiy-raschet-truboprovodov.xls».
Результаты расчетов:
8. Среднюю температуру воды tср в °C вычисляем
в ячейке D12: =(D5+D6)/2 =82,5
tср=(tвх+tвых)/2
9. Кинематический коэффициент вязкости воды n в cм2/с при температуре tср рассчитываем
в ячейке D13: =0,0178/(1+0,0337*D12+0,000221*D12^2) =0,003368
n=0,0178/(1+0,0337*tср+0,000221*tср2)
10. Среднюю плотность воды ρ в т/м3 при температуре tср вычисляем
в ячейке D14: =(-0,003*D12^2-0,1511*D12+1003,1)/1000 =0,970
ρ=(-0,003*tср2-0,1511*tср+1003, 1)/1000
11. Расход воды через трубопровод G’ в л/мин пересчитываем
в ячейке D15: =D4/D14/60*1000 =773,024
G’=G*1000/(ρ*60)
Этот параметр пересчитан нами в других единицах измерения для облегчения восприятия величины расхода.
12. Скорость воды в трубопроводе v в м/с вычисляем
в ячейке D16: =4*D4/D14/ПИ()/(D7/1000)^2/3600 =1,640
v=4*G/(ρ*π*(d/1000)2*3600)
К ячейке D16 применено условное форматирование. Если значение скорости не попадает в диапазон 0,25…1,5 м/с, то фон ячейки становится красным, а шрифт белым.
Предельные скорости движения воды приведены на листе «Справка» расчетного файла Excel «gidravlicheskiy-raschet-truboprovodov.xls».
13. Число Рейнольдса Re определяем
в ячейке D17: =D16*D7/D13*10 =487001,4
Re=v*d*10/n
14. Коэффициент гидравлического трения λ рассчитываем
в ячейке D18: =ЕСЛИ(D17<=2320;64/D17;ЕСЛИ(D17<=4000; 0,0000147*D17;0,11* (68/D17+D9/D7)^0,25)) =0,035
λ=64/Re при Re≤2320
λ=0,0000147*Re при 2320≤Re≤4000
λ=0,11*(68/Re+∆/d)0,25 при Re≥4000
15. Удельные потери давления на трение R в кг/(см2*м) вычисляем
в ячейке D19: =D18*D16^2*D14/2/9,81/D7*100 =0,004645
R=λ*v2*ρ*100/(2*9,81*d)
16. Потери давления на трение dPтр в кг/см2 и Па находим соответственно
в ячейке D20: =D19*D8 =0,464485
dPтр=R*L
и в ячейке D21: =D20*9,81*10000 =45565,9
dPтр=dPтр*9,81*10000
17. Потери давления в местных сопротивлениях dPмс в кг/см2 и Па находим соответственно
в ячейке D22: =D10*D16^2*D14*1000/2/9,81/10000 =0,025150
dPмс=Σ(ξ)*v2*ρ/(2*9,81*10)
и в ячейке D23: =D22*9,81*10000 =2467,2
dPтр=dPмс*9,81*10000
18. Расчетные потери давления в трубопроводе dP в кг/см2 и Па находим соответственно
в ячейке D24: =D20+D22 =0,489634
dP=dPтр+dPмс
и в ячейке D25: =D24*9,81*10000 =48033,1
dP=dP*9,81*10000
19. Характеристику гидравлического сопротивления трубопровода S в Па/(т/ч)2 вычисляем
в ячейке D26: =D25/D4^2 =23,720
S=dP/G2
Гидравлический расчет в Excel трубопровода по формулам теоретической гидравлики выполнен!
Гидравлический расчет трубопроводов в Excel по формулам СНиП 2.04.02-84.
Этот расчет определяет потери на трение в трубопроводах по эмпирическим формулам без учета коэффициентов местных сопротивлений, но с учетом сопротивлений, вносимых стыками.
На длинных трубопроводах, каковыми являются водопроводы и теплотрассы, влияние местных сопротивлений мало по сравнению с шероховатостью стенок труб и перепадами высот, и часто коэффициентами местных сопротивлений можно пренебречь при оценочных расчетах.
Исходные данные:
Этот расчет использует ранее введенные в предыдущем расчете значения внутреннего диаметра трубопровода d и длины трубопровода L, а также рассчитанное значение скорости движения воды v.
1. Выбираем из выпадающего списка, расположенного над ячейками A30…E30 вид трубы:
Неновые стальные и неновые чугунные без внутр. защитного покр. или с битумным защитным покр., v > 1,2м/c
Результаты расчетов:
По выбранному виду трубы Excel автоматически извлекает из таблицы базы данных значения эмпирических коэффициентов. Таблица базы данных, взятая из СНиП 2.04.02–84, расположена на этом же рабочем листе «РАСЧЕТ».
2. Коэффициент m извлекается
в ячейку D32: =ИНДЕКС(h41:h52;h39) =0,300
3. Коэффициент A0 извлекается
в ячейку D33: =ИНДЕКС(I31:I42;I29) =1,000
4. Коэффициент 1000A1 извлекается
в ячейку D34: =ИНДЕКС(J31:J42;J29) =21,000
5. Коэффициент 1000A1/(2g) извлекается
в ячейку D35: =ИНДЕКС(K31:K42;K29) =1,070
6. Коэффициент С извлекается
в ячейку D36: =ИНДЕКС(L31:L42;L29) =0,000
7. Коэффициент гидравлического сопротивления i в м.вод.ст./м рассчитываем
в ячейке D37: =D35/1000*((D33+D36/D16)^D32)/((D7/1000)^(D32+1))*D16^2 =0,057
i=((1000A1/(2g))/1000)*(((A0+C/v)m)/((d/1000)(m+1)))*v2
8. Расчетные потери давления в трубопроводе dP в кг/см2 и Па находим соответственно
в ячейке D38: =D39/9,81/10000 =0,574497
dP=dP/9,81/10000
и в ячейке D39: =D37*9,81*1000*D8 =56358,1
dP=i*9,81*1000*L
Гидравлический расчет трубопровода по формулам Приложения 10 СНиП 2.04.02–84 в Excel завершен!
Итоги.
Полученные значения потерь давления в трубопроводе, рассчитанные по двум методикам отличаются в нашем примере на 15…17%! Рассмотрев другие примеры, вы можете увидеть, что отличие иногда достигает и 50%! При этом значения, полученные по формулам теоретической гидравлики всегда меньше, чем результаты по СНиП 2.04.02–84. Я склонен считать, что точнее первый расчет, а СНиП 2.04.02–84 «подстраховывается». Возможно, я ошибаюсь в выводах. Следует отметить, что гидравлические расчеты трубопроводов тяжело поддаются точному математическому моделированию и базируются в основном на зависимостях, полученных из опытов.
В любом случае, имея два результата, легче принять нужное правильное решение.
При гидравлическом расчете трубопроводов с перепадом высот входа и выхода не забывайте добавлять (или отнимать) к результатам статическое давление. Для воды – перепад высот в 10 метров ≈ 1 кг/см2.
Уважаемые читатели, Ваши мысли, замечания и предложения всегда интересны коллегам и автору. Пишите их внизу, в комментариях к статье!
Прошу уважающих труд автора скачивать файл после подписки на анонсы статей!
Не забывайте подтвердить подписку кликом по ссылке в письме, которое придет к вам на указанную почту (может прийти в папку «Спам»)!!!
Ссылка на скачивание файла: gidravlicheskiy-raschet-truboprovodov (xls 57,5KB).
Важное и, думаю, интересное продолжение темы читайте здесь.
Другие статьи автора блога
На главную
Статьи с близкой тематикой
Отзывы
5.4. Гидравлический расчет сложных трубопроводов
Разветвленные
трубопроводы
Трубопровод,
имеющий общее сечение, в котором
разделяются или смыкаются несколько
ветвей труб, называется разветвленным.
Представленный
на схеме (рис. 5.7) разветвленный трубопровод
в сечении В-В
расходится на
три трубы. По каждой из труб осуществляется
подача воды в резервуары на геодезические
высоты
 ,
,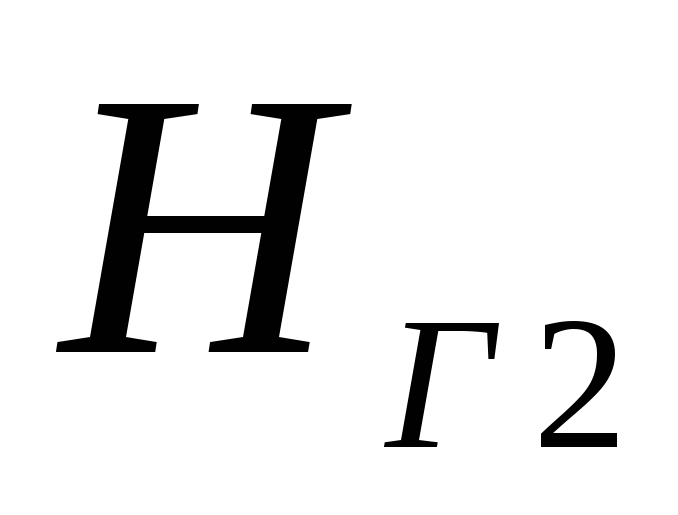 ,
,
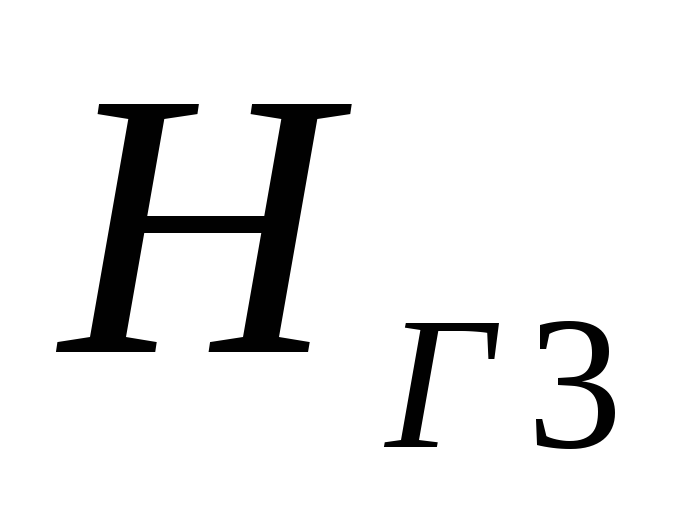 .
.
Трубы имеют
различные диаметры
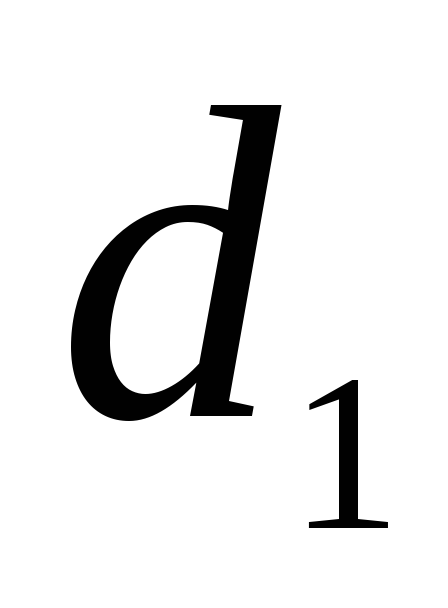 ,
,
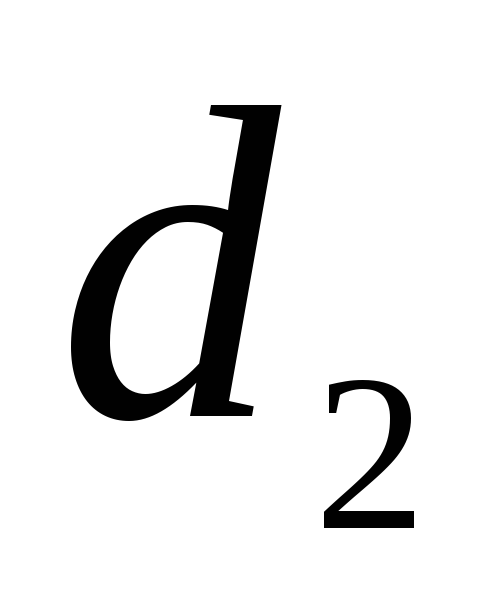 ,
,
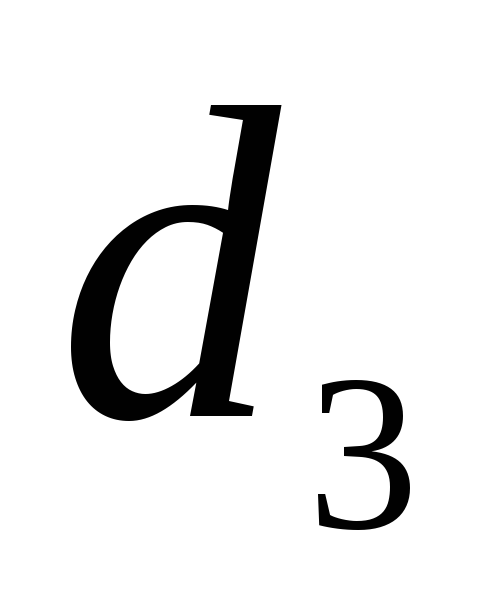
и длины
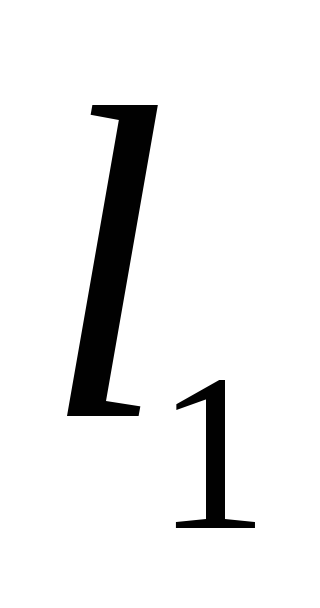 ,
,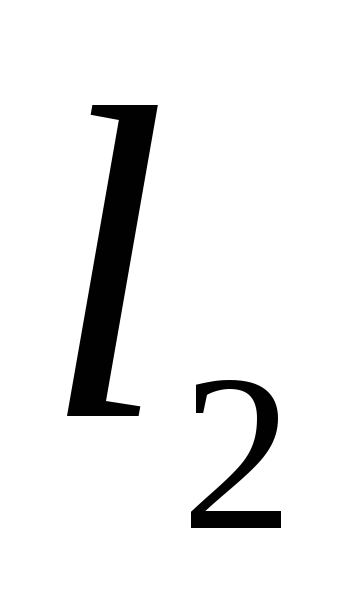 ,
,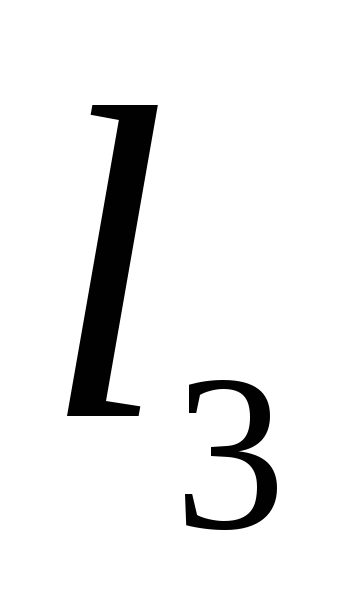 .
.
Общий расход в основном трубопроводе
до разветвления —Q.
В разветвленных
трубах расходы соответственно равны
 ,
, ,
,
 .
.
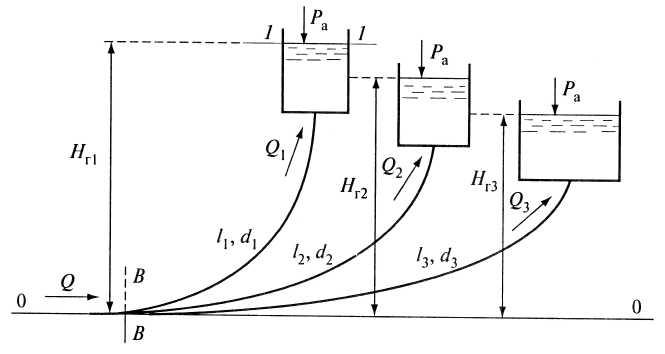
Рис.
5.7. Схема
разветвленного
трубопровода
Для разветвленного
трубопровода можно написать следующее
уравнение:
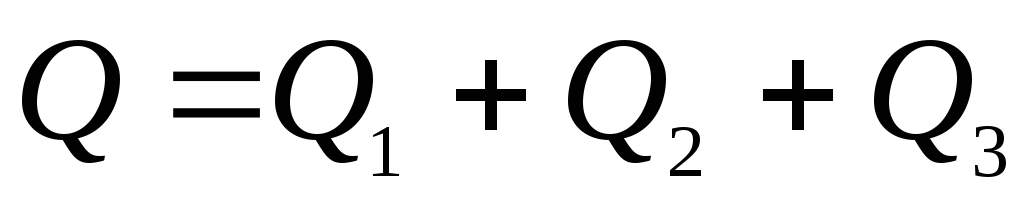 . (5.21)
. (5.21)
Запишем уравнение
Бернулли для сечения В-В
и, например,
для сечения первого трубопровода 1-1,
которое совпадает с уровнем воды в
резервуаре. Пусть плоскость сравнения
проходит через сечение В-В.
Давление на
свободной поверхности в резервуаре —
атмосферное, а давление в сечении В-В
принимаем
равным абсолютному, т.е.
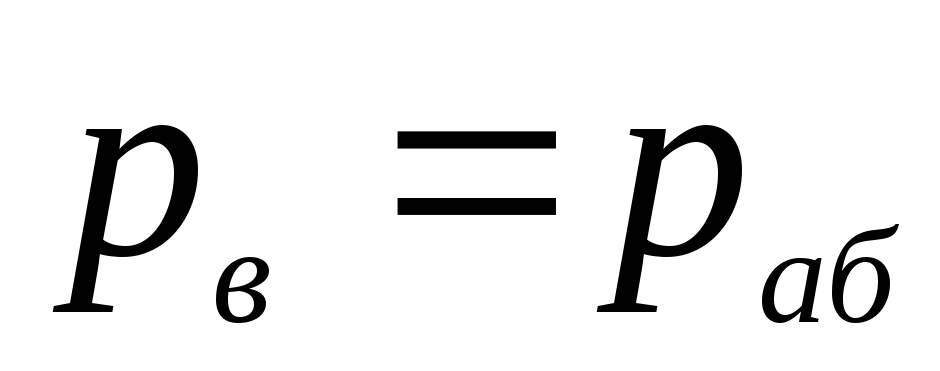 :
:
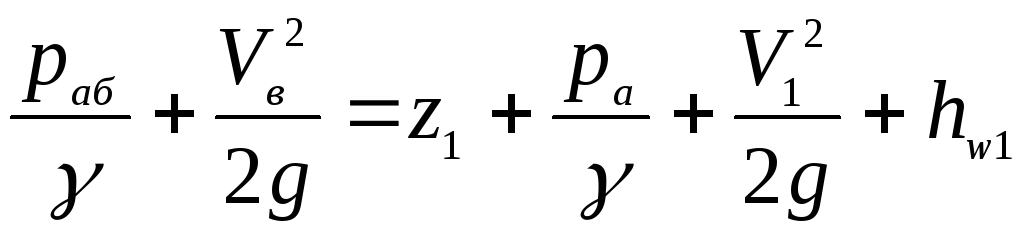 ,
,
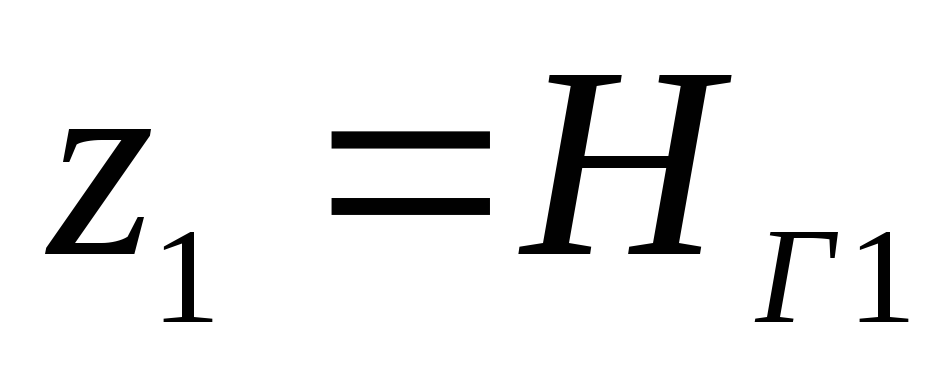 ;
;
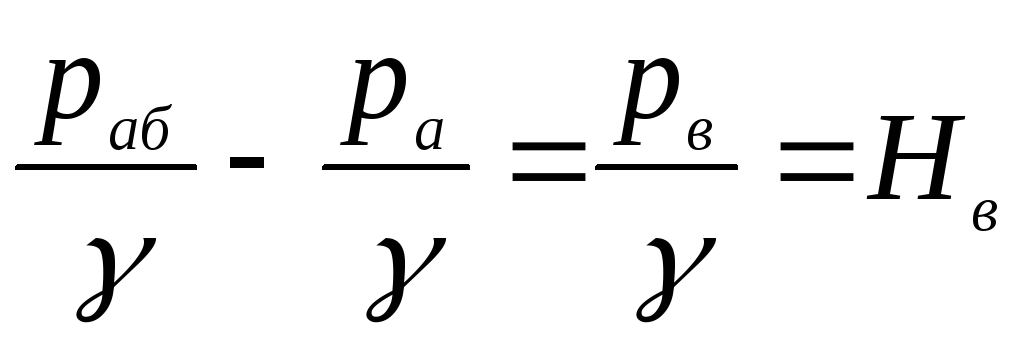 .
.
Скоростным напором
в сечении В-В
пренебрегаем:
 .
.
Скорость в сечении1-1
резервуара
считаем равной нулю, тогда
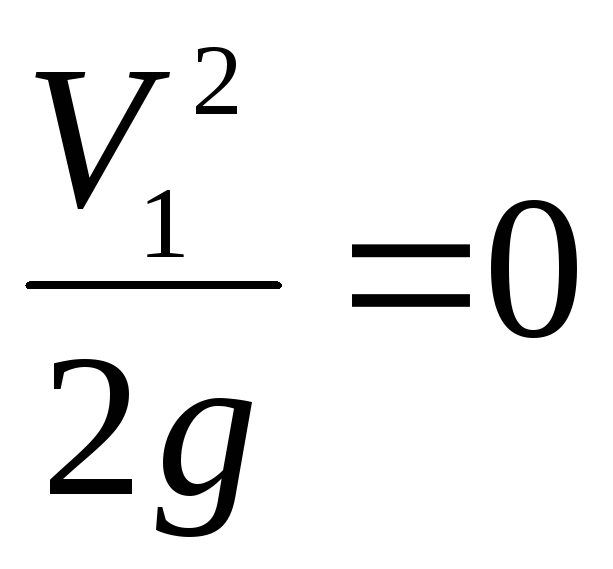 .
.
Напор
 в сеченииВ-В
в сеченииВ-В
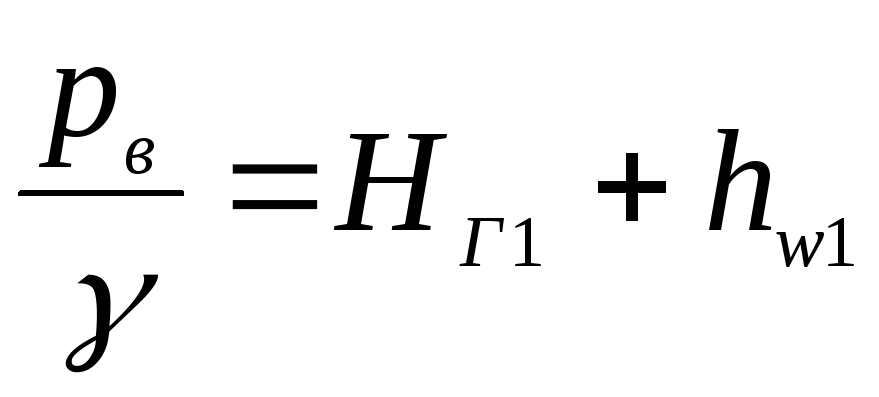 . (5.23)
. (5.23)
Будем считать
трубопровод длинным, тогда
 и, следовательно, потери в нем можно
и, следовательно, потери в нем можно
определить по водопроводной формуле
(4.44):
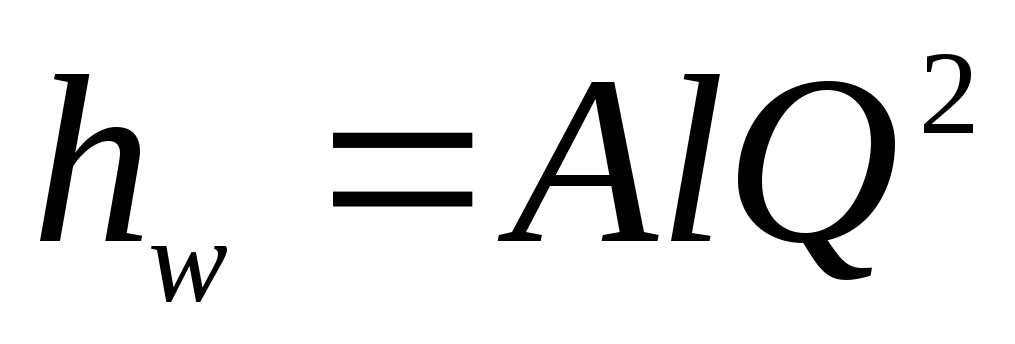 .
.
Напор в сечении
В-В
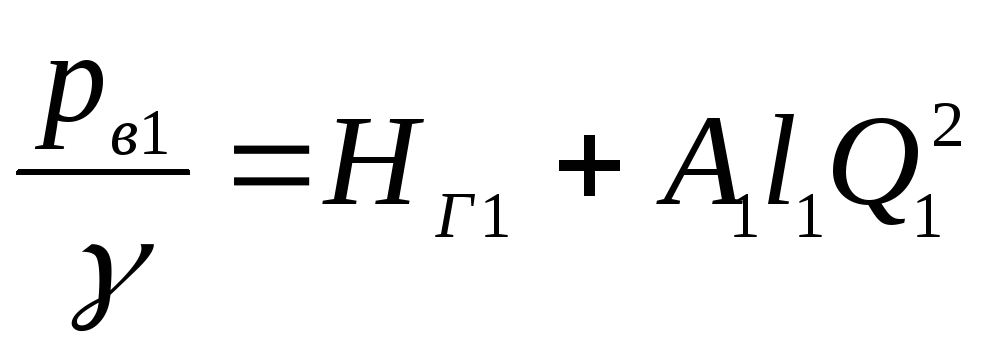 . (5.24)
. (5.24)
Аналогично,
рассматривая два других трубопровода,
можно получить:
 ; (5.25)
; (5.25)
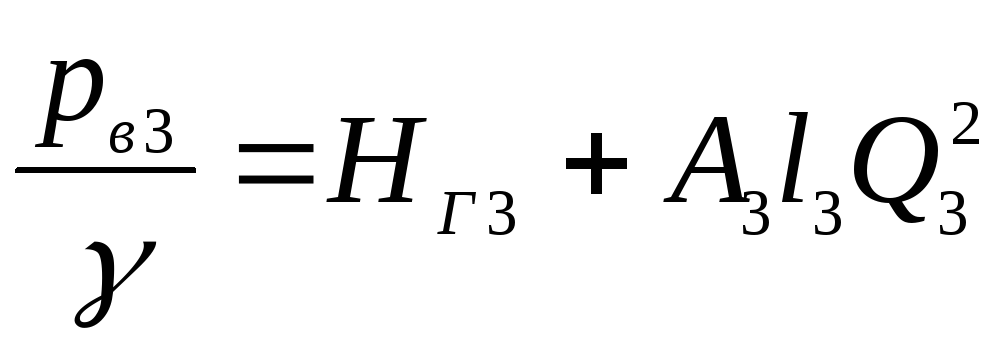
Таким образом, при
расчете простейшей схемы разветвленного
трубопровода используются полученные
уравнения (5.24) и (5.25), а также уравнение
(5.21). Совместное решение этих уравнений
позволяет определить все три расхода
—
 ,
, ,
,
 .
.
♦ Пример 5.5
Из водонапорной
башни в трубопровод (рис. 5.8), состоящий
из стальных труб, подается вода расходом
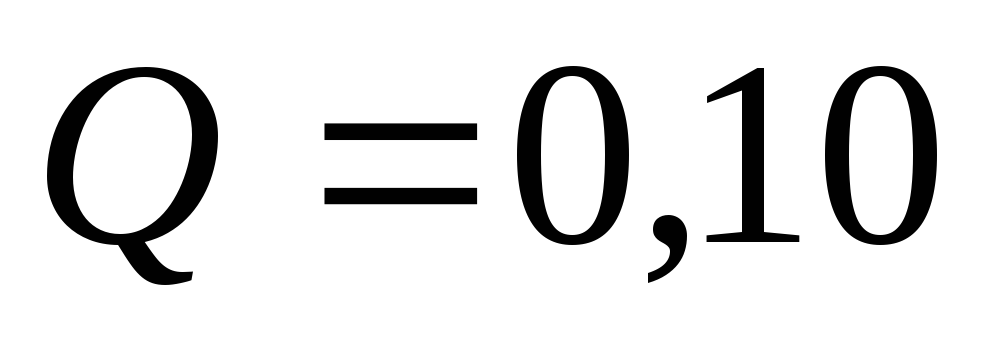 м3/с.
м3/с.
Длина трубы
до разветвления
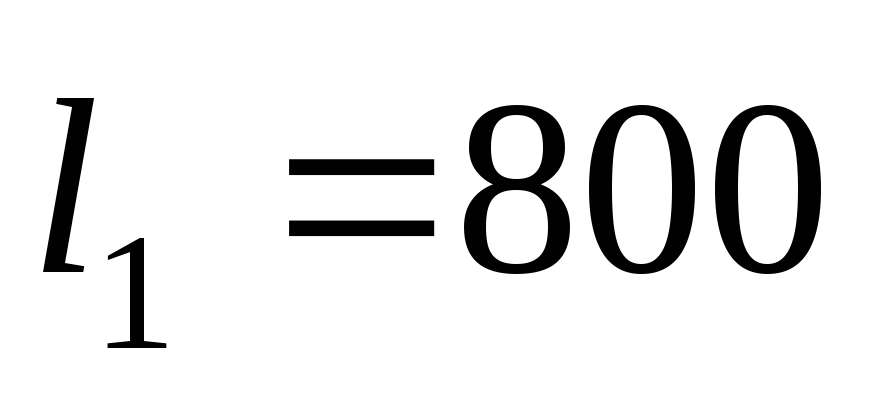 м, диаметр
м, диаметр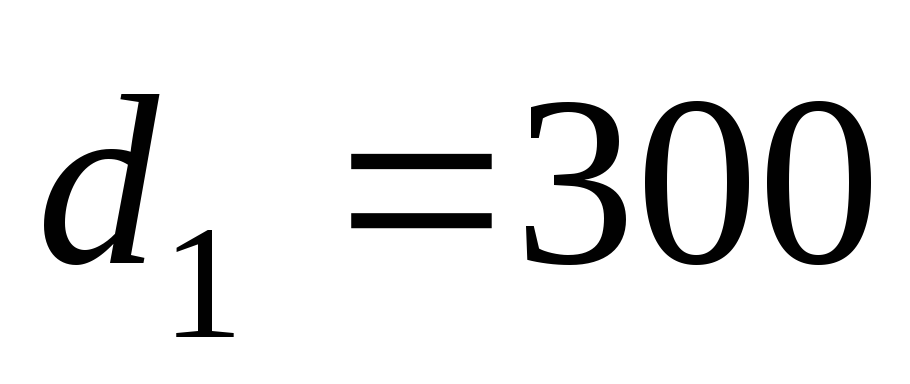 мм. В сеченииВ-В
мм. В сеченииВ-В
трубопровод
разветвляется на два трубопровода,
длины и диаметры которых соответственно
равны:
 м,
м,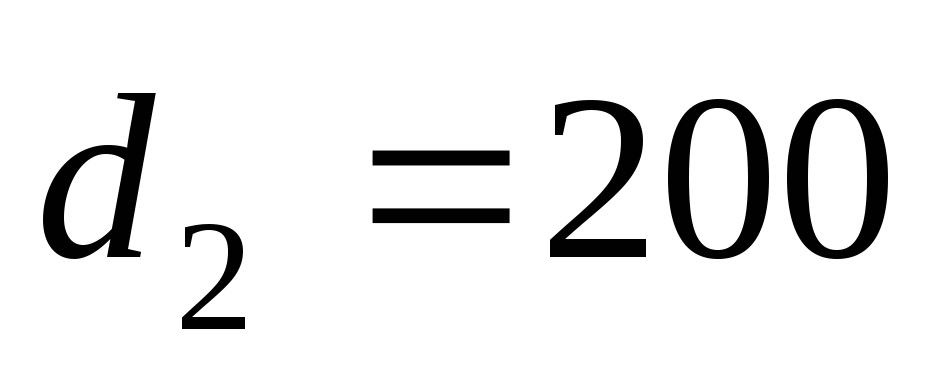 мм;
мм; м,
м,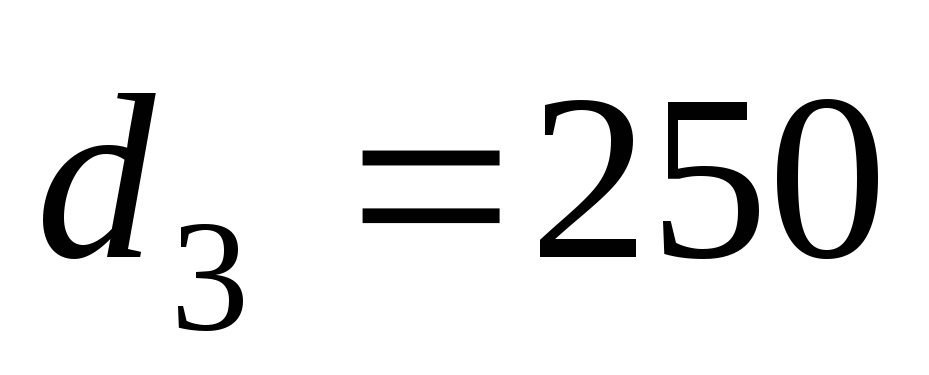 мм.
мм.
Определить расходы
в каждой ветви трубопровода. Геодезические
отметки подачи воды
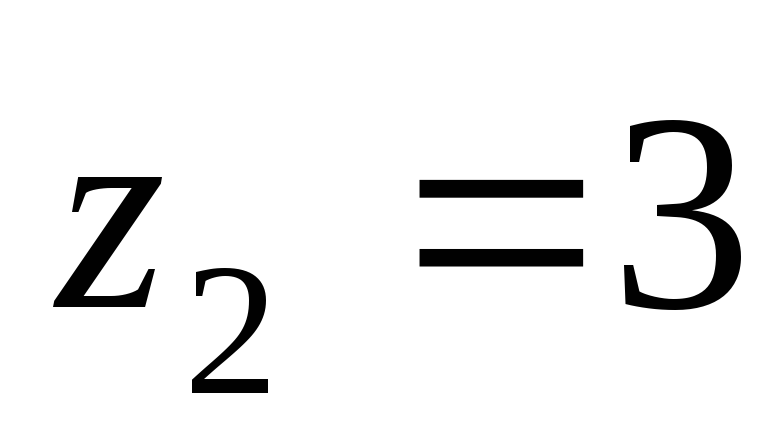 м и
м и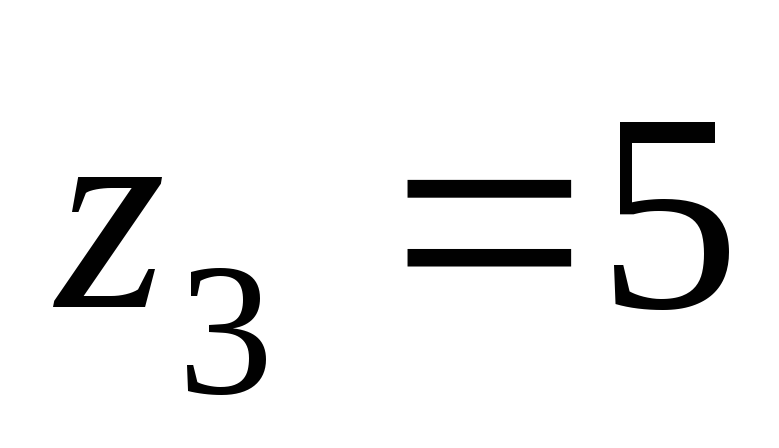 м.
м.
Расстояние от уровня воды в башне до
плоскости 0-0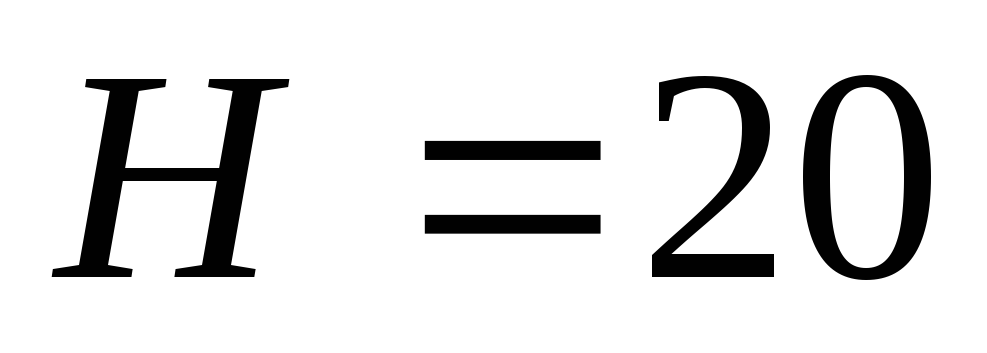 м. Местными сопротивлениями пренебречь.
м. Местными сопротивлениями пренебречь.
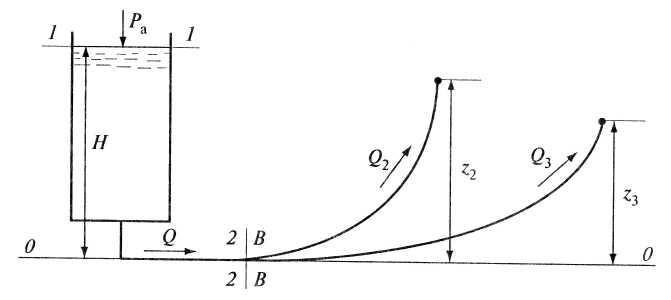
Рис.
5.8. К
примеру
5.5
Напор в сечении
В-В
определим,
используя уравнение Бернулли, приняв
плоскость сравнения 0-0. Первое сечение
совпадает со свободной поверхностью
воды водонапорной башни, второе сечение
— сечение В-В.
Принимаем
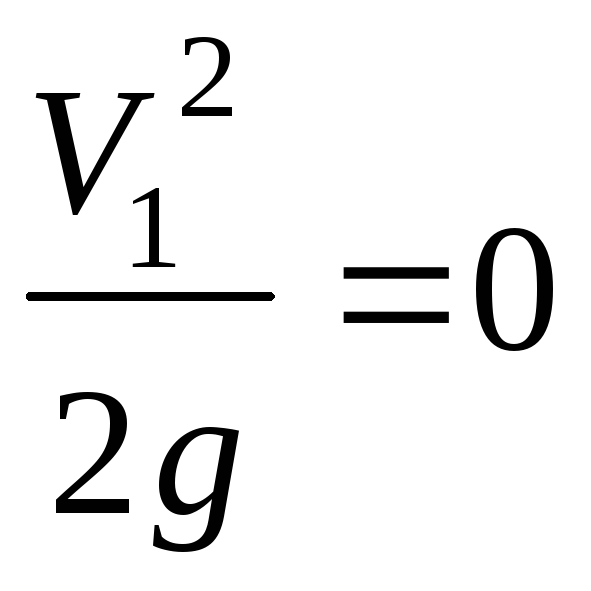 ,
,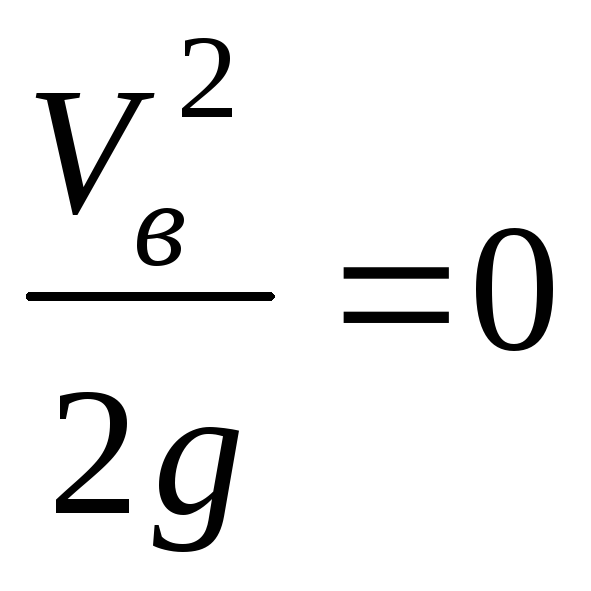 ,
,
согласно условию примера местные потери
равны нулю. Тогда из уравнения Бернулли
получим
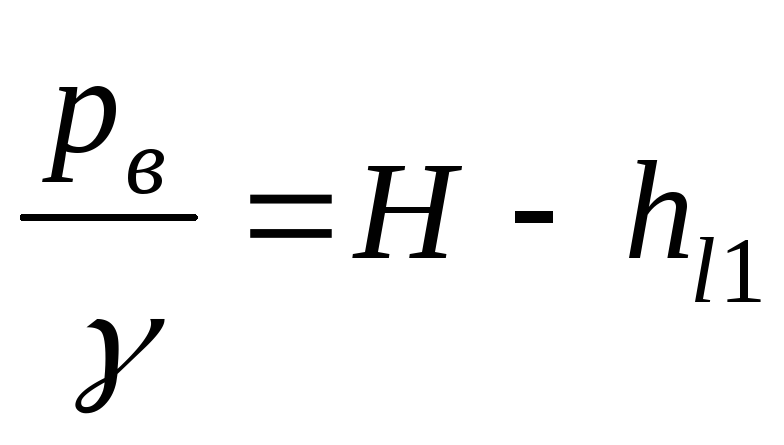 ,
,
где
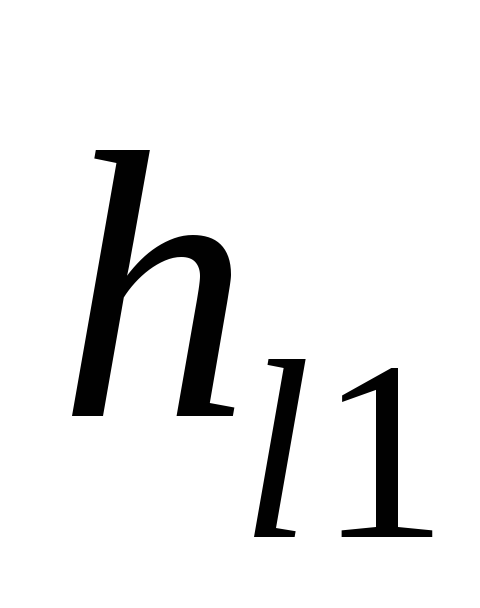
— гидравлические
потери по длине трубопровода до
разветвления.
По табл. 5.3 для
стальной трубы диаметром
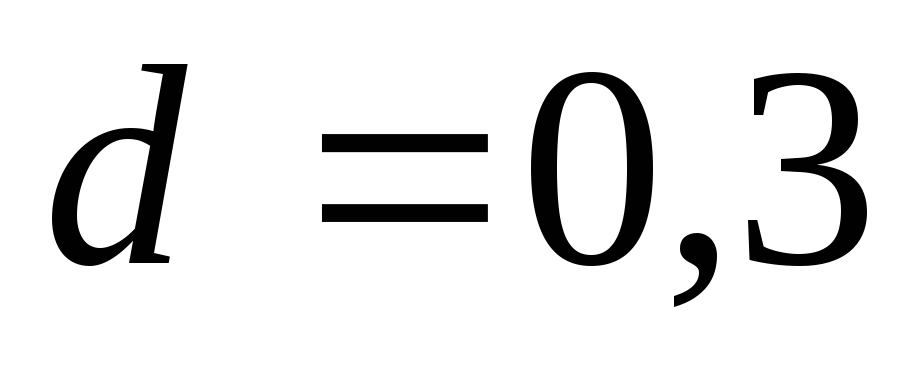 м находим удельное сопротивление
м находим удельное сопротивление с2/м6.
с2/м6.
Потери напора по длине
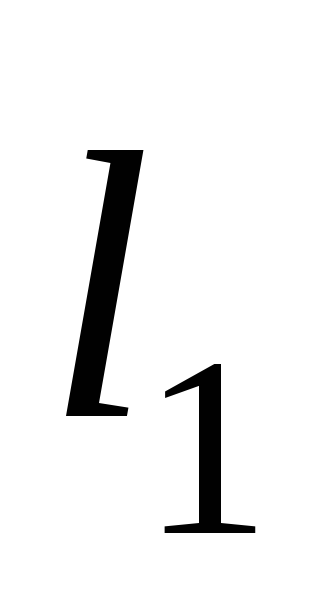 в трубопроводе при расходеQ
в трубопроводе при расходеQ
 м.
м.
Напор в сечении
В-В
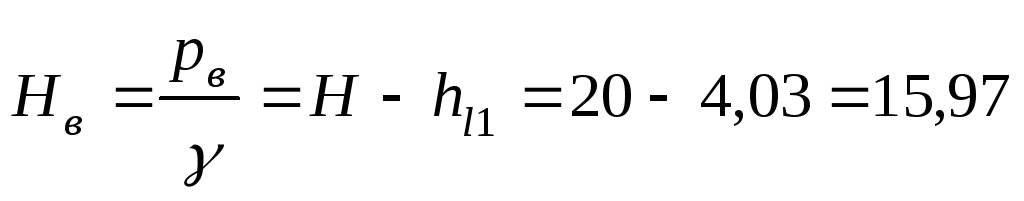 м.
м.
Согласно формуле
(5.25) напор в сечении
 .
.
По табл. 5.3 для
трубы
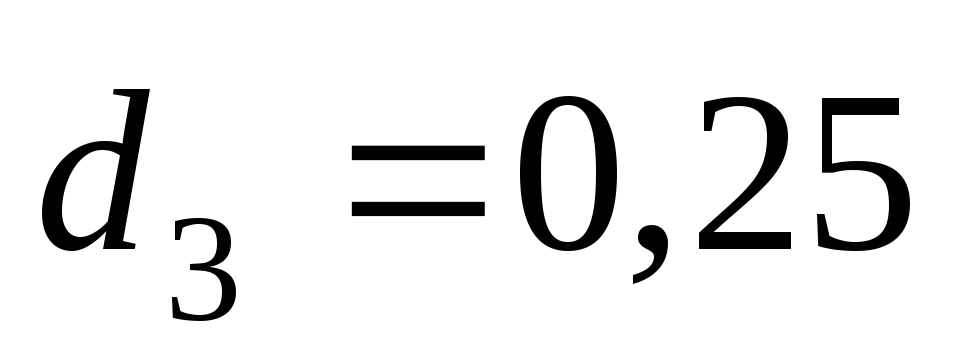 м находим
м находим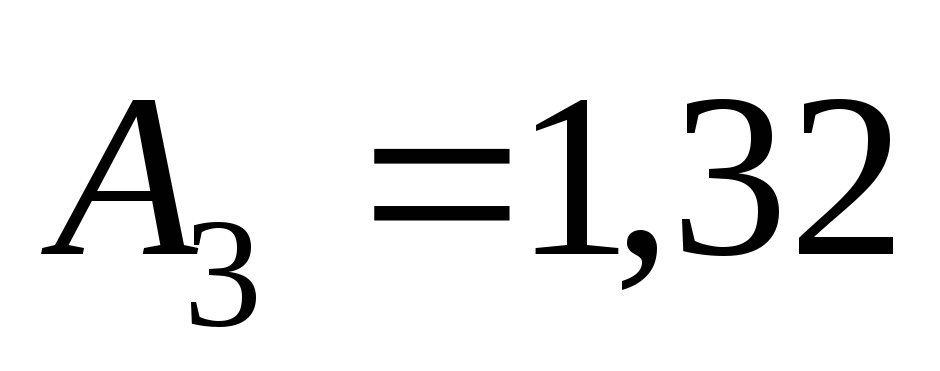 с2/м6;
с2/м6;
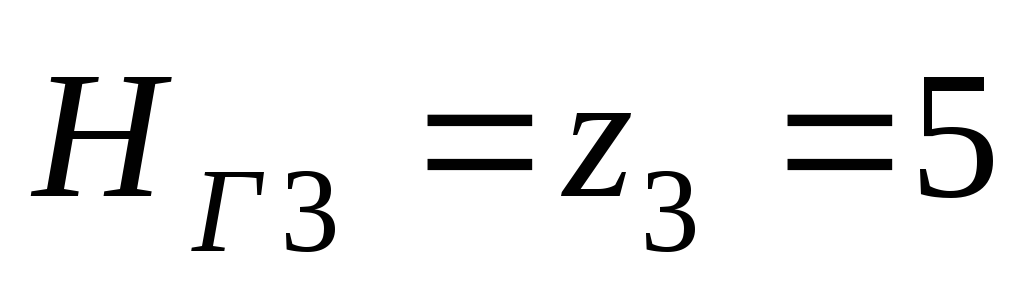 м.
м.
Расход в этом
трубопроводе
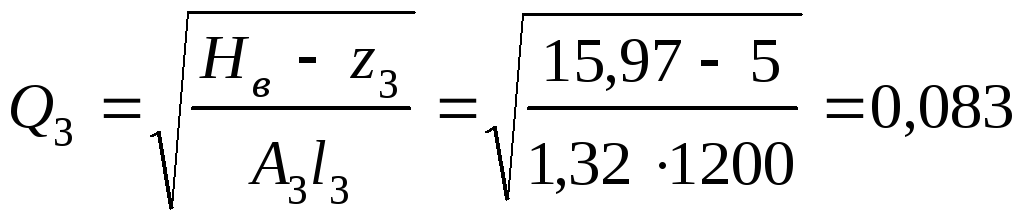 м3/с.
м3/с.
Расход в трубопроводе
диаметром
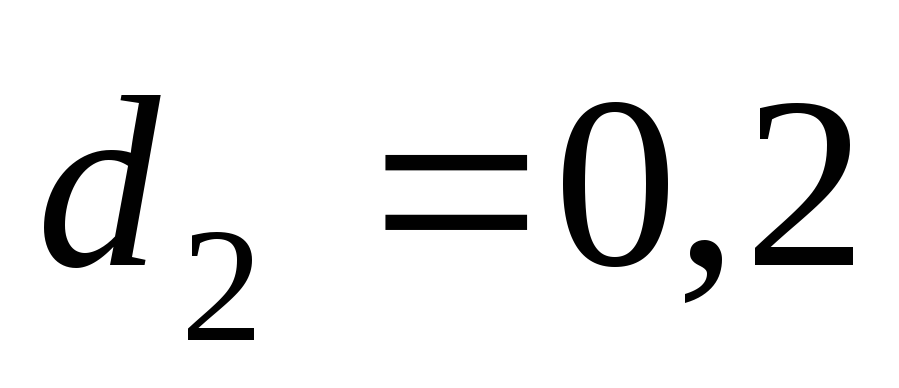 м
м
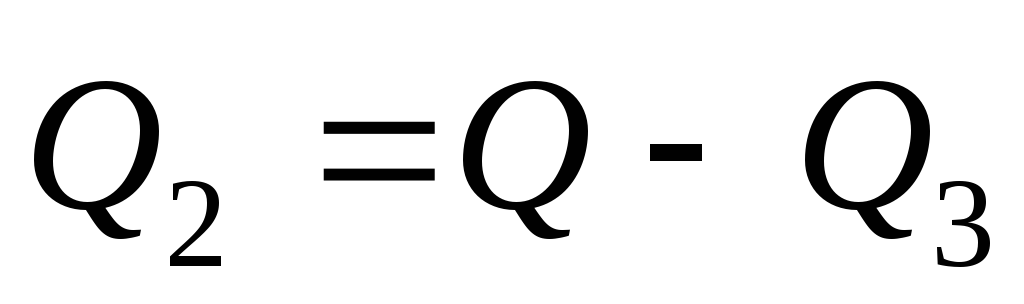 ;
;
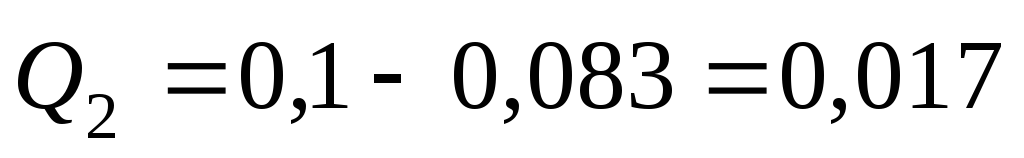 м3/с
м3/с
Параллельные
трубопроводы
Параллельными
трубопроводами
называются трубопроводы, которые имеют
свое начало в общем сечении и заканчиваются
в другом общем сечении.
На рис. 5.9 представлена
схема параллельного соединения трех
трубопроводов, имеющих разную длину и
диаметр.

Рис.
5.9. Схема
параллельного
соединения
трех трубопроводов
В точке В
напор
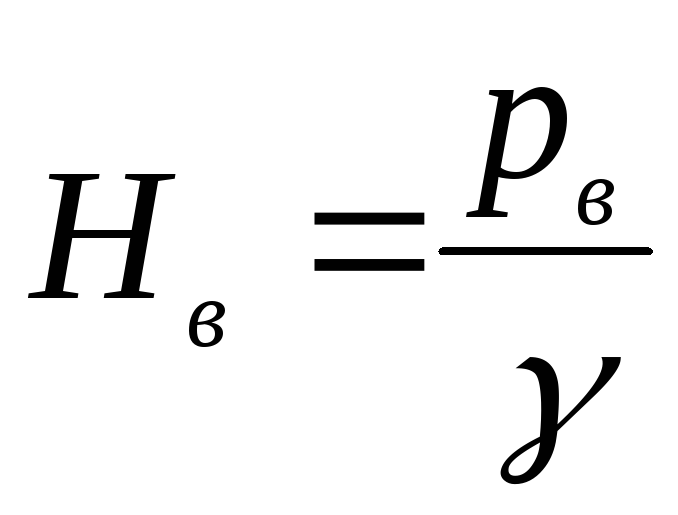 ,
,
а в точкеС
напор
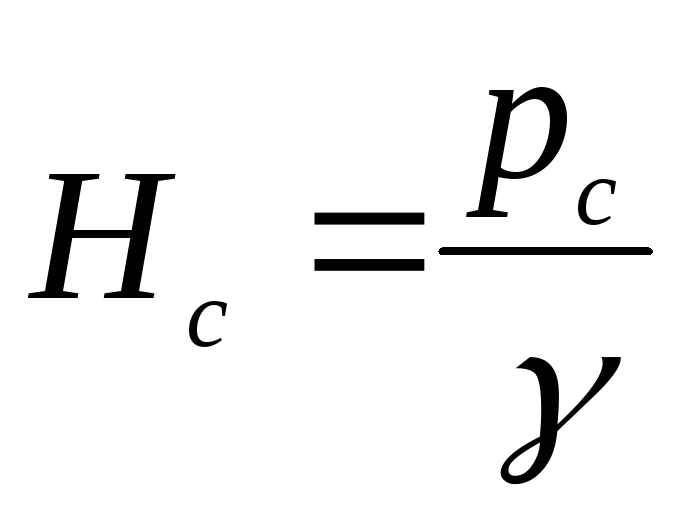 .
.
Расход до разветвления
(точка В)
равен сумме
расходов в трубах 1, 2 и 3:
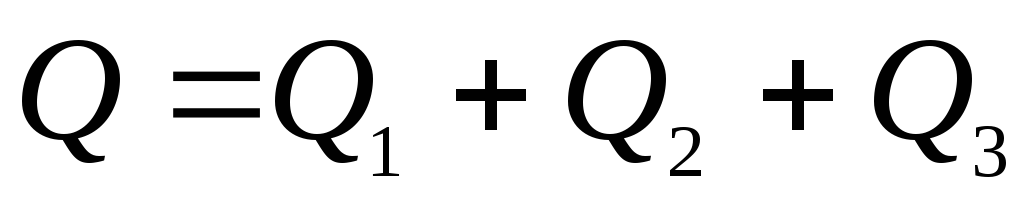 .
.
Разность
напоров в точках
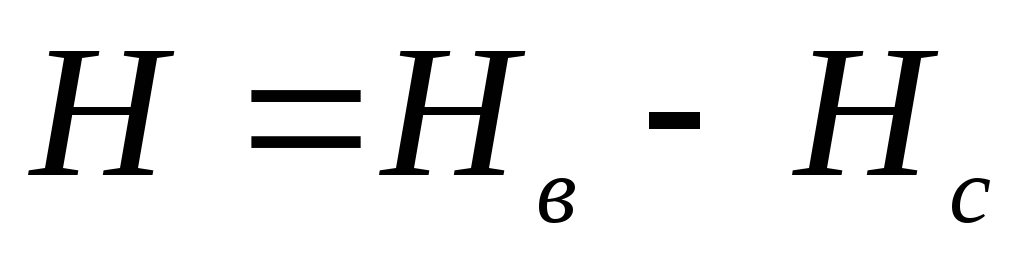 .
.
ТочкиВ
и С
принадлежат
всем трем трубопроводам. Разность
напоров в местах соединения труб
одинакова, следовательно, гидравлические
потери в каждой ветви трубопровода:
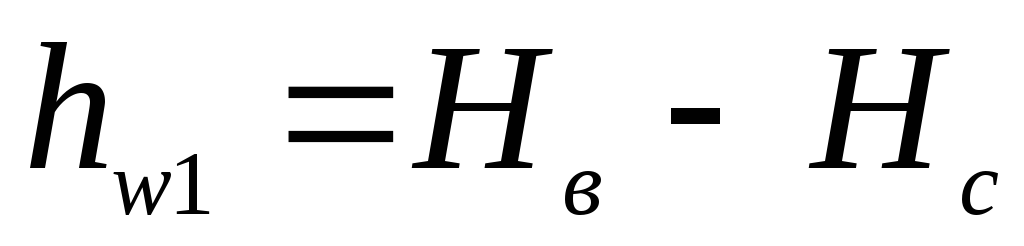 ;
;
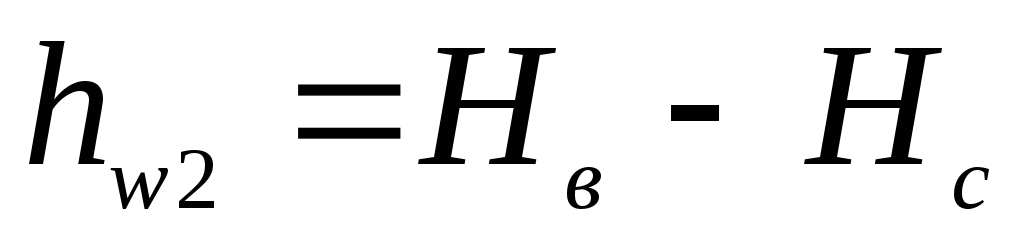 ; (5.26)
; (5.26)
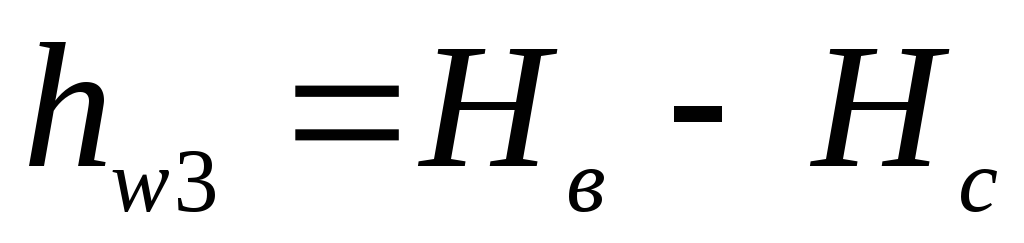 .
.
Таким образом,
можно считать, что гидравлические потери
во всех параллельно соединенных
трубопроводах независимо от их количества,
длины и диаметра одинаковые: .
Полагая, что
местные гидравлические потери малы по
сравнению с потерями по длине и используя
водопроводную формулу (4.44), получим
систему уравнений:
 ;
;
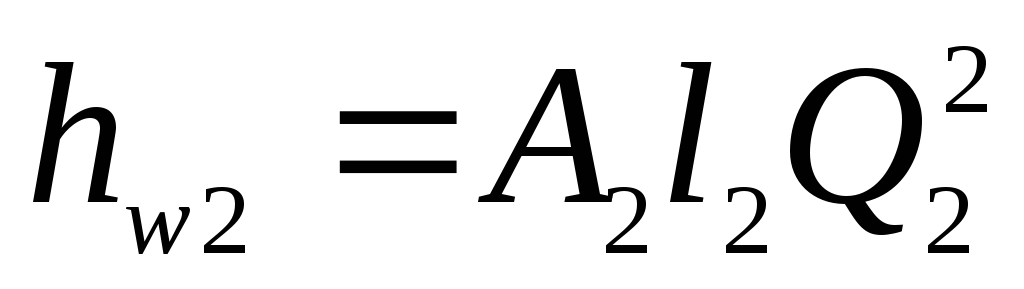 ; (5.27)
; (5.27)
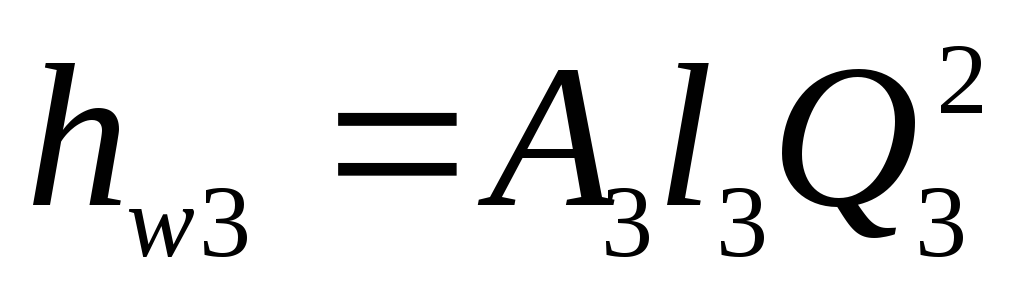 .
.

Рис.
5.10. Графики
характеристик
отдельных
параллельно
соединенных
трубопроводов
Расчет параллельно
соединенных трубопроводов заключается
в определении расходов в каждом из них
и основывается на использовании уравнений
(5.26) и (5.27). Количество уравнений
определяется числом трубопроводов,
присоединенных к сечениям В
и С.
Используя эти
уравнения, можно построить графики
функций характеристик отдельных
трубопроводов
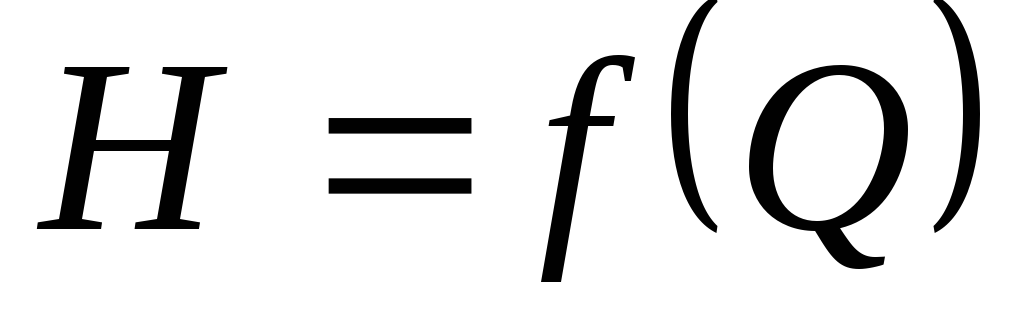
(рис. 5.10).
Для удобства
построения графиков можно применить
параметр
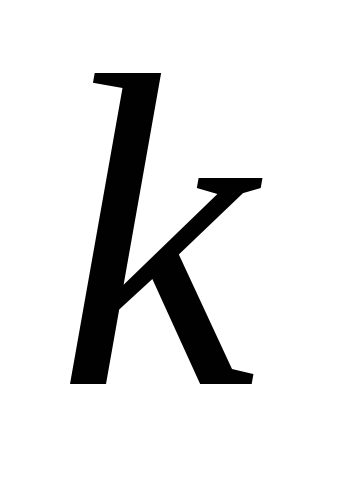
(сопротивление
трубопровода):
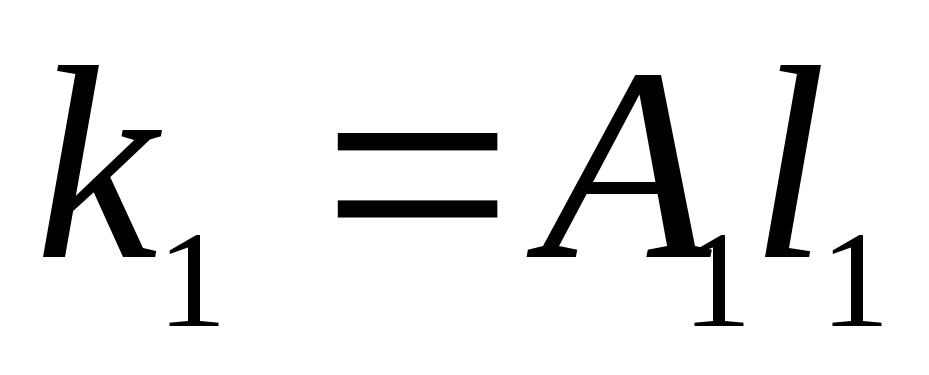 ;
;
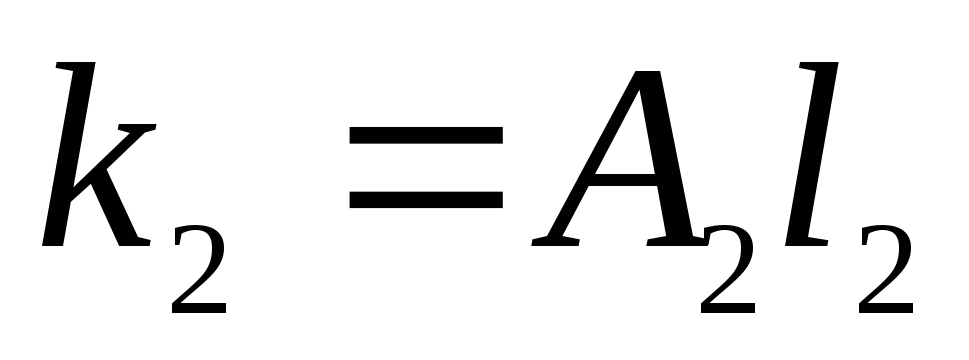 ;
;
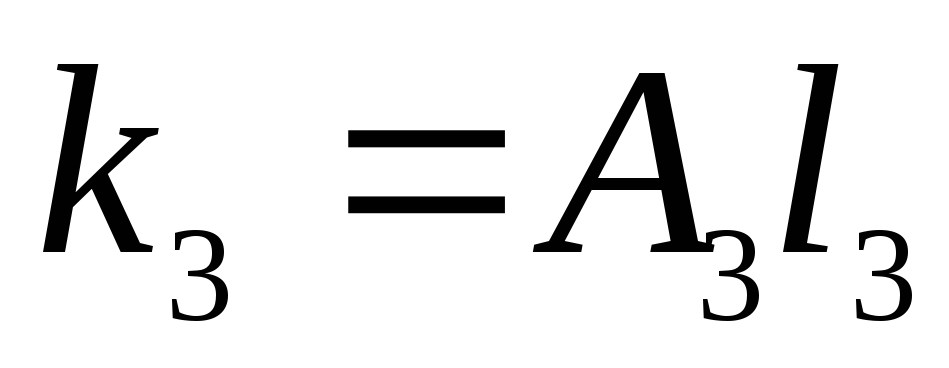 и т.д.
и т.д.
Зависимость
гидравлических потерь имеет следующий
вид:
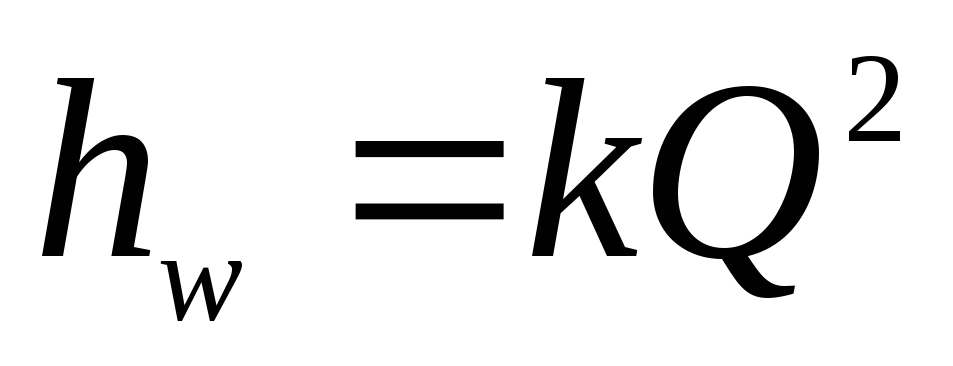 .
.
Характеристика
параллельно соединенного трубопровода
строится путем сложения по горизонтали
расходов
 при одинаковых
при одинаковых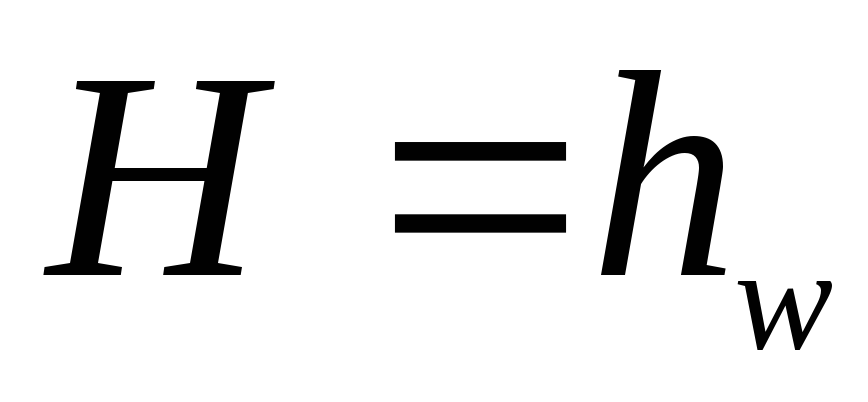 .
.
♦ Пример 5.6
На водоводе между
точками В
и С
установлены три параллельных трубопровода
(см. рис. 5.9). Расход в водоводе до
разветвления
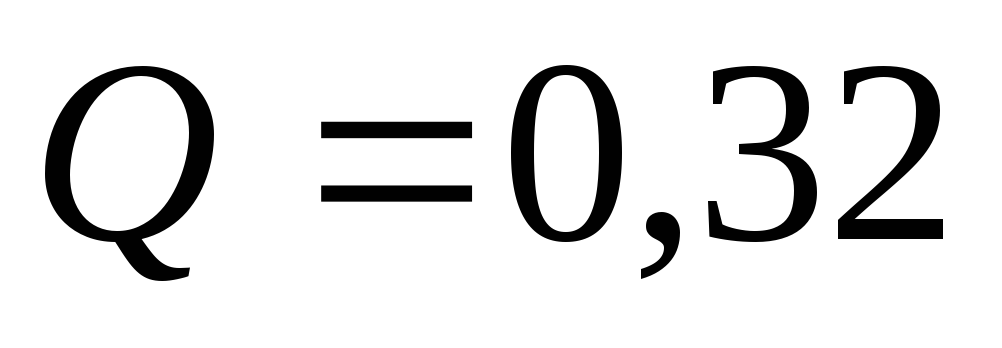 м3/с
м3/с
Длины и диаметры трубопроводов:
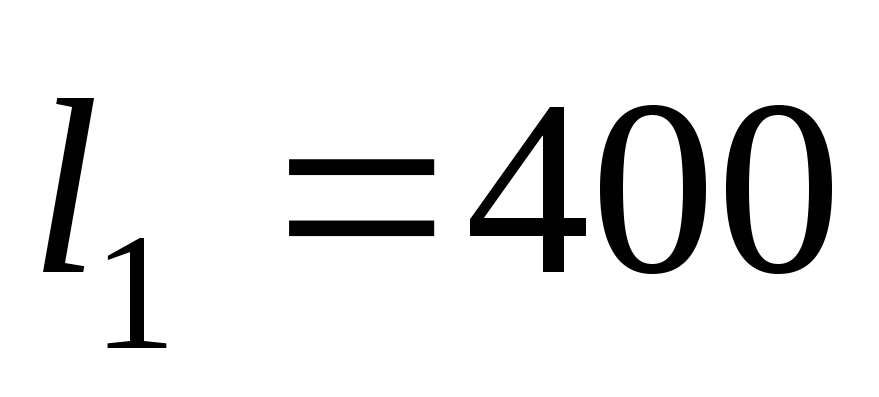 м,
м, м,
м,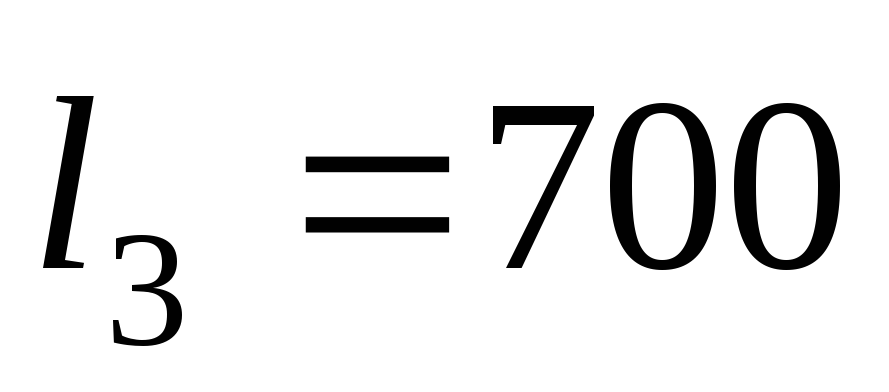 м;
м;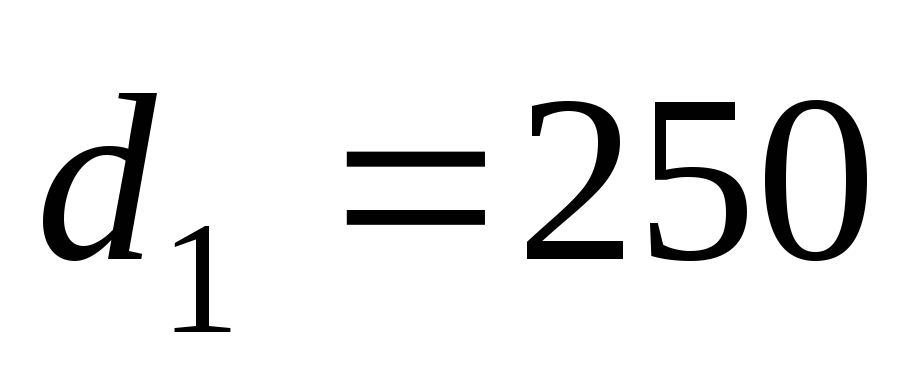 мм,
мм,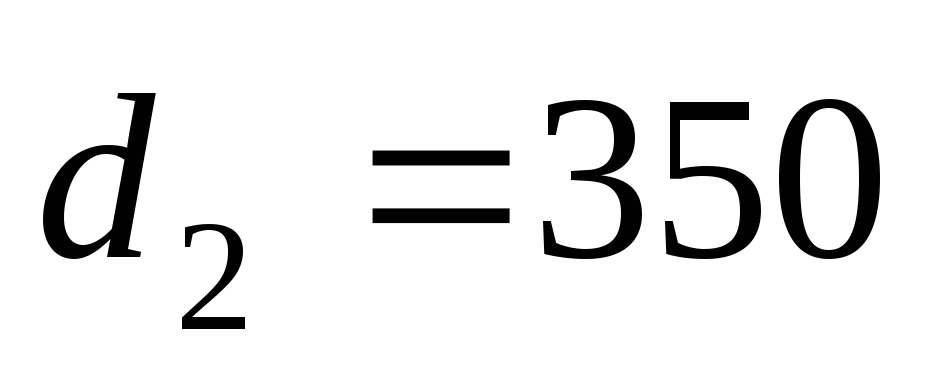 мм,
мм,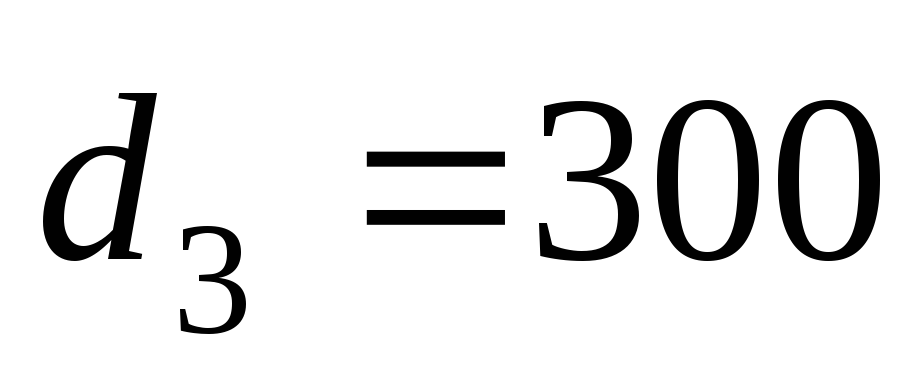 мм. Определить расходы в отдельных
мм. Определить расходы в отдельных
стальных трубопроводах и потери напора
между точкамиВ
и С.
Гидравлические
потери в трубопроводах 1, 2 и 3
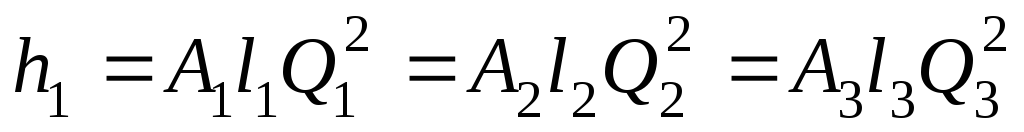 .
.
По табл. 5.3 находим
значения удельных сопротивлений для
стальных труб:
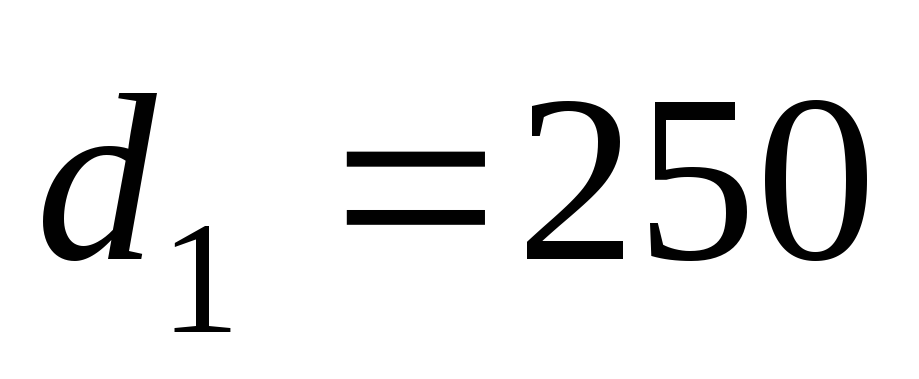 мм,
мм, 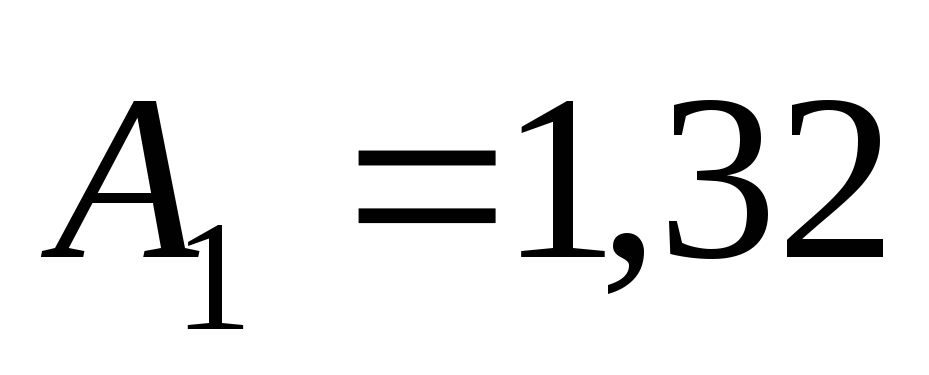 с2/м6;
с2/м6;
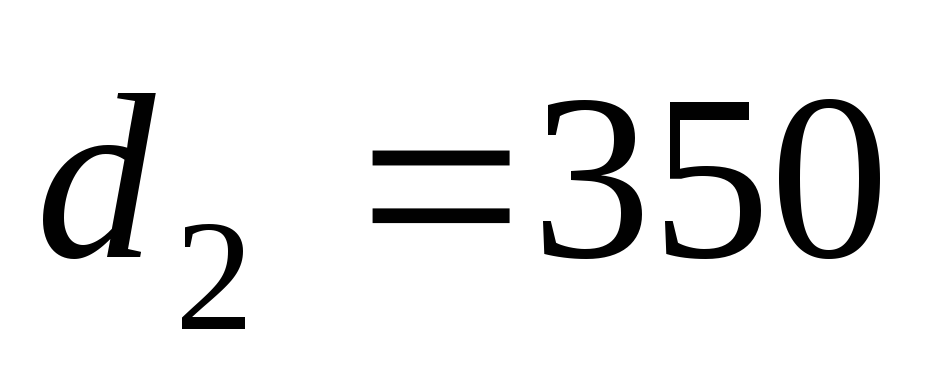 мм,
мм, 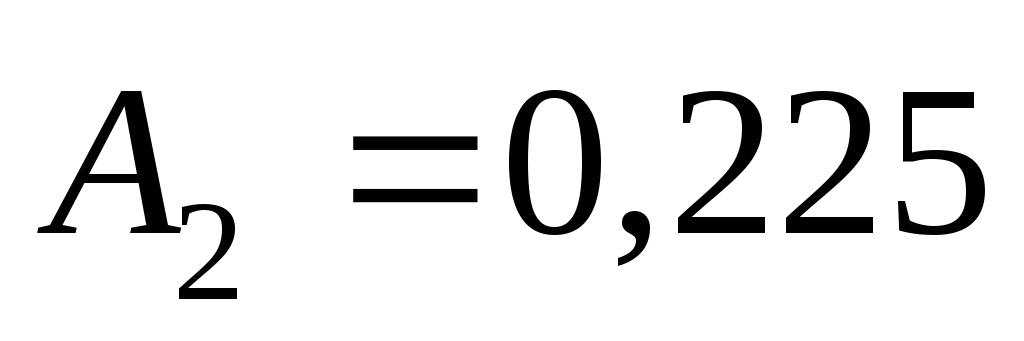 с2/м6;
с2/м6;
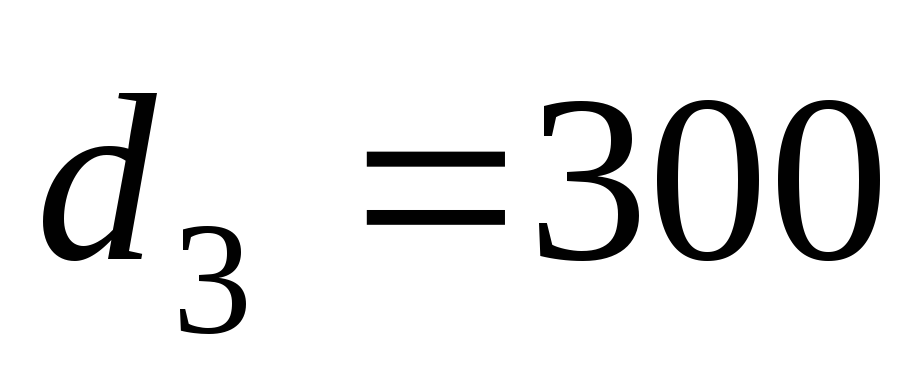 мм,
мм, 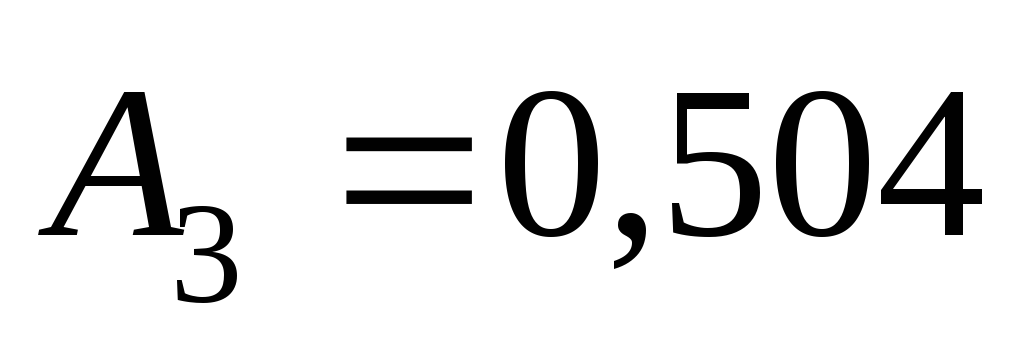 с2/м6.
с2/м6.
Выразим
 и
и через
через ,
,
используя
равенство потерь напора в трубопроводах,
получим:
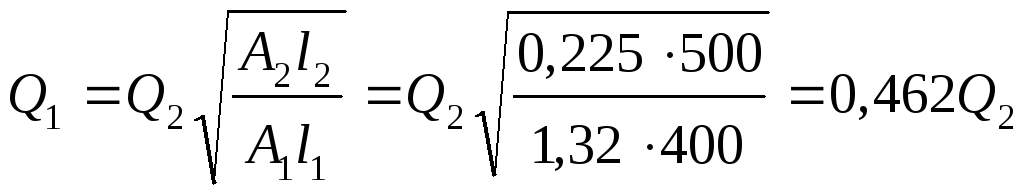 ;
;
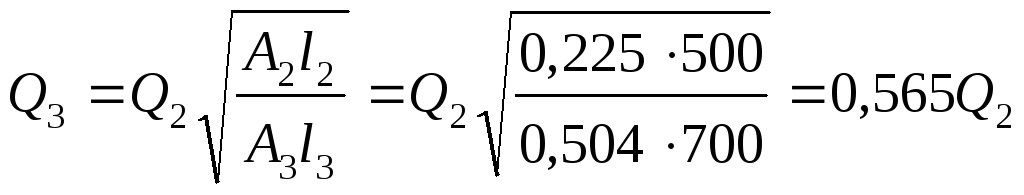 .
.
Расход в водоводе
равен сумме расходов в трубопроводах:
 .
.
Расход во втором
трубопроводе
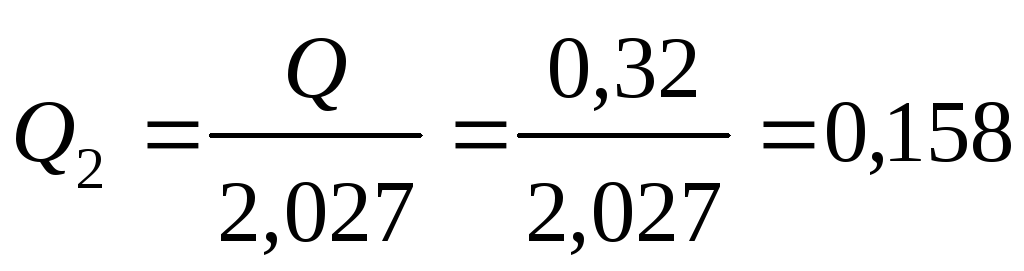 м3/с.
м3/с.
В первом трубопроводе
 м3/c.
м3/c.
В третьем трубопроводе
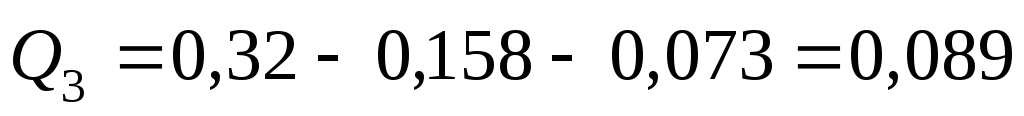 м3/с
м3/с
Потери напора
между точками В
и С
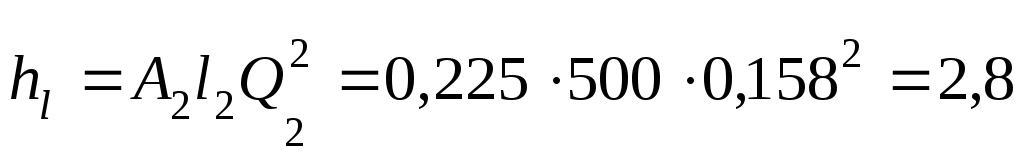 м.
м.
Гидравлический расчет сложных трубопроводов — Студопедия
К сложным трубопроводам относятся трубопроводы с переменным диаметром или расходом. Сложные трубопроводы: последовательно соединенные; параллельно соединенные; разветвленные. При гидравлическом расчете сложных трубопроводов решаются те же 3 задачи, что и при расчете простых трубопроводов. Особенность заключается в расчете потерь напора на трение.
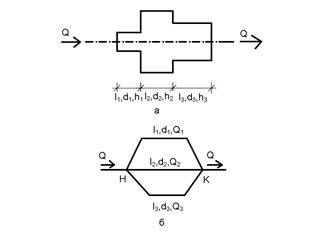
Рисунок 7.4 – Сложные трубопроводы
Последовательно соединенным называется трубопровод, состоящий из труб разного диаметра соединенных в одну нитку (рис.7.4,а).
Трубопровод разбивают на участки с одинаковым диаметром, на каждом из которых определяют потери; а общую сумму потерь между начальным и конечным сечением определяют как сумму потерь
hн-к=h1 +h2+h3.
Расход является постоянным
Q = const.
Параллельно соединенный трубопровод – трубопровод, имеющий две общие точки (рис.7.4,б). Такое соединение повышает надежность работы сети.
Расход находится сложением расходов на каждой ветке
Q=Q1+Q2+ Q3.
Потери между двумя точками являются величиной постоянной
hн-к=const.
Графоаналитический метод расчета трубопроводов основан на построении характеристик трубопровода и кривых потребного напора.
Характеристикой трубопровода называется зависимость потерь напора от расхода.
В общем случае, задавая различные значения расхода и подставляя в формулу потерь напора, получаем значения потерь напора и строим график (рис.7.5).
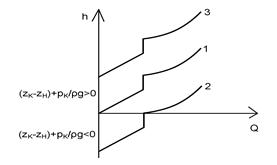
Рисунок 7.5 – Характеристика простого трубопровода
Потребным напором называется напор в начале сечения трубопровода, необходимый для перемещения жидкости от начального до конечного сечения
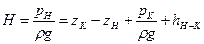 ,
,
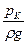 – остаточный свободный напор;
– остаточный свободный напор;
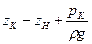 – приведенный геометрический напор.
– приведенный геометрический напор.
Приведенный геометрический напор может быть как положительной, так и отрицательной величиной. Поэтому график потребного напора располагается равноудалено от характеристики трубопровода. График потерь напора и характеристик трубопровода строится только для простого трубопровода. Для сложного трубопровода находится построением.
При последовательном соединении (рис.7.6.а)
Q = const;
h = h1 + h2
При параллельном соединении (рис.7.6,б)
h = const;
Q = Q1 + Q2.
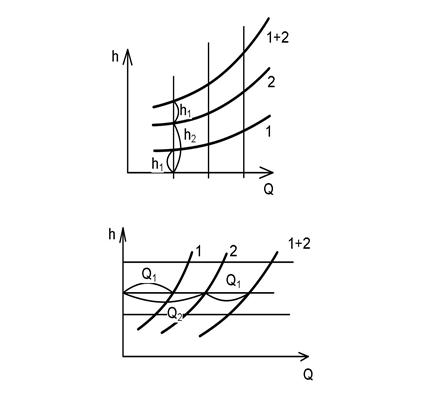
Рисунок 7.6 Графики совместной работы сложных трубопроводов
5.4. Гидравлический расчет сложных трубопроводов
Разветвленные
трубопроводы
Трубопровод,
имеющий общее сечение, в котором
разделяются или смыкаются несколько
ветвей труб, называется разветвленным.
Представленный
на схеме (рис. 5.7) разветвленный трубопровод
в сечении В-В
расходится на
три трубы. По каждой из труб осуществляется
подача воды в резервуары на геодезические
высоты
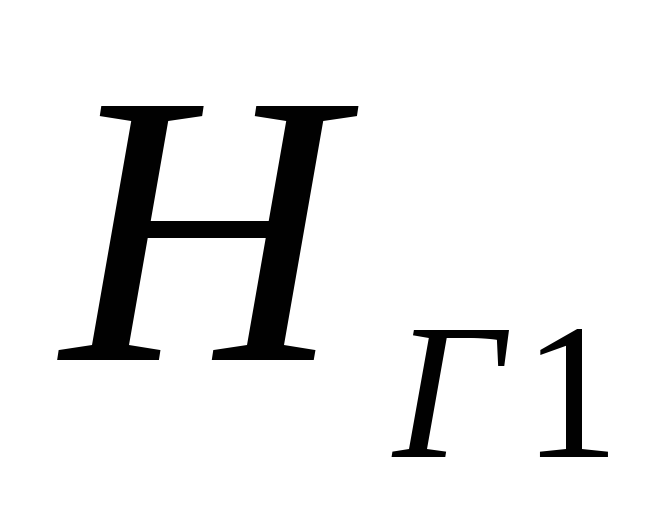 ,
,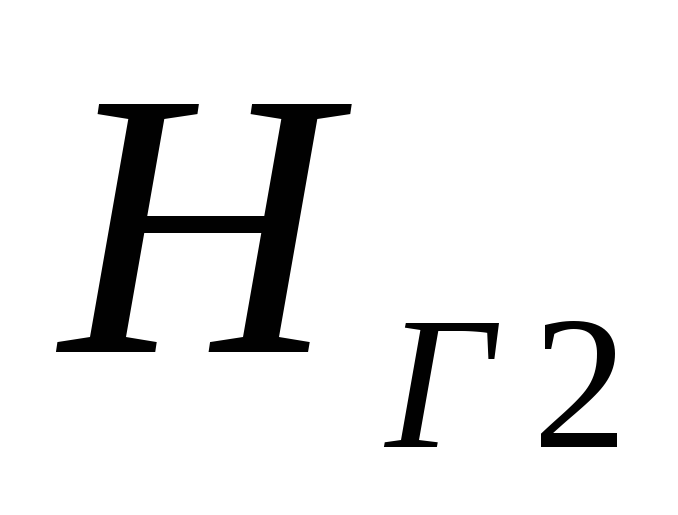 ,
,
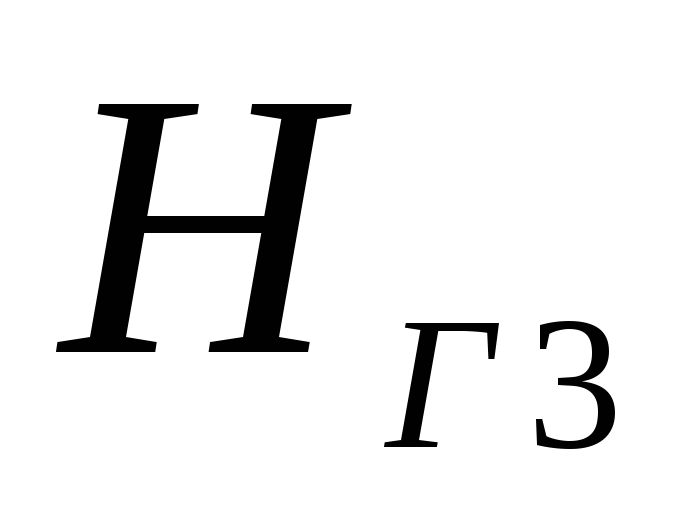 .
.
Трубы имеют
различные диаметры
 ,
,
 ,
,
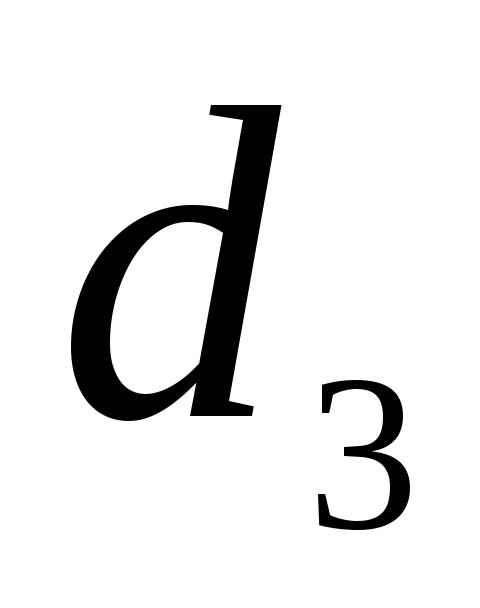
и длины
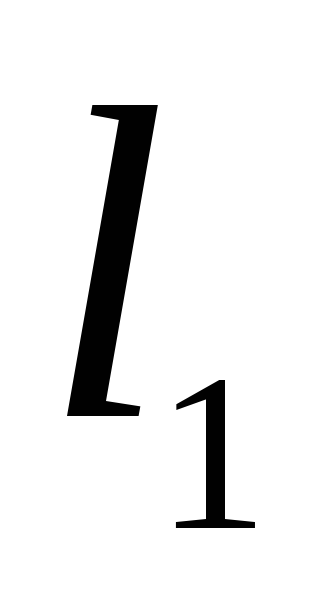 ,
,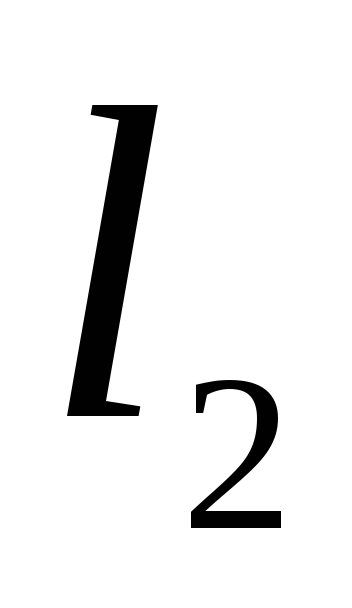 ,
,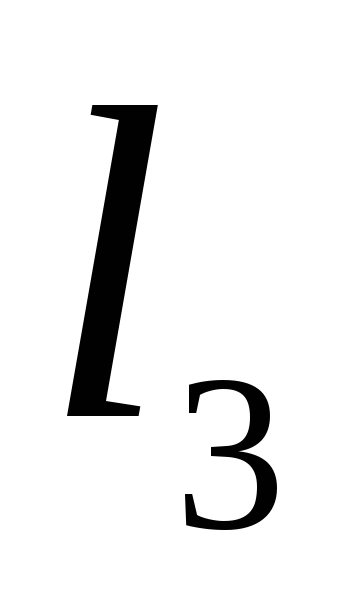 .
.
Общий расход в основном трубопроводе
до разветвления —Q.
В разветвленных
трубах расходы соответственно равны
 ,
, ,
,
 .
.
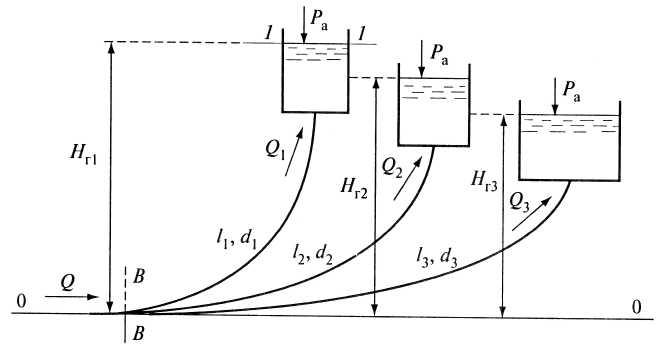
Рис.
5.7. Схема
разветвленного
трубопровода
Для разветвленного
трубопровода можно написать следующее
уравнение:
 . (5.21)
. (5.21)
Запишем уравнение
Бернулли для сечения В-В
и, например,
для сечения первого трубопровода 1-1,
которое совпадает с уровнем воды в
резервуаре. Пусть плоскость сравнения
проходит через сечение В-В.
Давление на
свободной поверхности в резервуаре —
атмосферное, а давление в сечении В-В
принимаем
равным абсолютному, т.е.
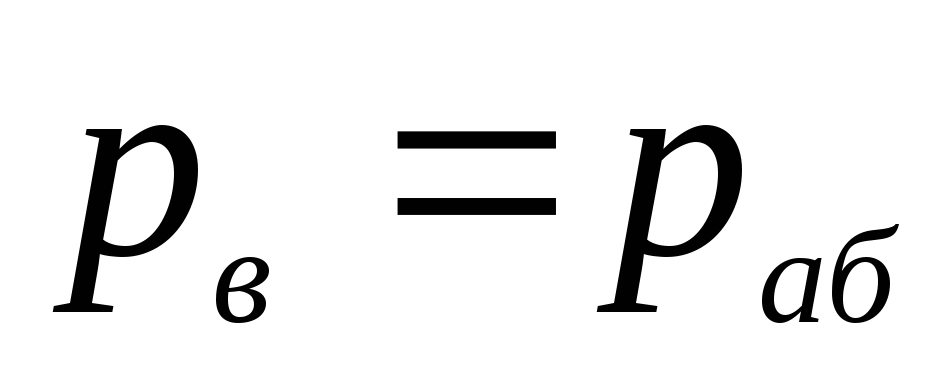 :
:
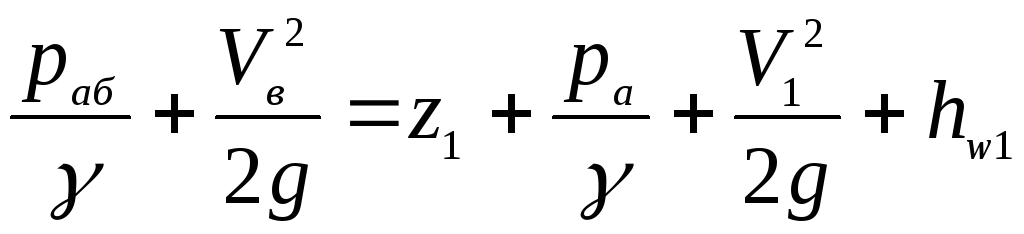 ,
,
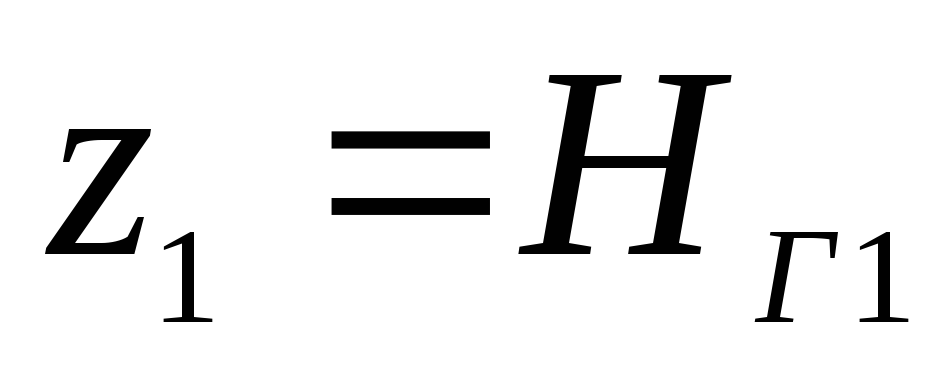 ;
;
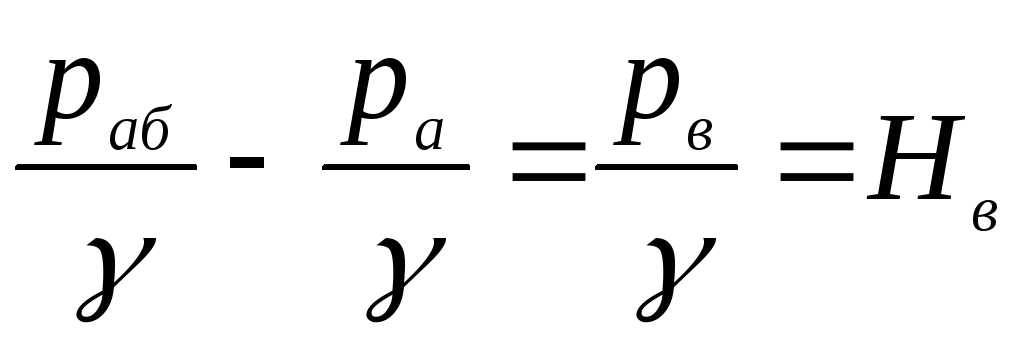 .
.
Скоростным напором
в сечении В-В
пренебрегаем:
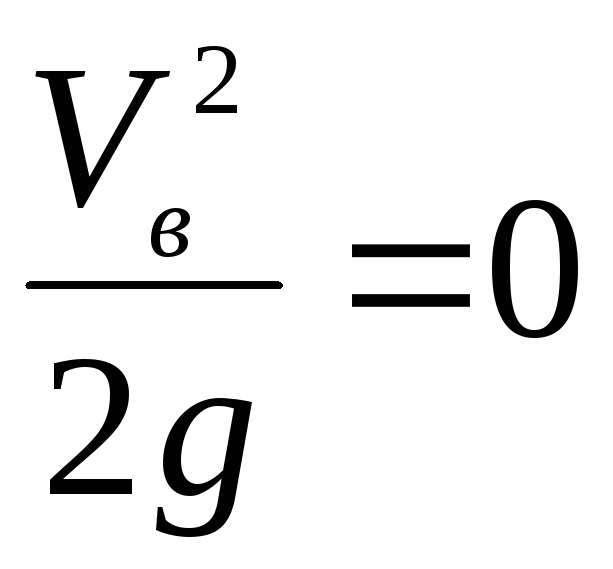 .
.
Скорость в сечении1-1
резервуара
считаем равной нулю, тогда
 .
.
Напор
 в сеченииВ-В
в сеченииВ-В
 . (5.23)
. (5.23)
Будем считать
трубопровод длинным, тогда
 и, следовательно, потери в нем можно
и, следовательно, потери в нем можно
определить по водопроводной формуле
(4.44):
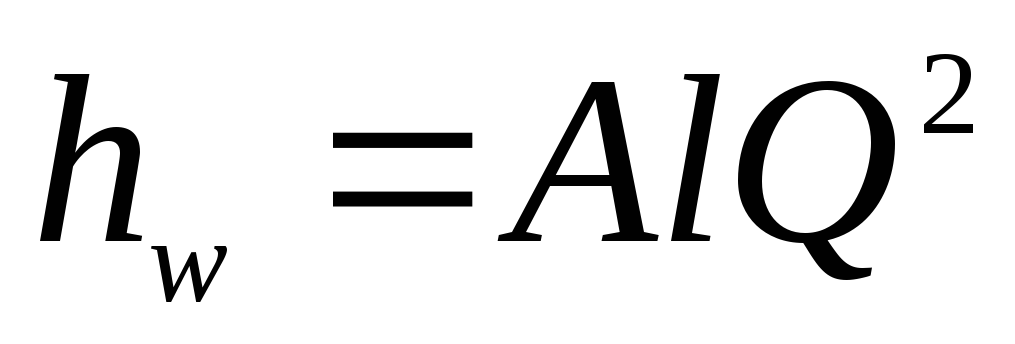 .
.
Напор в сечении
В-В
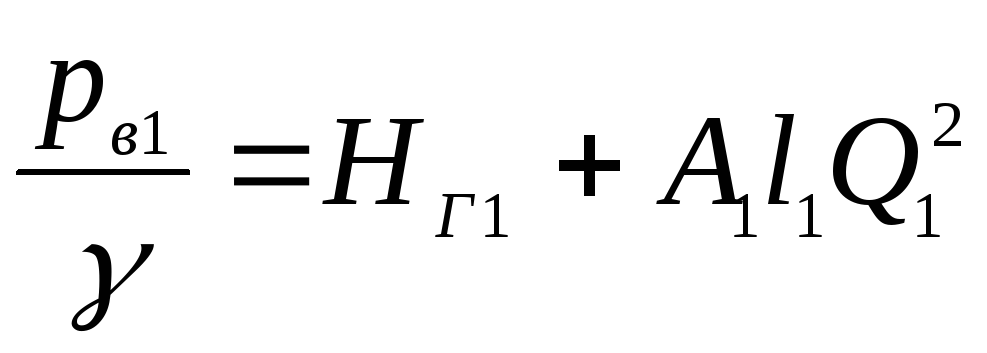 . (5.24)
. (5.24)
Аналогично,
рассматривая два других трубопровода,
можно получить:
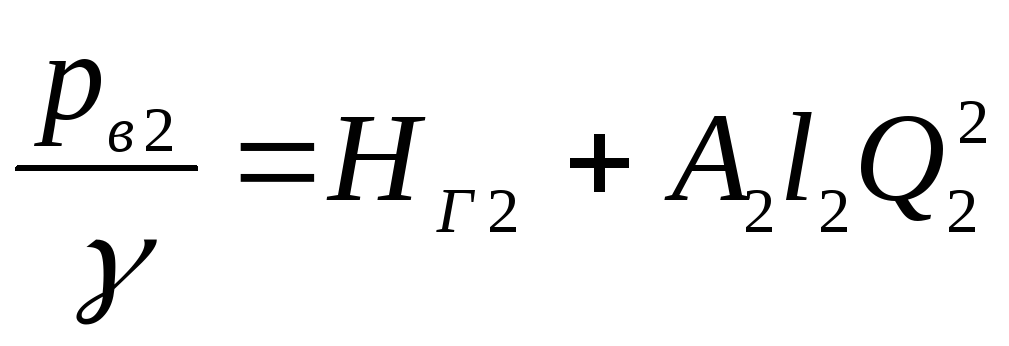 ; (5.25)
; (5.25)
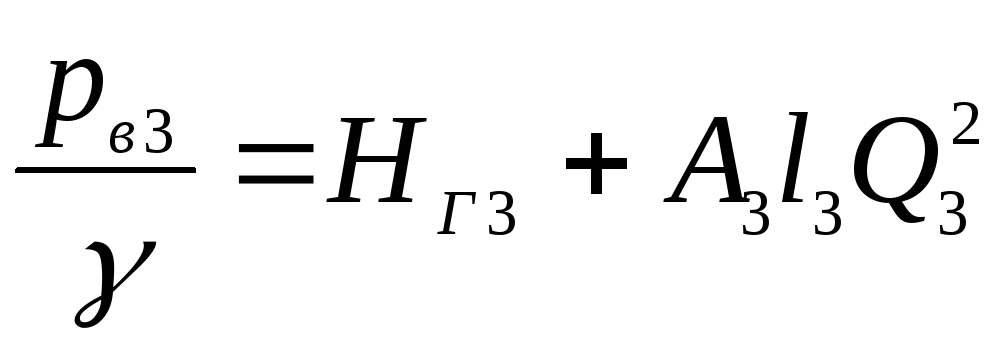
Таким образом, при
расчете простейшей схемы разветвленного
трубопровода используются полученные
уравнения (5.24) и (5.25), а также уравнение
(5.21). Совместное решение этих уравнений
позволяет определить все три расхода
—
 ,
, ,
,
 .
.
♦ Пример 5.5
Из водонапорной
башни в трубопровод (рис. 5.8), состоящий
из стальных труб, подается вода расходом
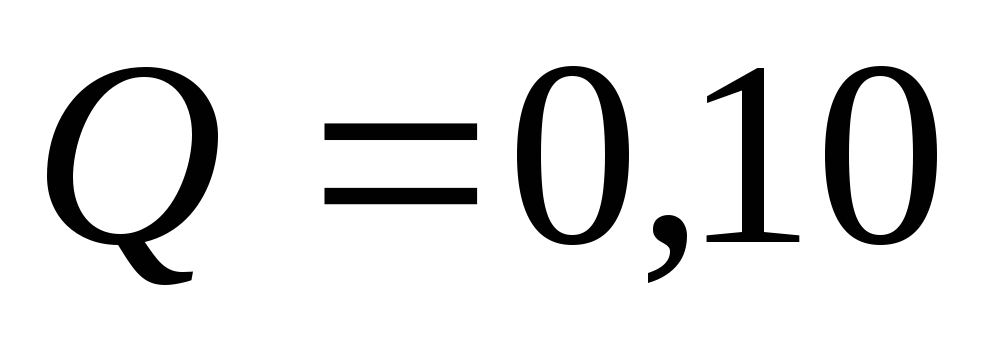 м3/с.
м3/с.
Длина трубы
до разветвления
 м, диаметр
м, диаметр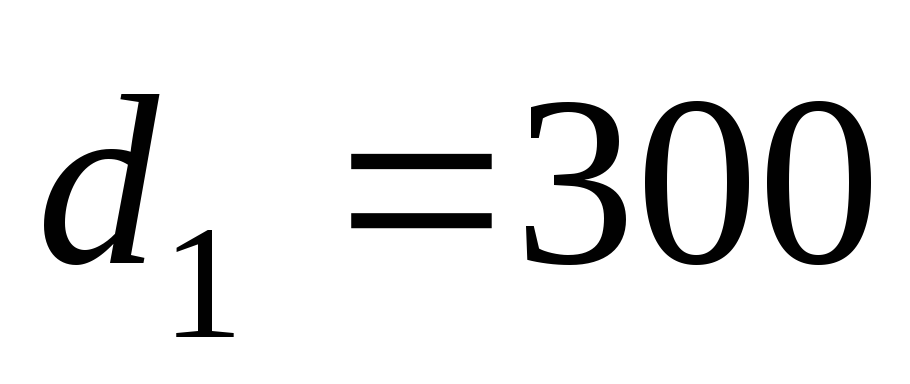 мм. В сеченииВ-В
мм. В сеченииВ-В
трубопровод
разветвляется на два трубопровода,
длины и диаметры которых соответственно
равны:
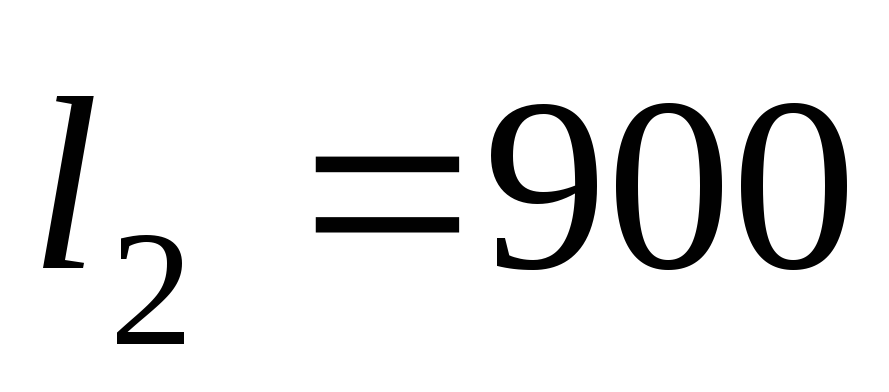 м,
м,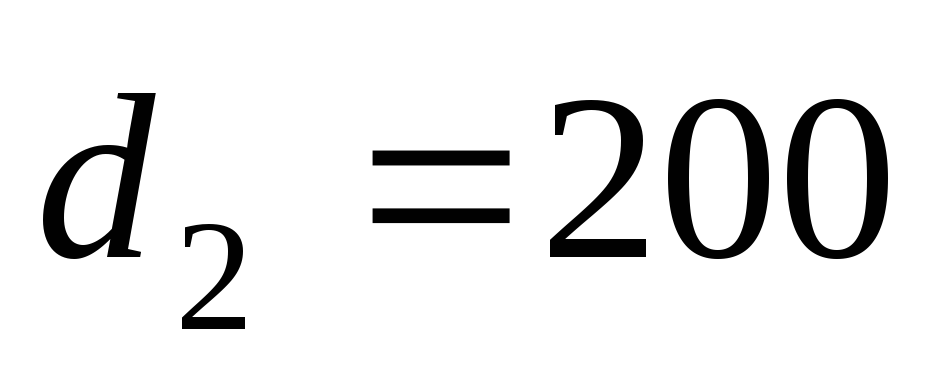 мм;
мм; м,
м,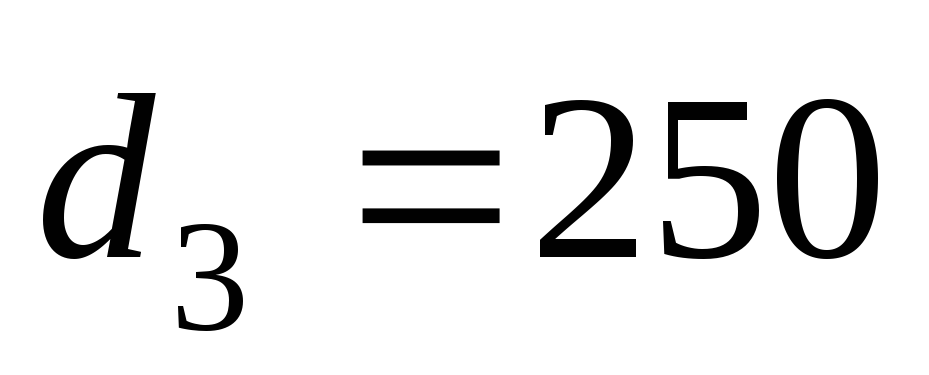 мм.
мм.
Определить расходы
в каждой ветви трубопровода. Геодезические
отметки подачи воды
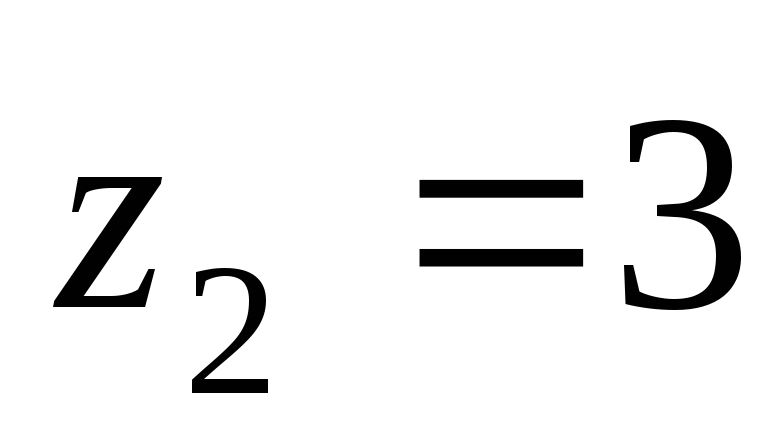 м и
м и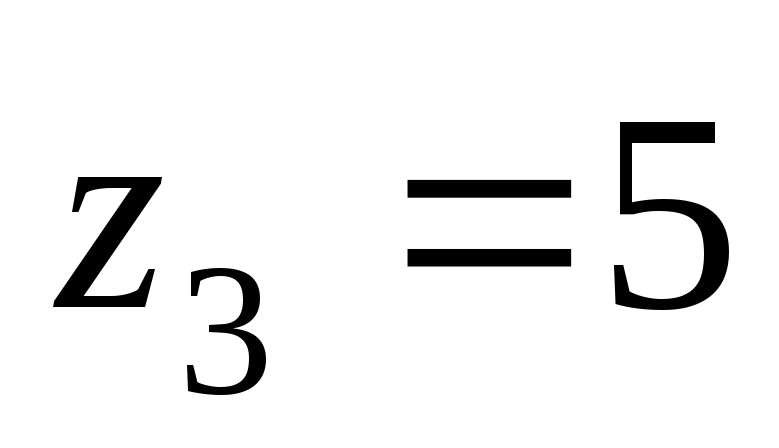 м.
м.
Расстояние от уровня воды в башне до
плоскости 0-0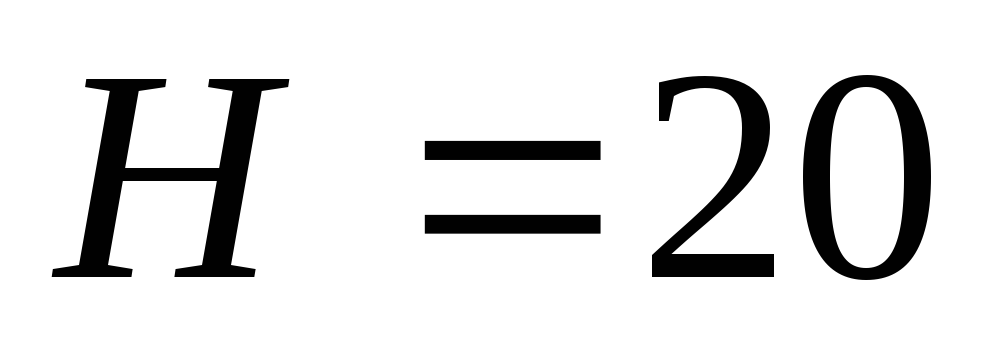 м. Местными сопротивлениями пренебречь.
м. Местными сопротивлениями пренебречь.
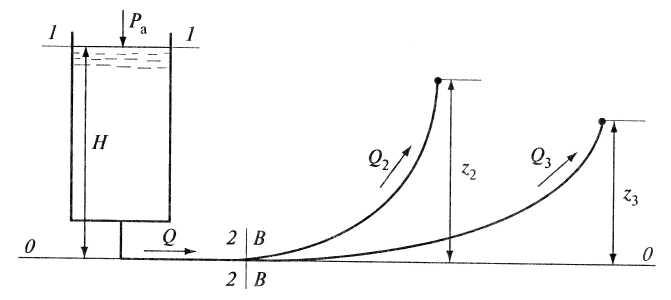
Рис.
5.8. К
примеру
5.5
Напор в сечении
В-В
определим,
используя уравнение Бернулли, приняв
плоскость сравнения 0-0. Первое сечение
совпадает со свободной поверхностью
воды водонапорной башни, второе сечение
— сечение В-В.
Принимаем
 ,
,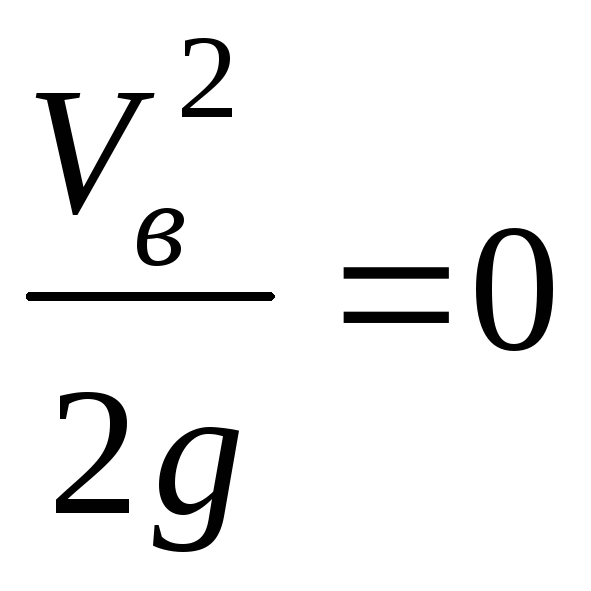 ,
,
согласно условию примера местные потери
равны нулю. Тогда из уравнения Бернулли
получим
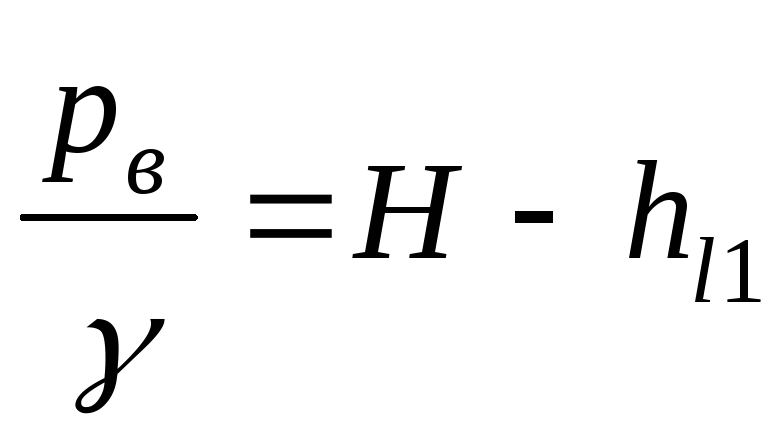 ,
,
где
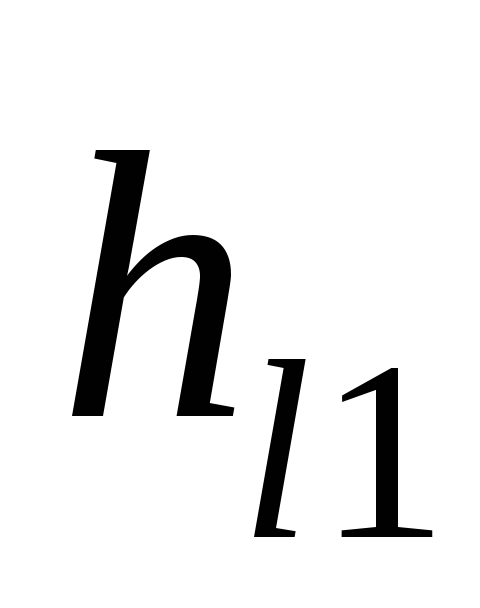
— гидравлические
потери по длине трубопровода до
разветвления.
По табл. 5.3 для
стальной трубы диаметром
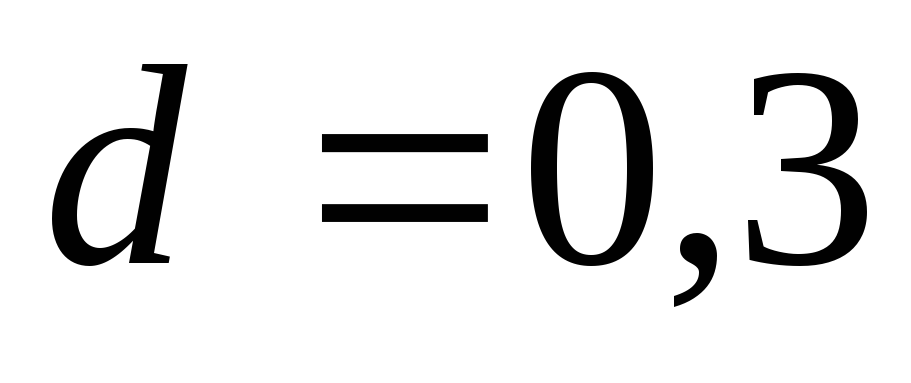 м находим удельное сопротивление
м находим удельное сопротивление с2/м6.
с2/м6.
Потери напора по длине
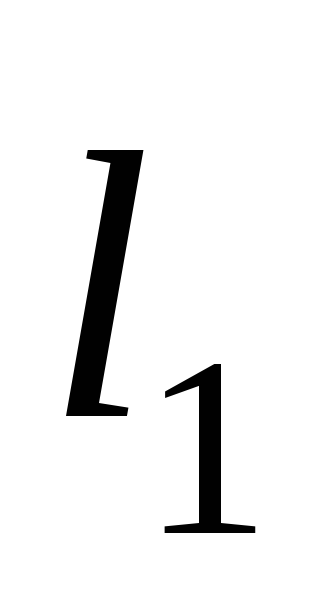 в трубопроводе при расходеQ
в трубопроводе при расходеQ
 м.
м.
Напор в сечении
В-В
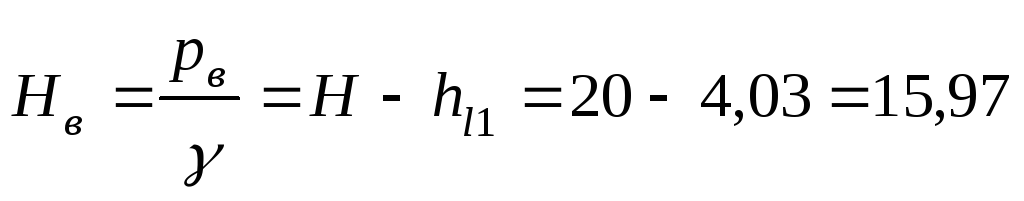 м.
м.
Согласно формуле
(5.25) напор в сечении
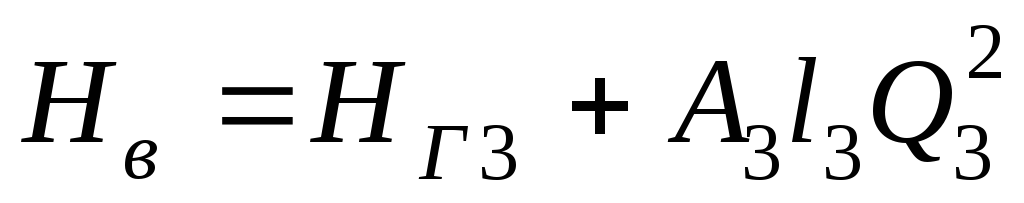 .
.
По табл. 5.3 для
трубы
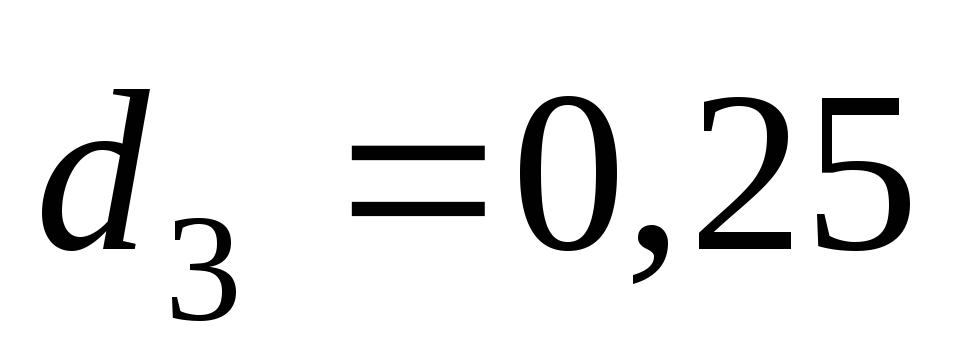 м находим
м находим с2/м6;
с2/м6;
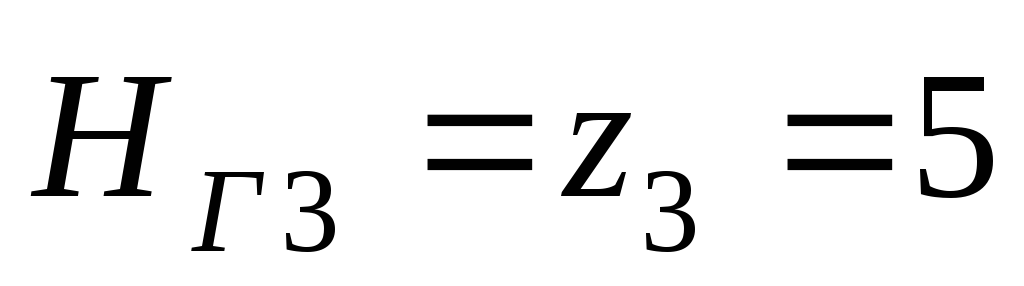 м.
м.
Расход в этом
трубопроводе
 м3/с.
м3/с.
Расход в трубопроводе
диаметром
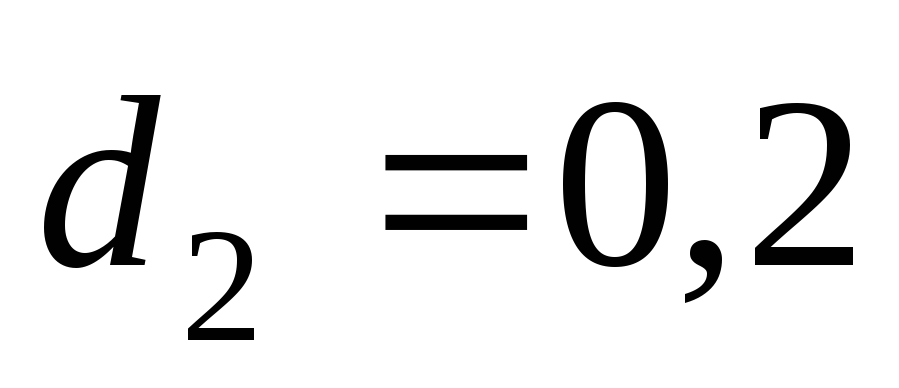 м
м
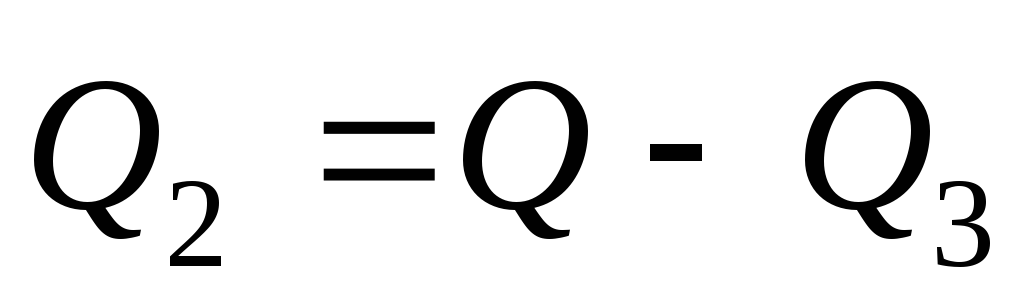 ;
;
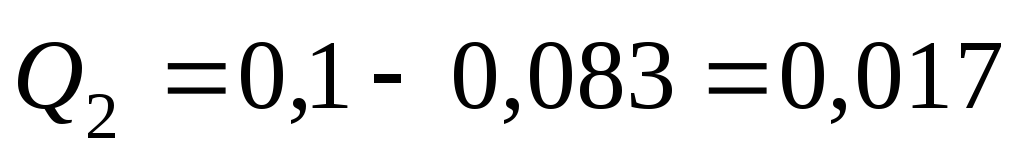 м3/с
м3/с
Параллельные
трубопроводы
Параллельными
трубопроводами
называются трубопроводы, которые имеют
свое начало в общем сечении и заканчиваются
в другом общем сечении.
На рис. 5.9 представлена
схема параллельного соединения трех
трубопроводов, имеющих разную длину и
диаметр.
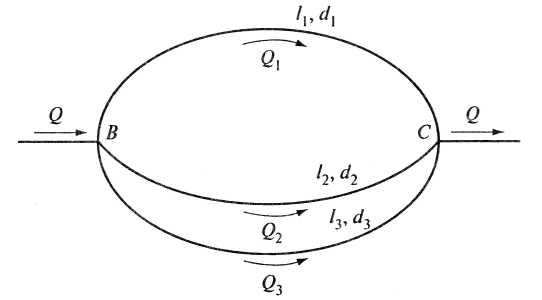
Рис.
5.9. Схема
параллельного
соединения
трех трубопроводов
В точке В
напор
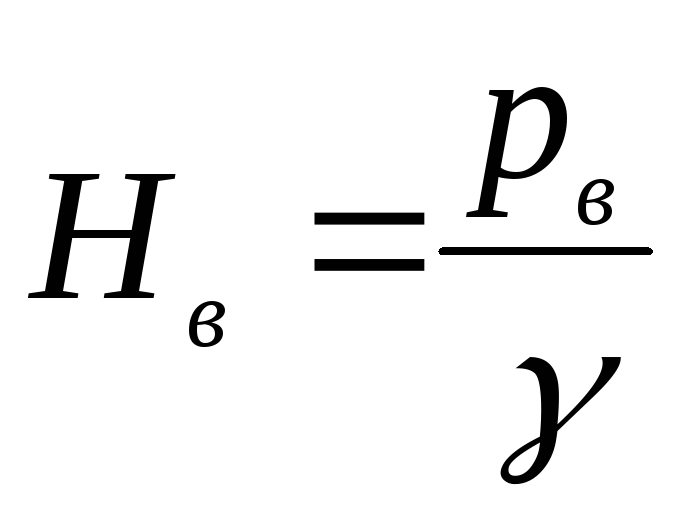 ,
,
а в точкеС
напор
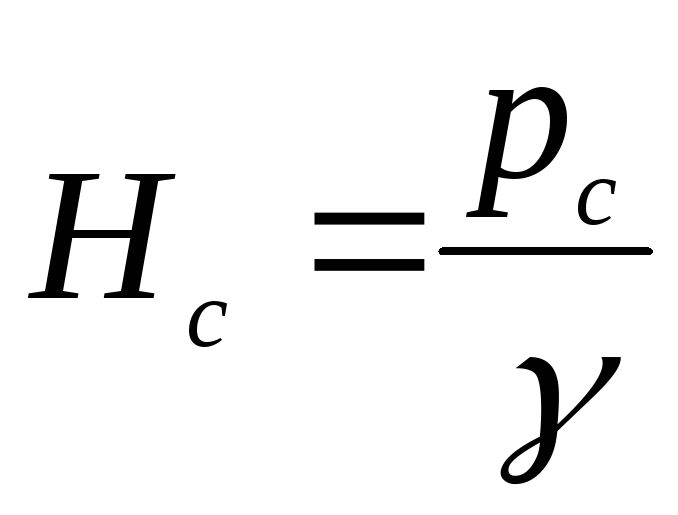 .
.
Расход до разветвления
(точка В)
равен сумме
расходов в трубах 1, 2 и 3:
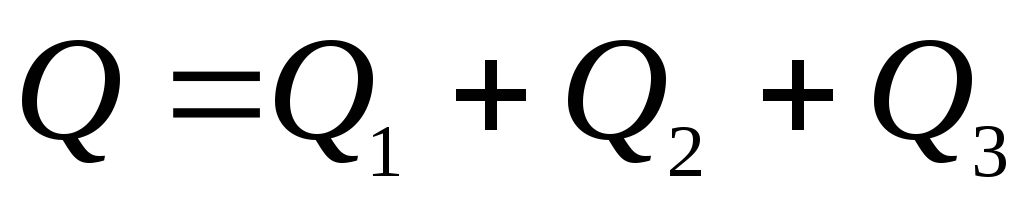 .
.
Разность
напоров в точках
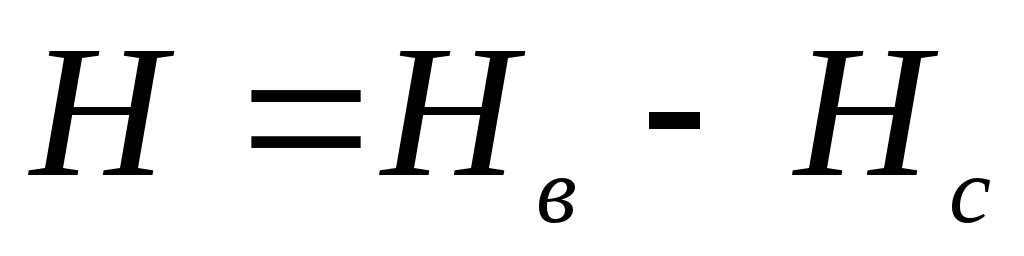 .
.
ТочкиВ
и С
принадлежат
всем трем трубопроводам. Разность
напоров в местах соединения труб
одинакова, следовательно, гидравлические
потери в каждой ветви трубопровода:
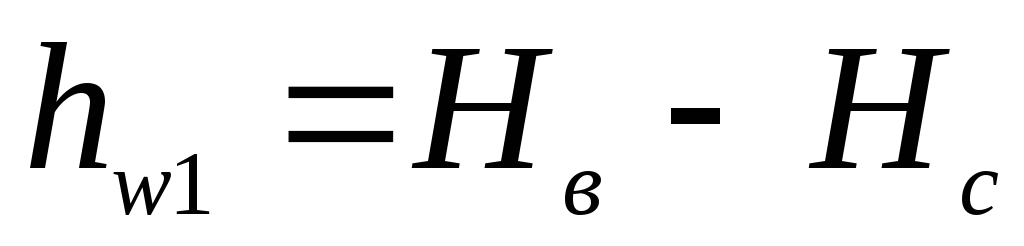 ;
;
 ; (5.26)
; (5.26)
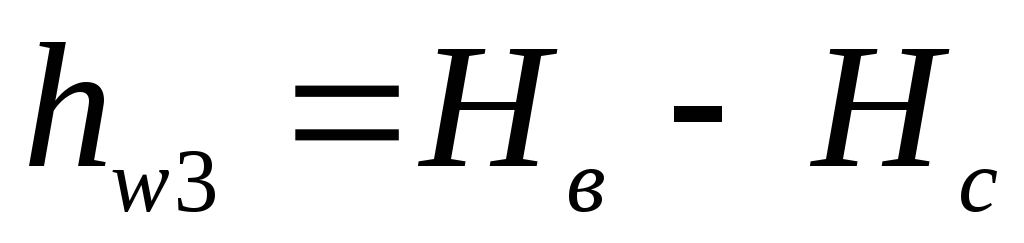 .
.
Таким образом,
можно считать, что гидравлические потери
во всех параллельно соединенных
трубопроводах независимо от их количества,
длины и диаметра одинаковые: 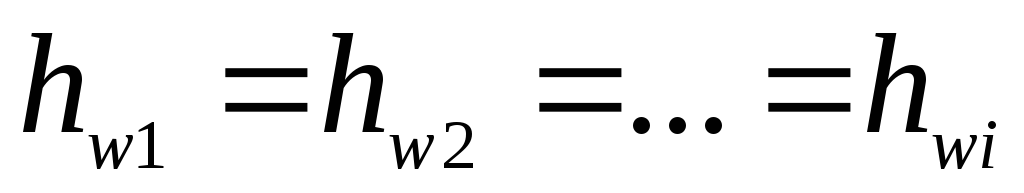 .
.
Полагая, что
местные гидравлические потери малы по
сравнению с потерями по длине и используя
водопроводную формулу (4.44), получим
систему уравнений:
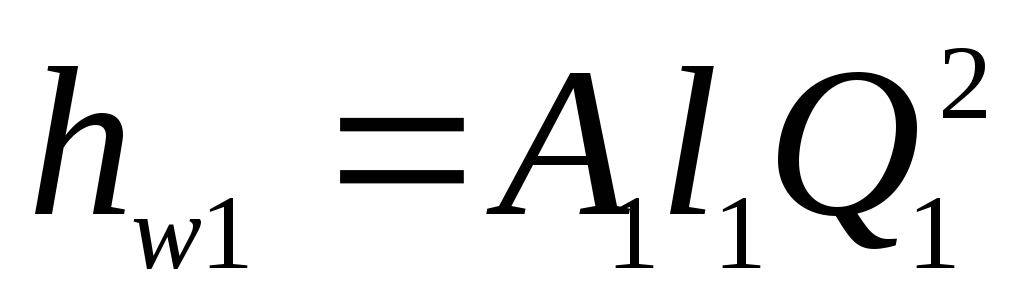 ;
;
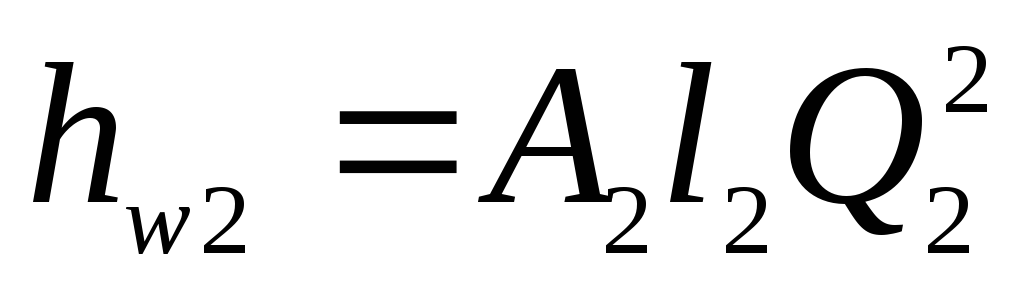 ; (5.27)
; (5.27)
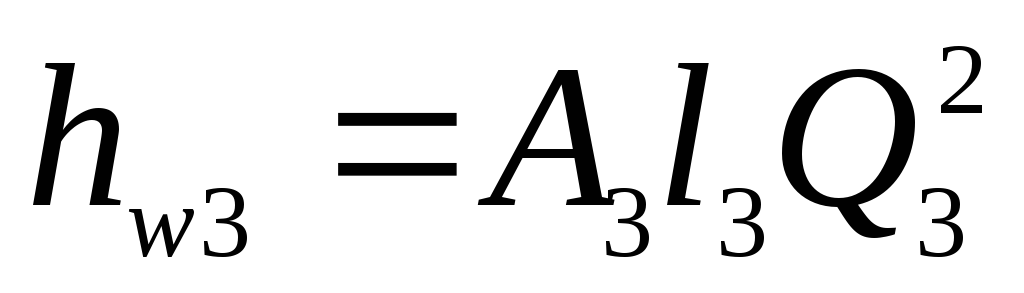 .
.
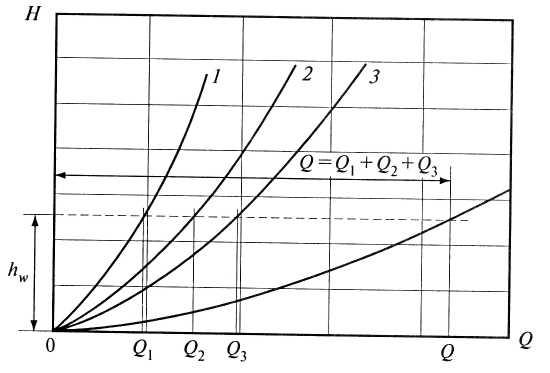
Рис.
5.10. Графики
характеристик
отдельных
параллельно
соединенных
трубопроводов
Расчет параллельно
соединенных трубопроводов заключается
в определении расходов в каждом из них
и основывается на использовании уравнений
(5.26) и (5.27). Количество уравнений
определяется числом трубопроводов,
присоединенных к сечениям В
и С.
Используя эти
уравнения, можно построить графики
функций характеристик отдельных
трубопроводов
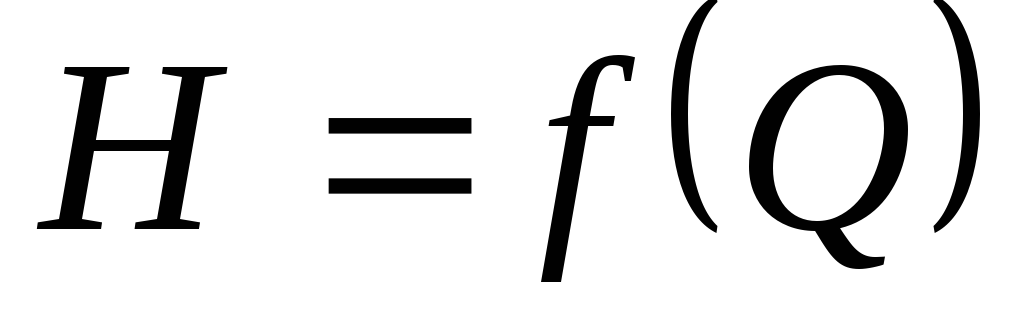
(рис. 5.10).
Для удобства
построения графиков можно применить
параметр
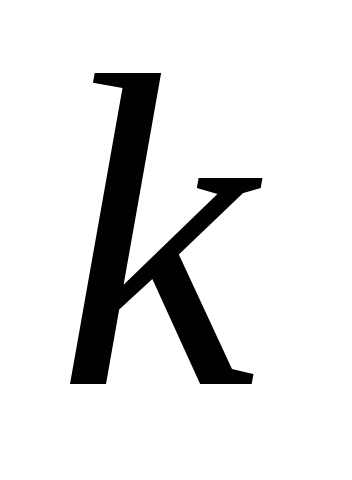
(сопротивление
трубопровода):
 ;
;
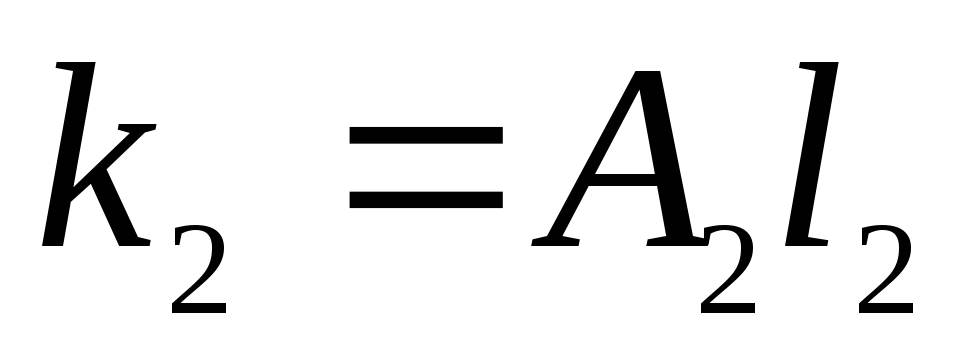 ;
;
 и т.д.
и т.д.
Зависимость
гидравлических потерь имеет следующий
вид:
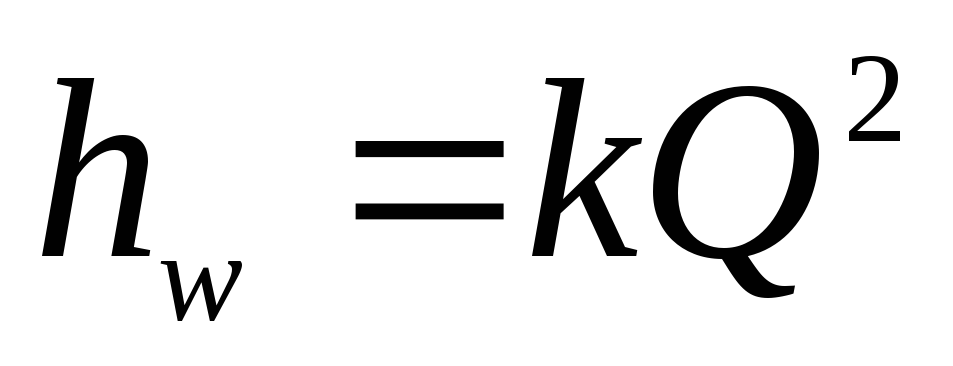 .
.
Характеристика
параллельно соединенного трубопровода
строится путем сложения по горизонтали
расходов
 при одинаковых
при одинаковых .
.
♦ Пример 5.6
На водоводе между
точками В
и С
установлены три параллельных трубопровода
(см. рис. 5.9). Расход в водоводе до
разветвления
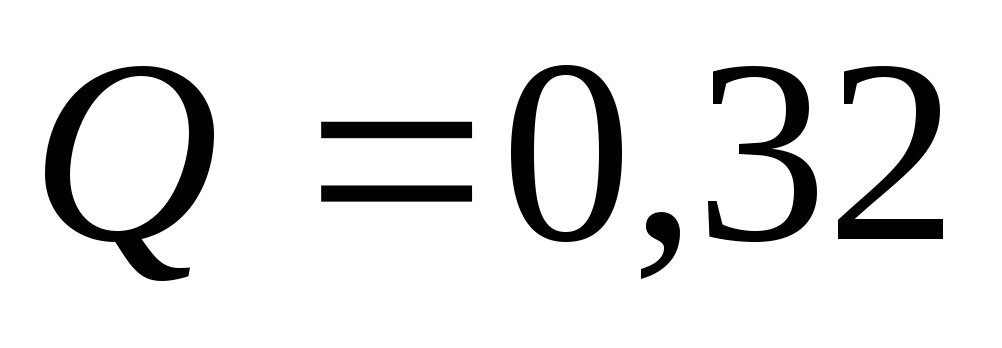 м3/с
м3/с
Длины и диаметры трубопроводов:
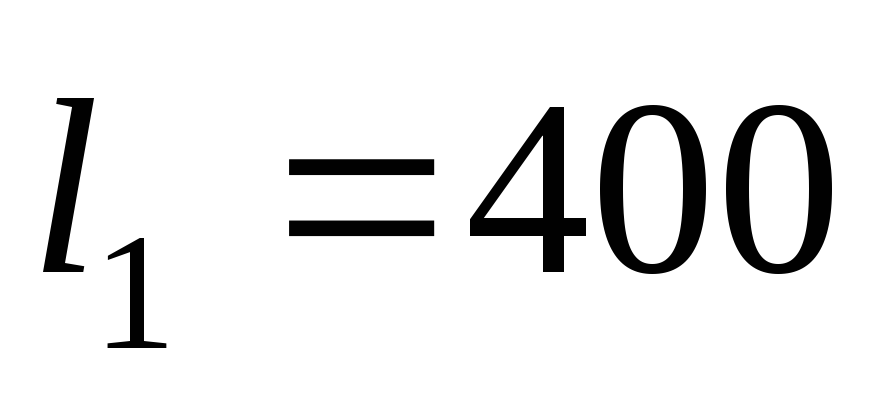 м,
м,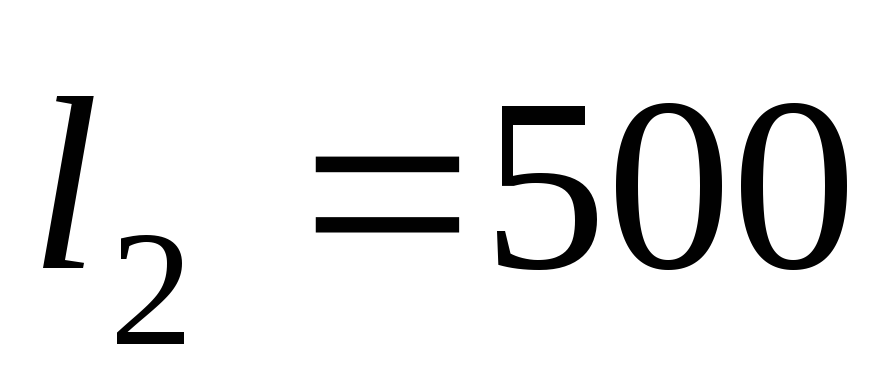 м,
м,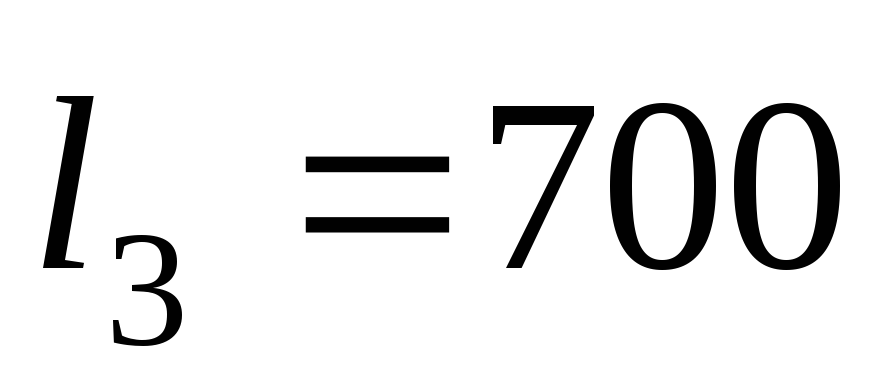 м;
м;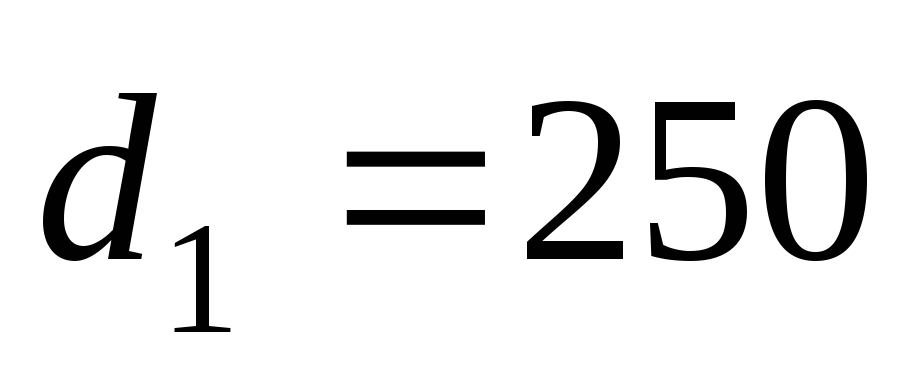 мм,
мм,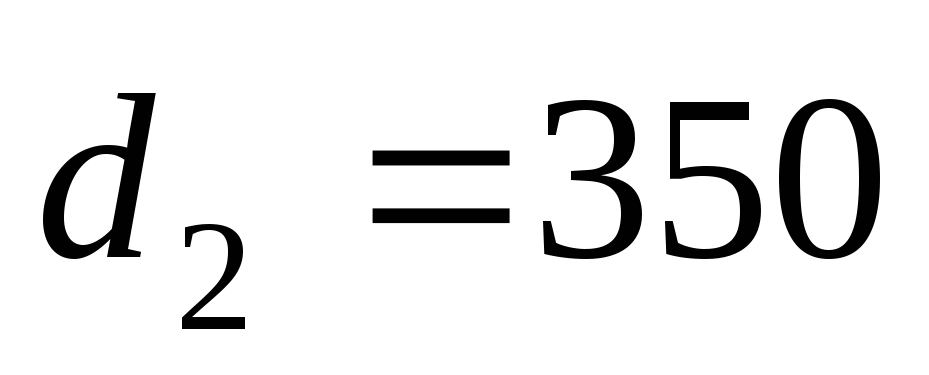 мм,
мм,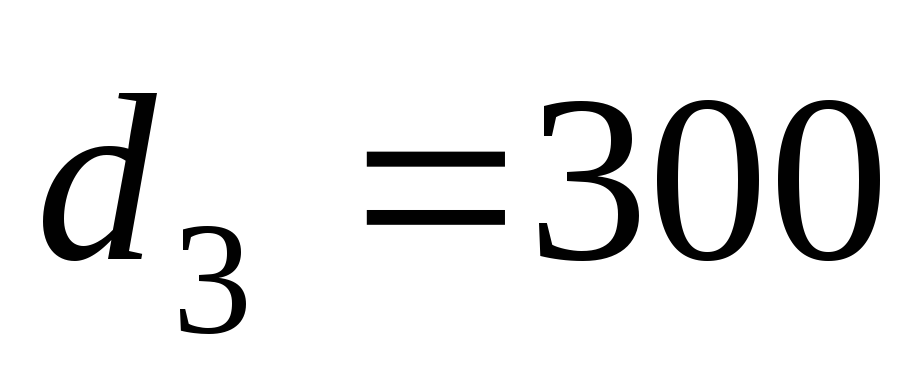 мм. Определить расходы в отдельных
мм. Определить расходы в отдельных
стальных трубопроводах и потери напора
между точкамиВ
и С.
Гидравлические
потери в трубопроводах 1, 2 и 3
 .
.
По табл. 5.3 находим
значения удельных сопротивлений для
стальных труб:
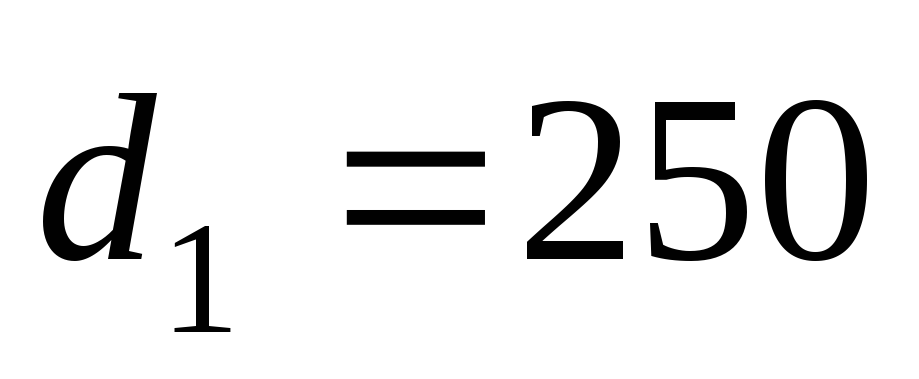 мм,
мм, 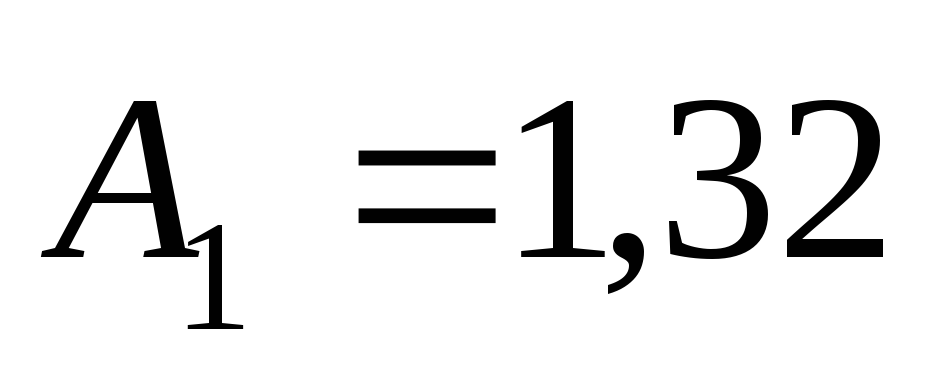 с2/м6;
с2/м6;
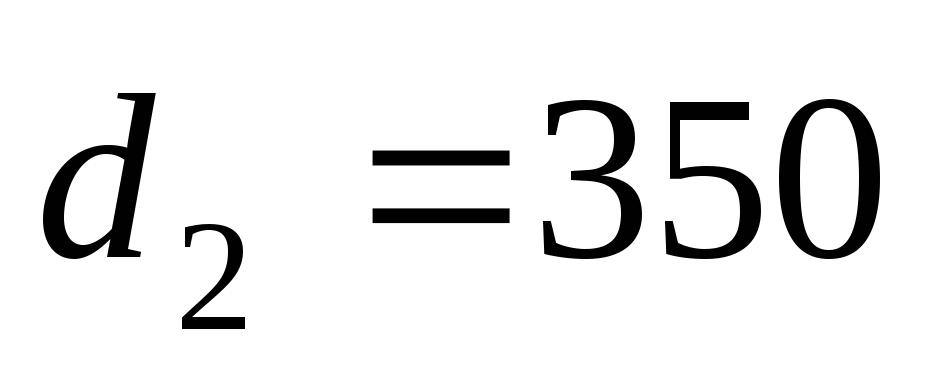 мм,
мм,  с2/м6;
с2/м6;
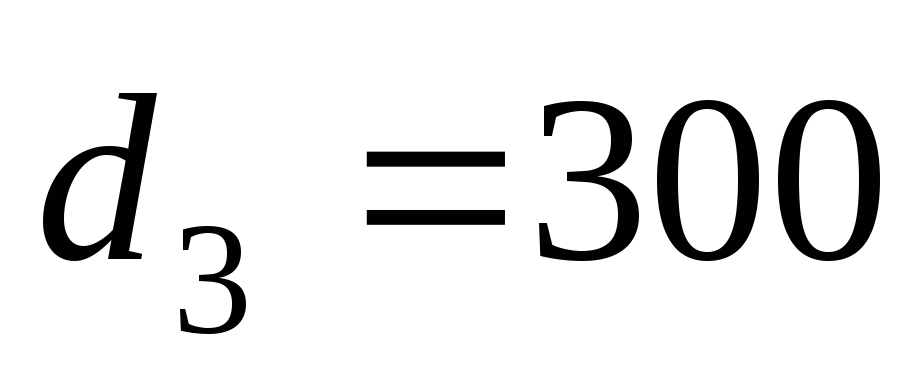 мм,
мм, 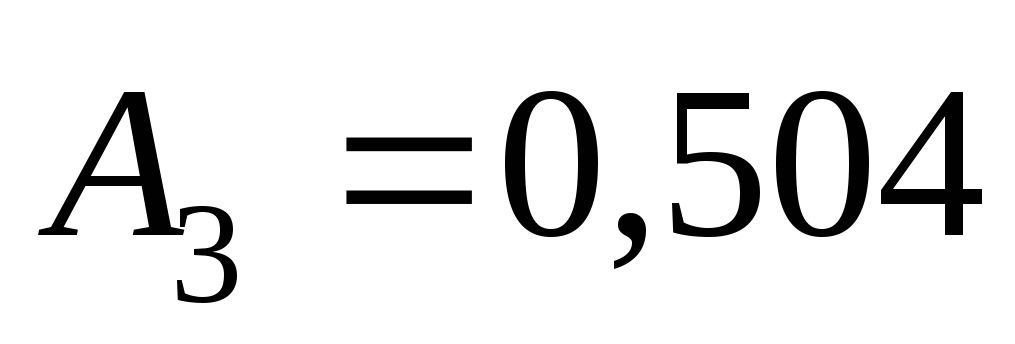 с2/м6.
с2/м6.
Выразим
и через
через ,
,
используя
равенство потерь напора в трубопроводах,
получим:
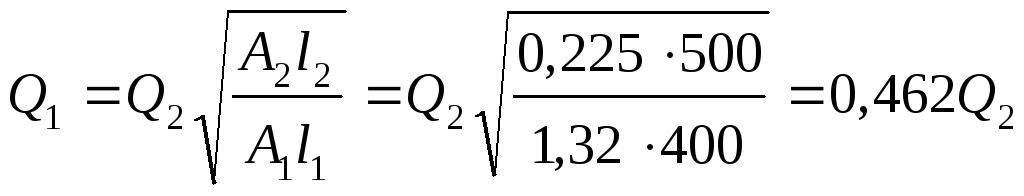 ;
;
 .
.
Расход в водоводе
равен сумме расходов в трубопроводах:
 .
.
Расход во втором
трубопроводе
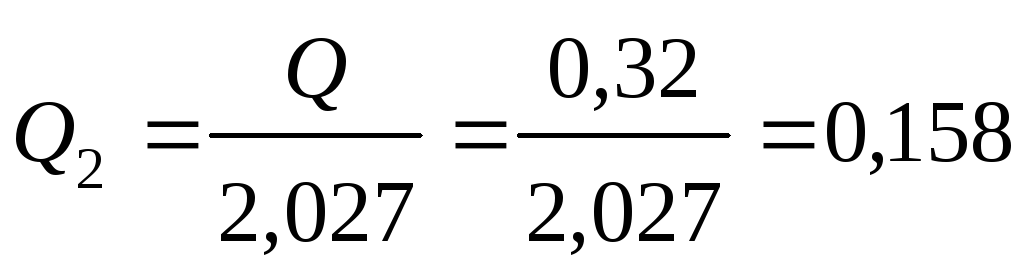 м3/с.
м3/с.
В первом трубопроводе
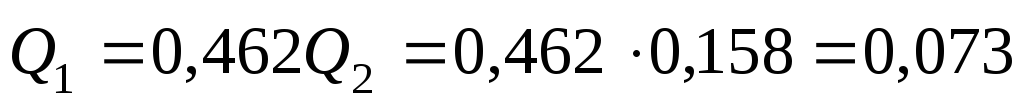 м3/c.
м3/c.
В третьем трубопроводе
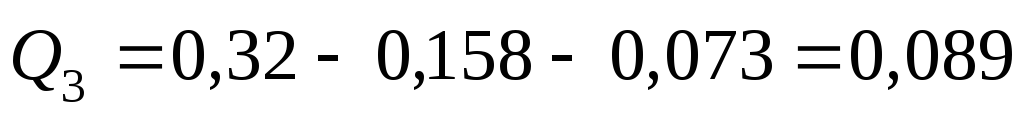 м3/с
м3/с
Потери напора
между точками В
и С
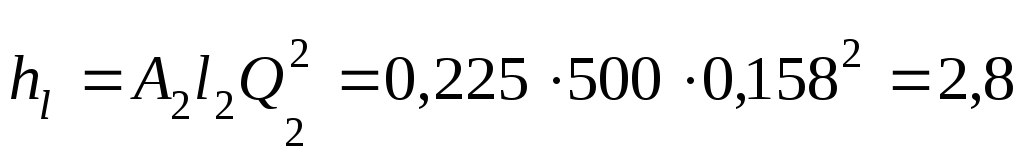 м.
м.
9. Гидравлический расчет сложного разветвленного трубопровода Содержание работы
1. Теоретическая часть.
Принципы
гидравлического расчета сложных
трубопроводов. Расчет трубопроводов,
соединенных последовательно и параллельно.
2. Расчетная часть.
Заданы
напоры в конечных пунктах разветвленной
водопроводной сети (в пунктах потребления),
линейные размеры трубопровода (диаметры
участков, их длины и шероховатости
труб). Известна также скорость течения
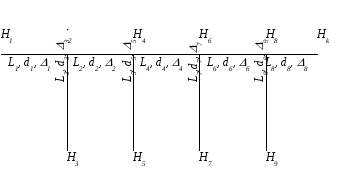
в конечном пункте потребления. Схема
трубопровода приведена на рисунке.
Вязкость жидкости считается известной
и постоянной по всей длине трубопровода.
Все исходные данные приведены в таблице.
Определить
напоры H2,
H4,
H6
и H8
в узловых точках и начальный напор H1.Найти
расходы и скорости течения на всех
участках разветвленного трубопровода.Рассчитать
изменение всех искомых параметров при
изменении скорости vК
в конечном пункте потребления.Построить
характеристику трубопровода Н
= Н(Q).
Методические указания
Потерями энергии
в местных сопротивлениях пренебречь
По
известной скорости vК
в конечном пункте потребления вычисляется
число Рейнольдса Re
и определяется режим течения жидкости.
Рассчитываются потери напора на участке
длиной L8,
по известному напору HK
находят
напор H8.
Зная
напоры H8
и H9,
определяют потери напора.
Расход
на этом участке трубопровода определяется
графоаналитическим методом. В результате
решения находят расход и скорость на
этом участке. Если H9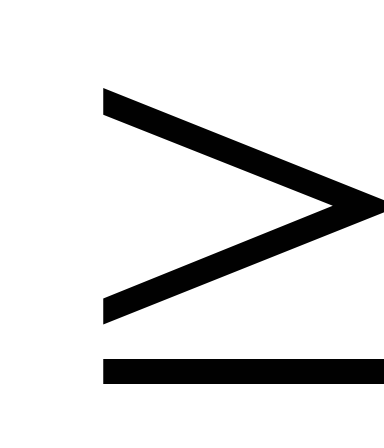 H8,
H8,
то Q9
= 0.
Определяют
неизвестные расходы и скорости на всех
участках трубопровода.
Изменяют
скорость течения vК
в конечном пункте потребления и определяют
все требуемые параметры: расходы и
скорости на всех участках, а также напоры
в узловых точках.
В
выводах указать возможные пути повышения
расхода трубопровода и отдельных его
участков.
Исходные данные
Величины | Варианты | ||||
H3, | 5 | 10 | 15 | 20 | 10 |
H5, | 5 | 10 | 15 | 20 | 10 |
H7, | 5 | 10 | 15 | 20 | 10 |
H9, | 5 | 10 | 15 | 20 | 10 |
, | 21,8 | 7,64 | 11,0 | 25,7 | 15,0 |
vК, | 0,2-0,3 | 0,3-0,4 | 0,4-0,5 | 0,15-0,3 | 0,1-0,2 |
Hк, | 5 | 10 | 15 | 20 | 10 |
Для
вариантов 1-5
Величины | Участки | ||||||||
d, | 402 | 402 | 180 | 402 | 156 | 402 | 136 | 402 | 156 |
L, | 700 | 600 | 300 | 800 | 400 | 700 | 600 | 1200 | 200 |
∙10-2, | 15 | 15 | 17 | 15 | 17 | 15 | 6 | 15 | 6 |
Схема
трубопровода
55.1 Гидравлический расчет простых трубопроводов.
Жидкость
по трубопроводу движется благодаря
тому, что ее энергия в начале трубопровода
больше, чем в конце. Этот перепад уровней
энергии может создаваться несколькими
способами: работой насоса, разностью
уровней жидкости, давлением газа.
Рассмотрим простой трубопровод
постоянного сечения, который расположен
произвольно в пространстве (рис.), имеет
общую длину  и
и
диаметр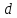 ,
,
а также содержит ряд местных сопротивлений
(вентиль, фильтр и обратный клапан). В
начальном сечении трубопровода 1-1 геометрическая
высота равна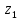 и
и
избыточное давление ,
,
а в конечном сечении 2-2 —
соответственно и
и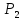 .
.
Скорость потока в этих сечениях вследствие
постоянства диаметра трубы одинакова
и равна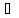 .
.
Запишем уравнение Бернулли для
сечений 1-1 и 2-2. Поскольку скорость
в обоих сечениях одинакова и ,
,
то скоростной напор можно не учитывать.
При этом получим или
или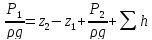 .
.
Пьезометрическую высоту, стоящую в
левой части уравнения, назовем потребным
напором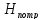 .
.
Если же эта пьезометрическая высота
задана, то ее называют располагаемым
напором .
.
Такой напор складывается из геометрической
высоты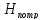 ,
,
на которую поднимается жидкость,
пьезометрической высоты в конце
трубопровода и суммы всех потерь напора
в трубопроводе. Назовем сумму первых
двух слагаемых статическим напором,
который представим как некоторую
эквивалентную геометрическую высоту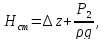 а
а
последнее слагаемое —
—
как степенную функцию расхода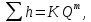 тогда
тогда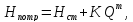
где
 —
—
величина, называемая сопротивлением
трубопровода;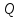 —
—
расход жидкости;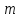 —
—
показатель степени, который имеет разные
значения в зависимости от режима течения.
Для ламинарного течения при замене
местных сопротивлений эквивалентными
длинами сопротивление трубопровода
равно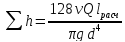 ,
,
следовательно,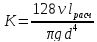 и
и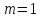 ,
,
где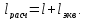 Численные
Численные
значения эквивалентных длин для
для
различных местных сопротивлений обычно
находят опытным путем. Для турбулентного
течения, используя формулу Вейсбаха-Дарси,
и выражая в ней скорость через расход,
получаем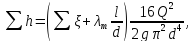 следовательно,
следовательно,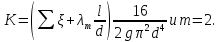 По
По
этим формулам можно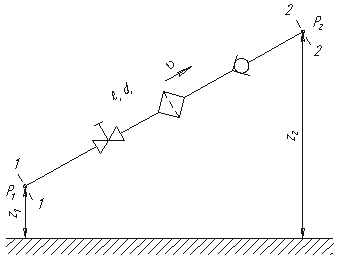
55.2 Гидравлический расчет простых трубопроводов.
построить
кривую потребного напора в зависимости
от расхода. Чем больше расход 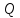 ,
,
который необходимо обеспечить в
трубопроводе, тем больше требуется
потребный напор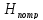 .
.
При ламинарном течении эта кривая
изображается прямой линией (а), при
турбулентном — параболой с показателем
степени равном двум (б). Крутизна кривых
потребного напора зависит от сопротивления
трубопровода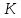 и
и
возрастает с увеличением длины
трубопровода и уменьшением диаметра,
а также с увеличением местных гидравлических
сопротивлений.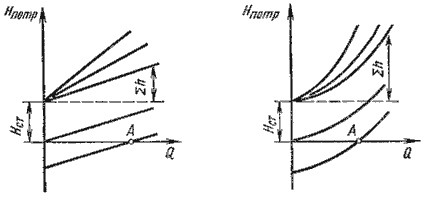
Величина
статического напора  положительна
положительна
в том случае, когда жидкость движется
вверх или в полость с повышенным
давлением, и отрицательна при опускании
жидкости или движении в полость с
пониженным давлением. Точка пересечения
кривой потребного напора с осью абсцисс
(точка А) определяет расход при
движении жидкости самотеком. Потребный
напор в этом случае равен нулю. Иногда
вместо кривых потребного напора удобнее
пользоваться характеристиками
трубопровода. Характеристикой
трубопровода называется зависимость
суммарной потери напора (или давления)
в трубопроводе от расхода: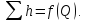
3. Гидравлический расчет коротких трубопроводов
Рассмотрим
установившееся движение жидкости в
напорных трубопроводах при постоянном
напоре.
При
движении реальных жидкостей в трубопроводах
происходят потери напора (удельной
энергии), которые в соответствии с
законом наложения сопротивлений
определяются между двумя расчетными
сечениями 1-1 и 2-2 как сумма:
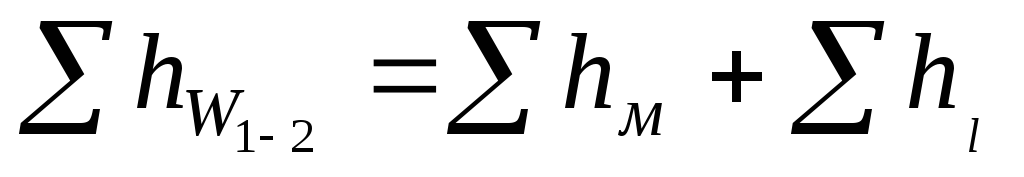 , (3.1)
, (3.1)
где 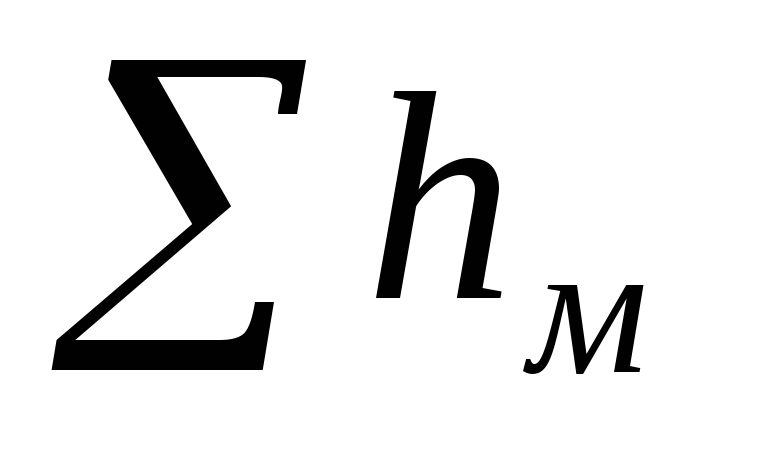 — сумма потерь напора на преодоление
— сумма потерь напора на преодоление
местных сопротивлений;
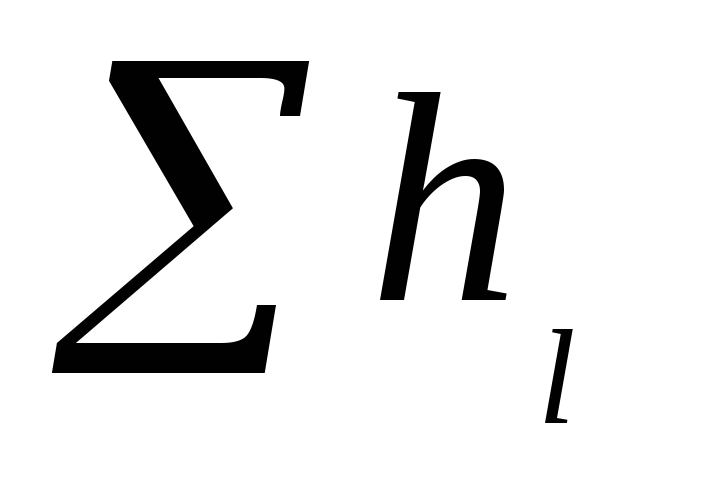 — сумма потерь напора по длине (на трение).
— сумма потерь напора по длине (на трение).
Все
трубопроводы, работающие в напорном
гидравлическом режиме, по принятой
классификации делят на три вида:
1.
Насадки
— весьма короткие трубы, длина которых
находится в пределах
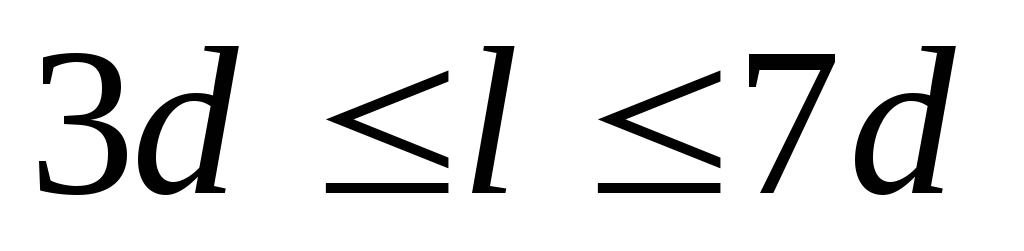 . (3.2)
. (3.2)
При
гидравлическом расчете насадков
учитываются только местные потери
напора, потерями напора по длине ввиду
их малости пренебрегают.
2.
Короткие
трубопроводы
— трубопроводы, в которых местные потери
напора и потери по длине сопоставимы
по значению, поэтому при гидравлическом
расчете коротких трубопроводов
учитываются все потери напора как
местные, так и по длине.
3.
Длинные
трубопроводы —
трубопроводы, в которых потери напора
по длине настолько превышают местные
потери, что последними, ввиду малости,
пренебрегают или учитывают долей в
общих потерях, увеличивая найденные
значения потерь напора по длине на 5-10
%.
Главнейшими
уравнениями, которые применяются для
расчета насадков и коротких трубопроводов,
являются:
1)
уравнение Бернулли для целого потока
реальной жидкости;
2)
уравнение неразрывности или баланса
расхода;
3)
уравнения для определения потерь напора.
В
зависимости от исходных данных и методики
расчета коротких трубопроводов различают
три типа
задач:
1)
определение напора
 ,
,
необходимого для пропуска расчетного
расхода в трубопроводе заданных размеров;
2)
определение расхода
 при расчетном напоре
при расчетном напоре в заданном трубопроводе;
в заданном трубопроводе;
3)
определение диаметра
 трубопровода, обеспечивающего пропуск
трубопровода, обеспечивающего пропуск
расчетного расхода при заданном напоре
при заданном напоре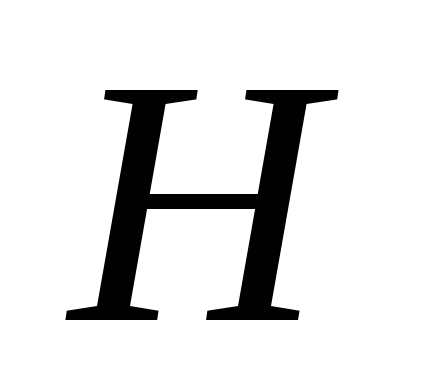 .
.
Часто
в числе задач гидравлического расчета
коротких трубопроводов требуется
выполнить построение напорной (линии
удельной энергии) и пьезометрической
линий.
Следует
отметить, что с гидравлической точки
зрения к коротким трубопроводам (трубам)
относятся все сооружения трубчатой
конструкции, работающие в напорном
гидравлическом режиме.
Основным
уравнением гидродинамики, устанавливающим
связь между основными характеристиками
потока — скоростью, давлением в двух
выбранных сечениях 1-1 и 2-2, является
уравнение Бернулли:
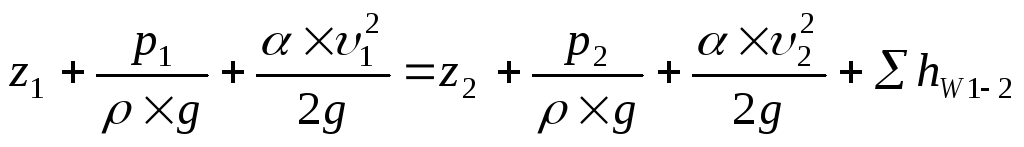 . (3.3)
. (3.3)
Каждый
член, входящий в уравнение Бернулли, с
геометрической
и энергетической
точек зрения имеет определенный смысл.
Геометрическая интерпретация уравнения Бернулли:
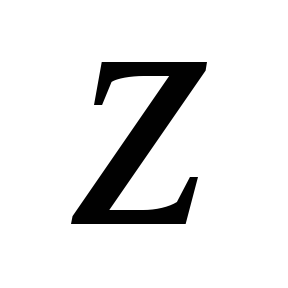 —
—
высота положения, произвольно выбранной
в рассматриваемом живом сечении, точки
относительно любой горизонтальной
плоскости сравнения 0 — 0; за характерную
точку в большинстве случаев принимается
центр тяжести сечения и тогда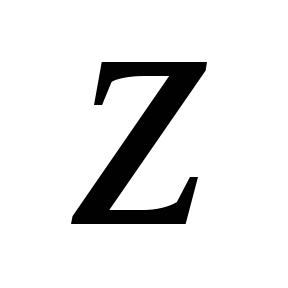 — высота положения сечения над плоскостью
— высота положения сечения над плоскостью
сравнения (геодезическая высота),
определяется расстоянием от плоскости
сравнения до центра тяжести сечения;
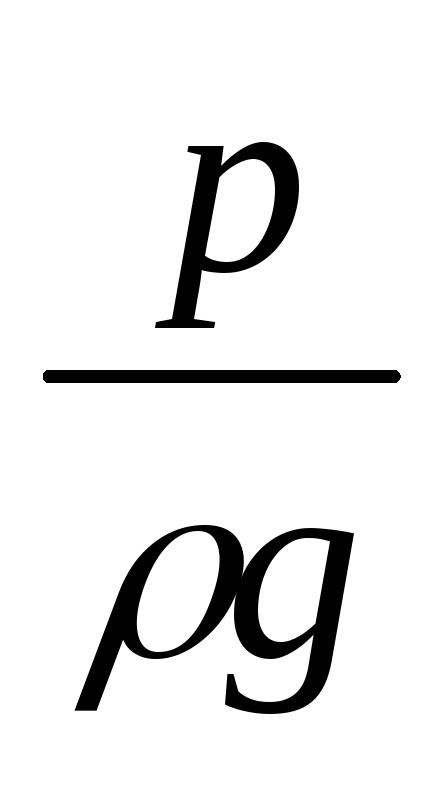 — пьезометрическая высота, соответствующая
— пьезометрическая высота, соответствующая
избыточному давлению в точке;
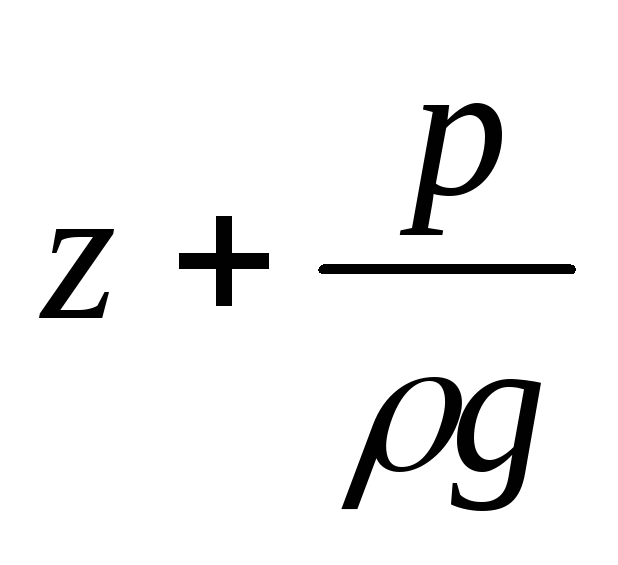 пьезометрический
пьезометрический
напор;
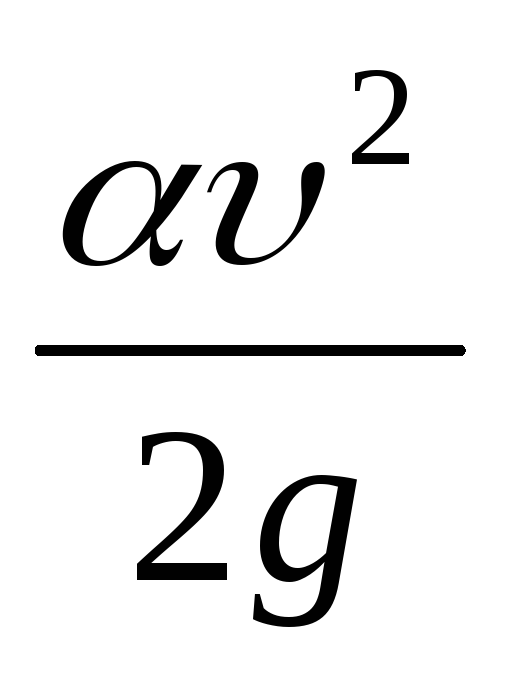
— скоростной напор;
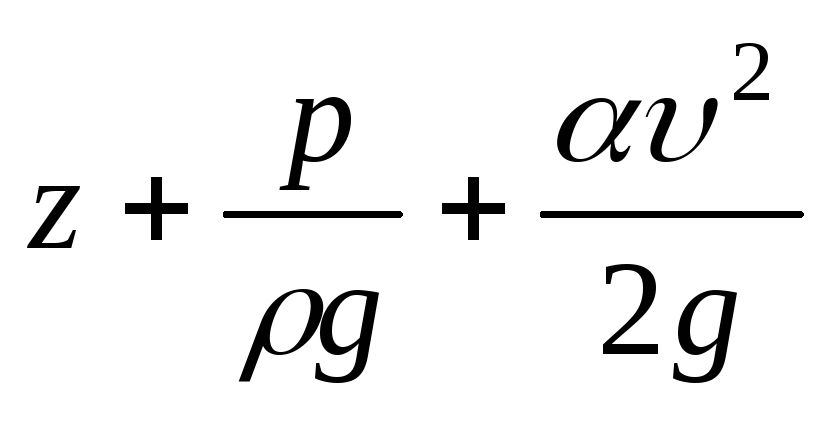 гидродинамический
гидродинамический
напор;
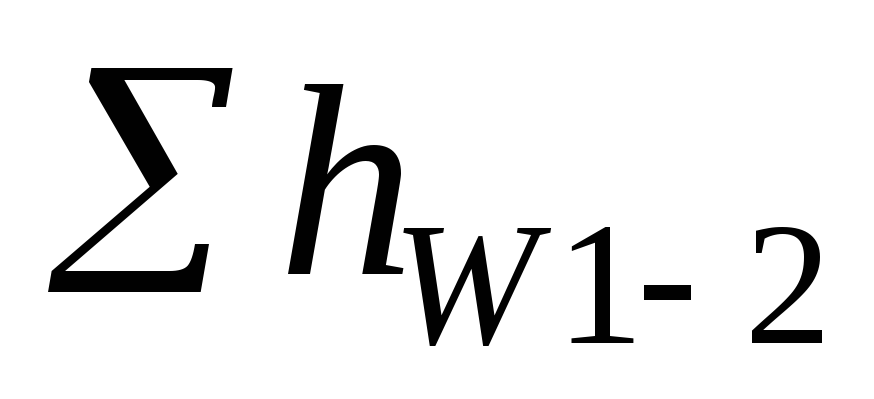 —
—
 потери
потери
напора.
Гидравлические расчеты трубопроводов. Расчет диаметра трубопровода. Подбор трубопроводов
Пример № 1
Каковы потери напора на местные сопротивления в горизонтальном трубопроводе диаметром 20 х 4 мм, по которому вода перекачивается из открытого резервуара в реактор с давлением 1,8 бар? Расстояние между резервуаром и реактором 30 м. Расход воды 90 м3 / час. Общий напор равен 25 м. Коэффициент трения принимается равным 0.028.

Решение:
Скорость потока воды в трубопроводе равна:
w = (4 · Q) / (π · d 2 ) = ((4 · 90) / (3,14 · [0,012] 2 )) · (1/3600) = 1,6 м / с
Находим потери на трение напора в трубопроводе:
H Т = (λ · l) / (d э · [w 2 / (2 · g)]) = (0,028 · 30) / (0,012 · [1,6] 2 ) / ((2 · 9,81)) = 9,13 м
Всего потерь:
ч п = H — [(p 2 -p 1 ) / (ρ · г)] — H г = 25 — [(1,8-1) · 10 5 ) / (1000 · 9,81)] — 0 = 16,85 м
Убытки на локальном сопротивлении находятся в пределах:
16,85-9,13 = 7,72 м
Пример №2
Вода перекачивается центробежным насосом по горизонтальному трубопроводу со скоростью 1,5 м / с. Суммарный создаваемый напор равен 7 м. Какова максимальная длина трубопровода, если вода берется из открытого резервуара, перекачивается по горизонтальному трубопроводу с одной задвижкой и двумя коленами на 90 ° и вытекает из трубы в другой резервуар? Диаметр трубопровода 100 мм. Относительная шероховатость принята равной 4 · 10 -5 .
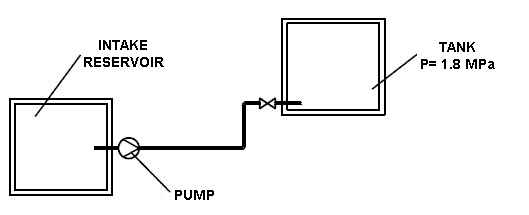
Решение:
Для трубы диаметром 100 мм коэффициенты местных сопротивлений будут равны:
Для колена 90 ° — 1.1; задвижка — 4,1; выход трубы — 1.
Затем определяем значение скоростного напора:
w 2 / (2 · g) = 1,5 2 / (2 · 9,81) = 0,125 м
Потери напора на местные сопротивления будут равны:
∑ζ МС · [w 2 / (2 · g)] = (2 · 1,1 + 4,1 + 1) · 0,125 = 0,9125 м
Суммарные потери напора на сопротивление трению и местные сопротивления находим по формуле полного напора насоса (геометрический напор в этих условиях равен 0):
ч п = H — (p 2 -p 1 ) / (ρ · г) — H г = 7 — ((1-1) · 10 5 ) / (1000 · 9 , 81) — 0 = 7 м
Тогда потери напора на трение составят:
7-0,9125 = 6,0875 м
Рассчитаем значение числа Рейнольдса для потока в трубопроводе (динамическая вязкость воды принята равной 1 · 10 -3 Па · с, а плотность — 1000 кг / м 3 ):
Re = (w · d Э · ρ) / μ = (1,5 · 0,1 · 1000) / (1 · 10 -3 ) = 150000
В соответствии с этим числом с помощью таблицы рассчитываем коэффициент трения (арифметическая формула выбрана из того принципа, что значение Re попадает в диапазон 2,320 λ = 0,316 / Re 0,25 = 0,316 / 150000 0,25 = 0,016 Выразим и найдем максимальную длину трубопровода по формуле потерь на трение напора: l = (H об · d э ) / (λ · [w 2 / (2g)]) = (6,0875 · 0,1) / (0,016 · 0,125) = 304,375 м Дан трубопровод с внутренним диаметром 42 мм. Подключается к водяному насосу с расходом 10 м 3 / час и создающим напором 12 м. Температура перекачиваемой среды 20 ° C. Конфигурация трубопровода представлена на рисунке ниже. Необходимо рассчитать потери напора и проверить, способен ли этот насос перекачивать воду при заданных параметрах трубопровода. Абсолютная шероховатость труб принята равной 0,15 мм. Решение: Рассчитываем скорость потока жидкости в трубопроводе: w = (4 · Q) / (π · d 2 ) = (4 · 10) / (3,14 · 0,042 2 ) · 1/3600 = 2 м / с Напор, соответствующий найденной скорости, будет равен: w 2 / (2 · g) = 2 2 / (2 · 9,81) = 0,204 м Коэффициент трения следует найти до расчета c потерь на трение в трубах.В первую очередь определяем относительную шероховатость трубы: e = Δ / d Э = 0,15 / 42 = 3,57 · 10 -3 мм Критерий Рейнольдса для расхода воды в трубопроводе (динамическая вязкость воды при 20 ° C 1 · 10 -3 Па · с, плотность 998 кг / м 3 ): Re = (w · d Э · ρ) / μ = (2 · 0,042 · 998) / (1 · 10 -3 ) = 83832 Узнаем режим протока воды: 10 / е = 10 / 0,00357 = 2667 560 / е = 560 / 0,00357 = 156863 Найденное значение критерия Рейнольдса находится в диапазоне 2667 <83832 <156,863 (10 / e λ = 0,11 · (e + 68 / Re) 0,25 = 0,11 · (0,00375 + 68/83832) 0,25 = 0,0283 Потери на трение напора в трубопроводе будут равны: H Т = (λ · l) / d э · [w 2 / (2 · g)] = (0,0283 · (15 + 6 + 2 + 1 + 6 + 5)) / 0,042 · 0,204 = 4,8 м Затем необходимо рассчитать потери напора на местные сопротивления.Из схемы трубопровода следует, что местные сопротивления представлены двумя задвижками, четырьмя прямоугольными коленами и одним выходом трубы. Таблицы не содержат значений коэффициента местных сопротивлений для нормальных задвижек и прямоугольных колен с диаметром трубы 42 мм, поэтому воспользуемся одним из способов приблизительного расчета интересующих нас значений. Берем табличные значения коэффициентов местных сопротивлений нормальной задвижки для диаметров 40 и 80 мм.Мы предполагаем, что график значений коэффициентов представляет собой прямую линию в этом диапазоне. Составим и решим систему уравнений, чтобы найти график зависимости коэффициента местного сопротивления от диаметра трубы: { 4,9 = a · 40 + b = { а = -0,0225 Уравнение искомого имеет вид: ζ = -0,0225 · d + 5,8 При диаметре 42 мм коэффициент местного сопротивления будет равен: ζ = -0,0225 · 42 + 5,8 = 4,855 Аналогично находим значение коэффициента местного сопротивления для прямоугольного колена.Мы берем табличные значения для диаметров 37 и 50 мм и решаем систему уравнений, делая аналогичные предположения о характере графика на этом участке: { 1,6 = a · 37 + b = { а = -0,039 Уравнение искомого имеет вид: ζ = -0,039 · d + 3,03 При диаметре 42 мм коэффициент местного сопротивления будет равен: ζ = -0,039 · 42 + 3,03 = 1,392 Для выхода трубы коэффициент местного сопротивления принимается равным единице. Потери напора на местные сопротивления будут равны: ∑ζ МС · [w 2 / (2g)] = (2 · 4,855 + 4 · 1,394 + 1) · 0,204 = 3,3 м Суммарные потери напора в системе будут равны: 4,8 + 3,3 = 8,1 м На основании полученных данных можно сделать вывод, что данный насос подходит для перекачивания воды по этому трубопроводу, так как создаваемый им напор больше, чем общие потери напора в системе, а скорость потока жидкости остается в пределах оптимального запаса. Отрезок прямого горизонтального трубопровода внутренним диаметром 300 мм подвергся ремонту путем замены участка трубопровода длиной 10 м на внутренний диаметр 215 мм. Общая протяженность ремонтируемого участка трубопровода — 50 м. Заменяемый участок находится на расстоянии 18 м от начала. Вода течет по трубопроводу при температуре 20 ° C со скоростью 1,5 м / с. Необходимо выяснить, как изменится гидравлическое сопротивление ремонтируемого участка трубопровода. Коэффициенты трения для труб диаметром 300 и 215 мм принимаются равными 0.01 и 0,012 соответственно. Решение: Первоначальный трубопровод создавал потери напора только из-за трения жидкости о стенки во время откачки. Замена участка трубы привела к появлению двух местных сопротивлений (резкое сжатие и резкое расширение проходного канала) и участка с измененным диаметром трубы, где потери на трение будут другими. Остающийся участок трубопровода не изменился и, следовательно, не может рассматриваться как часть данной проблемы. Рассчитываем расход воды в трубопроводе: Q = (π · d²) / 4 · w = (3,14 · 0,3²) / 4 · 1,5 = 0,106 м³ / с Поскольку расход не меняется по длине трубопровода, можно определить скорость потока на участке трубы, подлежащем ремонту: w = (4 · Q) / (π · d²) = (4 · 0,106) / (3,14 · 0,215²) = 2,92 м / с Полученное значение скорости потока в заменяемом участке трубы находится в оптимальном диапазоне. Для определения коэффициента местного сопротивления сначала рассчитывается критерий Рейнольдса для разных диаметров труб и соотношения площадей поперечного сечения этих труб.Критерий Рейнольдса для трубы диаметром 300 мм (динамическая вязкость воды при 20 ° C 1 · 10 -3 Па · с, а плотность — 998 кг / м 3 ): e = (w · d Э · ρ) / μ = (1,5 · 0,3 · 1000) / (1 · 10 -3 ) = 450000 Критерий Рейнольдса для трубы диаметром 215 мм (динамическая вязкость воды при 20 ° C 1 · 10 -3 Па · с, а плотность — 998 кг / м 3 ): Re = (w · d Э · ρ) / μ = (1,5 · 0,215 · 1000) / (1 · 10 -3 ) = 322500 Соотношение площадей поперечного сечения трубы равно: ((π · d 1 ²) / 4) / ((π · d 2 ²) / 4) = 0,215² / 0,3² = 5,1 По таблицам найдем значения коэффициентов местных сопротивлений, округленные до отношения площадей до 5.Для внезапного расширения он будет равен 0,25, а для внезапного сжатия также будет равен 0,25. Потери напора на местные сопротивления будут равны: ∑ζ МС · [w² / (2g)] = 0,25 · [1,5² / (2 · 9,81)] + 0,25 · [2,92² / (2 · 9,81)] = 0,137 м Теперь рассчитаем потери на трение в замененном участке трубопровода для начального и нового участков трубопровода. Для трубы диаметром 300 мм они будут равны: H Т = (λ · l) / d э · [w² / (2g)] = (0,01 · 10) / 0,3 · [1,5² / (2 · 9,81)] = 0,038 м Для трубы диаметром 215 мм: H Т = (λ · l) / d э · [w² / (2g)] = (0,012 · 10) / 0,215 · 2,92² / (2 · 9,81) = 0,243 м Отсюда делаем вывод, что потери на трение в трубопроводе увеличатся на: 0,243-0,038 = 0,205 м Суммарный прирост потерь на трение в трубопроводе составит: 0,205 + 0,137 = 0,342 м Инженеры всегда готовы оказать консультационные услуги или предоставить дополнительную техническую информацию по предлагаемому нами насосному оборудованию и трубопроводной арматуре. Запросы на трубопроводы просим направлять в технический отдел нашей компании на e-mail: [email protected], телефон +7 (495) 225 57 86 Центральный офис ENCE GmbH Головные представительства в странах СНГ: Россия . После изучения главы 7 бакалавр должен: знаю • обозначение и классификация трубопроводов; • Основы расчета и проектирования трубопроводов; • метод эквивалентной потери напора; • разница между простыми и сложными трубопроводами; • Теория гидроудара в трубах; • влияние кавитации на работу трубопроводов; может • уметь выполнять расчет и проектирование трубопроводов; • построить гидравлические характеристики трубопроводов; • рассчитать гидравлический удар в трубах; собственный • Знания по определению гидроэнергетического баланса насосного агрегата; • математический аппарат для расчета сифонных трубопроводов; • навыки построения суммарных гидравлических характеристик для параллельных и последовательных соединений трубопроводов. Трубопроводы служат для перемещения различных жидкостей и газов. В зависимости от типа перекачиваемой жидкости различают водопроводы, нефтепроводы, нефтепроводы, газопроводы и др. В зависимости от комплектации различают простые и сложные трубопроводы. Простая — это труба, не имеющая ответвлений от точки забора до точки потребления. Комплексные трубопроводы имеют ответвления.Они делятся на следующие основные типы: а) разветвленная или тупиковая; б) трубопроводы с параллельным подключением; в) циркуляр. В зависимости от длины и гидравлических условий расчета они делятся на длинные и короткие. Длинные — те трубопроводы, которые имеют значительную длину и в которых линейные потери напора являются основными. В них местные потери давления обычно специально не учитываются, но принимаются в размере 5-10% от потерь по длине.В коротких трубопроводах основными являются местные потери давления. Расход жидкости в трубопроводе может быть транзитным потоком, т.е. передаваемым по магистрали без выделения, и трековым, т.е. выбранным от магистрали по пути. В самой общей постановке задачи расход Q и положение начальной и конечной точек трубопровода задаются при проектировании трубопроводов.В случае сложного трубопровода задается расход жидкости на всех его участках и расположение потребителей. На основании топографических съемок на плане наносится трасса трубопровода с указанием длины. Определите диаметр трубопровода d и головку H 1 в его начальной точке. Рассматриваемая задача допускает набор решений, поскольку при изменении H 1: чем больше диаметр d , тем меньше требуется напор N 1.Поэтому диаметр трубопровода обычно определяется из экономических расчетов. Очевидно, что с увеличением диаметра трубопровода капитальные затраты будут увеличиваться. Но в то же время снизятся эксплуатационные расходы, так как h2 уменьшается с увеличением d , а затраты энергии на перекачку жидкости уменьшаются. Для определения экономически выгодного диаметра d строится график (рисунок 7.1), на котором кривая S 1 = f 1 (d) — капитальные затраты (руб. ), рассчитанный с учетом срока окупаемости; кривая S2 = f 2 ( d ) ~ эксплуатационные расходы. Рис. 7.1. Схема определения оптимального диаметра трубопровода Тогда общие затраты выражаются кривой, полученной как сумма S = S1 + S2 = f (d). По оси абсцисс и определяется экономически выгодный диаметр, при котором затраты будут наименьшими; S = S мин. Помимо основной рассматриваемой задачи, при расчете трубопроводов могут возникнуть и особые проблемы. 1. Определение перепада напора Δ H = H 1- H 2 при заданном расходе Q и размерах трубопровода. 2. Определение расхода Q для заданного перепада напора Δ H и размеров трубы. 3. Определение диаметра d для заданного расхода Q и разницы напора AN. Если число Рейнольдса мало (коэффициент λ зависит от числа Рейнольдса), то при определении Q или d коэффициент λ = f (Re) становится известным только после расчета завершается, поэтому в этом случае расчет усложняется и проводится методом последовательных приближений. . При проведении расчетов сложных разветвленных многокольцевых гидравлических сетей, питаемых от нескольких источников, использование компьютерных моделей является эффективным направлением, позволяющим практически полностью воспроизводить гидравлические процессы, протекающие в сетях, рассматривая их как единые целые гидравлические системы. Такие модели позволяют определять давление, расход, скорость потока среды, потери напора, энергозатраты на перемещение окружающей среды и т. Д.Решение подобных проблем другими способами для данного типа гидравлической сети в настоящее время невозможно. Основой для построения компьютерной модели является закон Кирхгофа, который используется при расчете электрических сетей. Использование этих законов при расчете гидравлических сетей оправдано полной аналогией протекания тока в проводниках и жидкости в гидросистемах трубопроводов [17]. В качестве конкретного примера мы находим распределение затрат в сети, состоящей из одного кольца с тремя ветвями (рисунок 9.10). Расходы по участкам кольца a , b , c, d обозначим Q a , Q b , Q c, Q д, а по отраслям — через Q 1, Q 2 , Q 3. Требуется найти распределение затрат по разделам а , b , с , d для заданного потока Q на входе в кольцо.Расход воды по ответвлению от кольца Q 1, Q 2 , Q 3 известны, и их сумма равна расходу Q на входе в кольцевую сеть : Q = Q 1 + Q 2 + Q 3. Пример №3

4 = a · 80 + b
б = 5,8
1,1 = a · 50 + b
б = 3,03 Пример № 4

Наша сервисная компания Intekh GmbH
Казахстан
Украина
Туркменистан
Узбекистан
Латвия
Литва ГИДРАВЛИЧЕСКИЙ РАСЧЕТ ТРУБОПРОВОДОВ, Назначение и классификация трубопроводов, Расчет и проектирование трубопроводов
ГИДРАВЛИЧЕСКИЙ РАСЧЕТ ТРУБОПРОВОДОВ
Назначение и классификация трубопроводов
Расчет и проектирование трубопровода
Теоретические основы расчета кольцевых разветвленных гидравлических сетей
Теоретические основы расчета кольцевых разветвленных гидравлических сетей
Рис. 9.10. Схема кольцевой сети
При проведении расчетов принимаем следующие допущения:
1) приток воды в узел будет считаться положительным, а отток из узла — отрицательным;
2) потеря давления для воды, текущей в контуре по часовой стрелке, считается положительной, а против часовой стрелки — отрицательной.
Первый закон Кирхгофа, применяемый к расчету гидравлических систем, устанавливает равенство притока и оттока среды в каждом узле сети, т.е. требуется выполнение уравнения баланса затрат
(9,12)
, где n — количество трубопроводов, соединяемых в узле; — стоимость среды для всех трубопроводов, соединяющихся в данном узле.
Согласно второму закону Кирхгофа сумма напоров для любого замкнутого контура равна нулю:
(9.13)
где — гидравлическое сопротивление сечения и ; — стоимость окружения на участке и .
Используя уравнения (9.12), (9.13), основанные на итерационном методе расчета, можно найти распределение затрат по всем участкам сети при известном расходе Q , заданном на входе в кольцо . На первом этапе итерации произвольное распределение затрат на охрану окружающей среды назначается каждой секции кольца, т.е.е. значения указаны. Тогда для узлов 0, 1, 2 из первого закона Кирхгофа находим
Нет необходимости вводить уравнение Кирхгофа для узла с номером 3, поскольку потребление можно найти, если известны значения затрат для всех других участков сети.
Согласно второму закону Кирхгофа, исходя из принятых затрат для всех участков кольца, находим величину несоответствия давления, т.е.
(9,14)
Если остаточное значение δ H положительное, это означает, что области, в которых направление потока жидкости направлено по часовой стрелке, перегружены, а области, где направление движения противоположное.
Для приближения несоответствия напоров к нулю вводим корректирующий (координатный) поток. Этот расход следует вычесть из расхода на перегруженных участках и прибавить к недогруженным участкам. Величину координационного потока можно найти из соотношения (9.14), положив. Предполагая, что расхождение между головками, полученными по формуле (9.14), положительное, значение связывающего потока находится из соотношения
(9,15)
Если членами, содержащимися, пренебречь, поскольку значения относительно малы, то отношение (9.15) относительно координатной скорости потока будет представлять собой алгебраическое линейное уравнение. Его решение
(9,16)
где — значение всегда положительное. Знаки и всегда должны быть одинаковыми.
После нахождения цены указываются на участках кольца, и заданная последовательность расчетов повторяется заново. Этот итерационный расчет выполняется до тех пор, пока затраты, полученные на последних двух итерациях, не будут отличаться на заданное (довольно маленькое) значение.
Пример. В качестве конкретного примера найдем решение задачи распределения потоков для участков кольцевой сети со следующими исходными данными:
На первом шаге итерационного расчета берем следующие произвольные затраты для участков кольцевой сети:
Применяя формулу (9.14), находим
Величину сцепного течения находим по формуле (9.16):
На втором шаге итерации стоимость участков кольцевой сети составит
Знак расхода
.
Гидравлический расчет трубопровода
Размер встраивания (пикс.)
344 x 292429 x 357514 x 422599 x 487
ОПИСАНИЕ
Описание шаблона Excel для гидравлических расчетов трубопровода
Текст гидравлического расчета трубопровода
- 1. Гидравлический расчет трубопровода Автор: M. Хосравы
2. Пример! Трубопровод состоит из 4 следующих сегментов: Номер сегмента Длина (км) Высота (+ м) Температура (C) 115205022040303501040415 020 3.Вопрос № 1 Если диаметр трубы и входное / выходное давление известны, какова начальная скорость потока природного газа? Внешний диаметр Do 52 дюйма Толщина стенки t 0,25 дюйма Внутренний диаметрDi51,5 дюйма Давление на входе P11152Psi Температура на входе T1 50 CO Давление на входе P2883 Psi Температура на выходе T2 20 ° C 4. Решение: Q (SCF / D) 2,415,957,168 = 68,41 MMSCM / скорость в сутки 27,34 фута / с. Если КПД трубы учитывать 92%, а эффективность — 0,0018. Средняя скорость эрозии составляет 59,2 фута / с, расчетная скорость в порядке.5. Вопрос № 2 Если мы хотим разветвлять и использовать газ вдоль трубопроводов, как показано ниже, каков диаметр трубы костюма в соответствии с желаемым перепадом давления? DistanceFlow Rate Внутренний диаметр Высота Впускной пресс. На выходе Давление.PavNo. (Км) (MMSCM / D) (дюймы) H (+ м) (Psi) (Psi) Psi115 68,4147.9556502 20115211001126.2220 68.4144.3131359 40110010001050.83504044.5039698 101000900 950.841530044.10 расход и давление на входе с диаметром трубы известны для каждого сегмента, как мы можем рассчитать падение давления в каждом сегменте? Внутри InletOutlet Ave.Seg.DistanceFlow RateElevationPavDiameter Press Press. Темп. № (Км) (MMSCM / D) H (+ m) Psi (дюймы). (Psi) (Psi) (C) 1123.34 1 15 68.4147 201152 1094.201 8501063.40 2 20 68.4147 401100 1025.954 730963.284 3 504047 101000 925.6103 140893.891 4 1530470900887.7554 720 7. RPA Thermophysical Module Вычислите AllOf Themophysical вы также можете найти !!! свойства природного газа. 8. Вы можете использовать любую корреляцию коэффициента трения в RPA! 0.9 16167 k 37530 A2 2.457. ln 0,27.A3 Re D Re 1k = Шероховатость в футах 1212 81 f 8.D = внутренний диаметр в футах Re 3 2A2A3Re = число Рейнольдса 1,1098k 0,8981D 7,149 A42.8257Re 21,4 f k = Шероховатость в футах k D5.0452. D = внутренний диаметр в футах 4. loglog A 4 3.7065 Re Re = число Рейнольдса 9. Спасибо за внимание
.
