Как найти объем комнаты: Как найти объем помещения. Как рассчитать, посчитать объем помещения
Как найти объем помещения. Как рассчитать, посчитать объем помещения
Как рассчитать, посчитать объем помещения.
Оценка объема помещений довольно часто требуется при производстве строительных и ремонтных работ. В большинстве случаев это требуется для уточнения количества материалов, необходимых для проведения ремонта, а также для подбора эффективной системы отопления или кондиционирования воздуха. Количественные характеристики, описывающие пространство, как правило, требуют проведения некоторых измерений и несложных вычислений.
1. Самый простой случай – когда требуется определить объем помещения правильной прямоугольной или квадратной формы. При помощи рулетки измерьте в метрах длину и ширину стен, а также высоту помещения. Удобнее всего проводить измерения по полу, вдоль плинтусов. Перемножьте полученные показатели длинны, ширины, высоты и вы получите искомый объем.
2. Если помещение имеет неправильную или сложную форму, задача немного усложняется. Разбейте площадь помещения на несколько простых фигур (прямоугольников, квадратов, полуокружностей и так далее) и вычислите площадь каждой из них, предварительно произведя замеры. Сложите полученные значения, суммируя площадь. Умножьте сумму на высоту помещения. Измерения необходимо проводить в одних и тех же единицах, например, в метрах.
Разбейте площадь помещения на несколько простых фигур (прямоугольников, квадратов, полуокружностей и так далее) и вычислите площадь каждой из них, предварительно произведя замеры. Сложите полученные значения, суммируя площадь. Умножьте сумму на высоту помещения. Измерения необходимо проводить в одних и тех же единицах, например, в метрах.
3. При проведении строительных работ определение объема всего сооружения определяется по стандартам. Так называемый строительный объем наземной части здания с чердаком можно вычислить, умножив площадь горизонтального сечения по внешним обводам на уровне нижнего этажа. Измерьте полную высоту здания от уровня чистого пола до верхней части утеплителя чердачного перекрытия. Перемножьте оба показателя.
4. При наличии разных по площади этажей общий объем помещений в здании определите, сложив объемы всех частей. Таким же образом определяется объем, если помещения имеют разные очертания и конструкцию.
5. Отдельно вычислите объемы веранд, эркеров, тамбуров и иных вспомогательных элементов сооружения (за исключением крытых и открытых балконов). Включите эти данные в общий объем всех помещений здания. Таким образом можно легко найти объем любого помещения или здания, расчеты довольно просты, пробуйте и будьте внимательны.
Включите эти данные в общий объем всех помещений здания. Таким образом можно легко найти объем любого помещения или здания, расчеты довольно просты, пробуйте и будьте внимательны.
Формула объема помещения
Формула
Пример расчета объема помещения по формуле
Калькулятор площади стены или пола
Вставьте размеры помещения и получите результат.
Как посчитать площадь комнаты, стены, пола, потолка
Периодически нам требуется знать площадь и объем комнаты. Эти данные могут понадобиться при проектировании отопления и вентиляции, при закупке стройматериалов и еще во многих других ситуациях. Также периодически требуется знать площадь стен. Все эти данные вычисляются легко, но предварительно придется поработать рулеткой — измерять все требуемые габариты. О том, как посчитать площадь комнаты и стен, объем помещения и пойдет речь дальше.
Часто требуется посчитать кубатуру комнаты, ее объем
Содержание статьи
Площадь комнаты в квадратных метрах
Посчитать несложно, требуется только вспомнить простейшие формулы а также провести измерения. Для этого нужны будут:
Для этого нужны будут:
- Рулетка. Лучше — с фиксатором, но подойдет и обычная.
- Бумага и карандаш или ручка.
- Калькулятор (или считайте в столбик или в уме).
Набор инструментов нехитрый, найдется в каждом хозяйстве. Проще измерения проводить с помощником, но можно справиться и самостоятельно.
Для начала надо измерить длину стен. Делать это желательно вдоль стен, но если все они заставлены тяжелой мебелью, можно проводить измерения и посередине. Только в этом случае следите чтобы лента рулетки лежала вдоль стен, а не наискосок — погрешность измерений будет меньше.
Прямоугольная комната
Если помещение правильной формы, без выступающих частей, вычислить площадь комнаты просто. Измеряете длину и ширину, записываете на бумажке. Цифры пишите в метрах, после запятой ставите сантиметры. Например, длина 4,35 м (430 см), ширина 3,25 м (325 см).
Как высчитать площадь комнаты
Найденные цифры перемножаем, получаем площадь комнаты в квадратных метрах. Если обратимся к нашему примеру, то получится следующее: 4,35 м * 3,25 м = 14,1375 кв. м. В данной величине оставляют обычно две цифры после запятой, значит округляем. Итого, рассчитанная квадратура комнаты 14,14 квадратных метров.
Если обратимся к нашему примеру, то получится следующее: 4,35 м * 3,25 м = 14,1375 кв. м. В данной величине оставляют обычно две цифры после запятой, значит округляем. Итого, рассчитанная квадратура комнаты 14,14 квадратных метров.
Помещение неправильной формы
Если надо высчитать площадь комнаты неправильной формы, ее разбивают на простые фигуры — квадраты, прямоугольники, треугольники. Потом измеряют все нужные размеры, производят расчеты по известным формулам (есть в таблице чуть ниже).
Перед тем как посчитать площадь комнаты, тоже проводим изменения. Только в этом случае цифр будет не две, а четыре: добавится еще длина и ширина выступа. Габариты обоих кусков считаются отдельно.
Один из примеров — на фото. Так как и то, и другое — прямоугольник, площадь считается по той же формуле: длину умножаем на ширину. Найденную цифру надо отнять или прибавить к размеру помещения — в зависимости от конфигурации.
Площадь комнаты сложной формы
Покажем на этом примере как посчитать площадь комнаты с выступом (изображена на фото выше):
- Считаем квадратуру без выступа: 3,6 м * 8,5 м = 30,6 кв.
 м.
м. - Считаем габариты выступающей части: 3,25 м * 0,8 м = 2,6 кв. м.
- Складываем две величины: 30,6 кв. м. + 2,6 кв. м. = 33,2 кв. м.
Еще бывают помещения со скошенными стенами. В этом случае разбиваем ее так, чтобы получились прямоугольники и треугольник (как на рисунке ниже). Как видите, для данного случая требуется иметь пять размеров. Разбить можно было по-другому, поставив вертикальную, а не горизонтальную черту. Это не важно. Просто требуется набор простых фигур, а способ их выделения произвольный.
Как посчитать площадь комнаты неправильной формы
В этом случае порядок вычислений такой:
- Считаем большую прямоугольную часть: 6,4 м * 1,4 м = 8,96 кв. м. Если округлить, получим 9, 0 кв.м.
- Высчитываем малый прямоугольник: 2,7 м * 1,9 м = 5,13 кв. м. Округляем, получаем 5,1 кв. м.
- Считаем площадь треугольника. Так как он с прямым углом, то равен половине площади прямоугольника с такими же размерами. (1,3 м * 1,9 м) / 2 = 1,235 кв.
 м. После округления получаем 1,2 кв. м.
м. После округления получаем 1,2 кв. м. - Теперь все складываем чтобы найти общую площадь комнаты: 9,0 + 5,1 + 1,2 = 15,3 кв. м.
Планировка помещений может быть очень разнообразной, но общий принцип вы поняли: делим на простые фигуры, измеряем все требуемые размеры, высчитываем квадратуру каждого фрагмента, потом все складываем.
Формулы расчета площади и периметра простых геометрических фигур
Еще одно важное замечание: площадь комнаты, пола и потолка — это все одинаковые величины. Отличия могут быть если есть какие-то полу-колоны, не доходящие до потолка. Тогда из общей квадратуры вычитается квадратура этих элементов. В результате получаем площадь пола.
Как рассчитать квадратуру стен
Определение площади стен часто требуется при закупке отделочных материалов — обоев, штукатурки и т.п. Для этого расчета нужны дополнительные измерения. К имеющимся уже ширине и длине комнаты нужны будут:
- высота потолков;
- высота и ширина дверных проемов;
- высота и ширина оконных проемов.

Все измерения — в метрах, так как квадратуру стен тоже принято измерять в квадратных метрах.
Удобнее всего размеры наносить на план
Так как стены прямоугольные, то и площадь считается как для прямоугольника: длину умножаем на ширину. Таким же образом вычисляем размеры окон и дверных проемов, их габариты вычитаем. Для примера рассчитаем площадь стен, изображенных на схеме выше.
- Стена с дверью:
- 2,5 м * 5,6 м = 14 кв. м. — общая площадь длинной стены
- сколько занимает дверной проем: 2,1 м *0,9 м = 1,89 кв.м.
- стена без учета дверного проема — 14 кв.м — 1,89 кв. м = 12,11 кв. м
- Стена с окном:
- квадратура маленьких стен: 2,5 м * 3,2 м = 8 кв.м.
- сколько занимает окно: 1,3 м * 1,42 м = 1,846 кв. м, округляем, получаем 1,85 кв.м.
- стена без оконного проема: 8 кв. м — 1,75 кв.м = 6,25 кв.м.
Найти общую площадь стен не составит труда. Складываем все четыре цифры: 14 кв.м + 12,11 кв. м. + 8 кв.м + 6,25 кв.м. = 40,36 кв. м.
м. + 8 кв.м + 6,25 кв.м. = 40,36 кв. м.
Объем комнаты
Формула расчета объема комнаты
Для некоторых расчетов требуется объем комнаты. В этом случае перемножаются три величины: ширина, длинна и высота помещения. Измеряется данная величина в кубических метрах (кубометрах), называется еще кубатурой. Для примера используем данные из предыдущего пункта:
- длинна — 5,6 м;
- ширина — 3,2 м;
- высота — 2,5 м.
Если все перемножить, получаем: 5,6 м * 3,2 м * 2,5 м = 44,8 м3. Итак, объем помещения 44,8 куба.
Как найти объем помещения. Как рассчитать, посчитать объем помещенияКак рассчитать, посчитать объем помещения. Оценка объема помещений довольно часто требуется при производстве строительных и ремонтных работ. В большинстве случаев это требуется для уточнения количества материалов, необходимых для проведения ремонта, а также для подбора эффективной системы отопления или кондиционирования воздуха. 1. Самый простой случай – когда требуется определить объем помещения правильной прямоугольной или квадратной формы. При помощи рулетки измерьте в метрах длину и ширину стен, а также высоту помещения. Удобнее всего проводить измерения по полу, вдоль плинтусов. Перемножьте полученные показатели длинны, ширины, высоты и вы получите искомый объем. 2. Если помещение имеет неправильную или сложную форму, задача немного усложняется. Разбейте площадь помещения на несколько простых фигур (прямоугольников, квадратов, полуокружностей и так далее) и вычислите площадь каждой из них, предварительно произведя замеры. Сложите полученные значения, суммируя площадь. Умножьте сумму на высоту помещения. Измерения необходимо проводить в одних и тех же единицах, например, в метрах. 3. При проведении строительных работ определение объема всего сооружения определяется по стандартам. 4. При наличии разных по площади этажей общий объем помещений в здании определите, сложив объемы всех частей. Таким же образом определяется объем, если помещения имеют разные очертания и конструкцию. 5. Отдельно вычислите объемы веранд, эркеров, тамбуров и иных вспомогательных элементов сооружения (за исключением крытых и открытых балконов). Включите эти данные в общий объем всех помещений здания. Таким образом можно легко найти объем любого помещения или здания, расчеты довольно просты, пробуйте и будьте внимательны. Формула объема помещенияФормула Пример расчета объема помещения по формуле Калькулятор площади стены или полаВставьте размеры помещения и получите результат. sdelalremont.ru Как найти объем помещения |Как рассчитать, посчитать объем помещения. Оценка объема помещений довольно часто требуется при производстве строительных и ремонтных работ. В большинстве случаев это требуется для уточнения количества материалов, необходимых для проведения ремонта, а также для подбора эффективной системы отопления или кондиционирования воздуха. Количественные характеристики, описывающие пространство, как правило, требуют проведения некоторых измерений и несложных вычислений. 1. Самый простой случай – когда требуется определить объем помещения правильной прямоугольной или квадратной формы. При помощи рулетки измерьте в метрах длину и ширину стен, а также высоту помещения. Удобнее всего проводить измерения по полу, вдоль плинтусов. Перемножьте полученные показатели длинны, ширины, высоты и вы получите искомый объем. 2. Если помещение имеет неправильную или сложную форму, задача немного усложняется. Разбейте площадь помещения на несколько простых фигур (прямоугольников, квадратов, полуокружностей и так далее) и вычислите площадь каждой из них, предварительно произведя замеры. 3. При проведении строительных работ определение объема всего сооружения определяется по стандартам. Так называемый строительный объем наземной части здания с чердаком можно вычислить, умножив площадь горизонтального сечения по внешним обводам на уровне нижнего этажа. Измерьте полную высоту здания от уровня чистого пола до верхней части утеплителя чердачного перекрытия. Перемножьте оба показателя. 4. При наличии разных по площади этажей общий объем помещений в здании определите, сложив объемы всех частей. Таким же образом определяется объем, если помещения имеют разные очертания и конструкцию. 5. Отдельно вычислите объемы веранд, эркеров, тамбуров и иных вспомогательных элементов сооружения (за исключением крытых и открытых балконов). Включите эти данные в общий объем всех помещений здания. Таким образом можно легко найти объем любого помещения или здания, расчеты довольно просты, пробуйте и будьте внимательны. Формула объема помещенияФормула Пример расчета объема помещения по формуле. Источник: http://sdelalremont.ru Метки: Cтроительство домов, дачные дома, деревянные дома, дом из бруса, дома из бруса, евроремонт, загородная недвижимость, загородные дома, земляные работы, как построить дом, котеджи, коттедж, прайс лист строительных работ, продажа готовых проектов, продажа котеджей, продажа коттеджей, проект деревянного дома, проект загородного дома, проект кирпичного дома, проектирование домов, проектирование коттеджей, проекты деревянных домов, проекты домов, проекты загородных коттеджей, проекты кирпичных домов, проекты котеджей, проекты коттеджей, ремонт Киев, ремонт Киевская область, ремонт офисов, ремонт под ключ, снос зданий, строительные компании, строительные компании Киев, строительство в Киеве, строительство дач, строительство дачных домов, строительство деревянного дома, строительство деревянных домов, строительство дома, строительство дома из бруса, строительство загородного дома, строительство загородных домов, строительство катеджей, строительство кирпичных домов, строительство котеджей, строительство коттеджей, стройгрупп, таунхаус, участок с домом, шпунтовое ограждение remontnew. Как найти объем помещения — каталог статей на сайте — ДомСтройПри организации вентиляции, кондиционирования, вытяжки и во многих других случаях нужно найти объем помещения. Именно от объема помещения будет зависеть необходимая мощность аппаратуры, которую потребуется установить. Объем помещения измеряется в «кубах», то есть в кубических сантиметрах и кубических метрах. Конечно же, принято все переводить в кубические метры. Другими словами, 50 кубических сантиметров, записывается как 0,5 кубических метров. Объем помещения находят по простейшей формуле, которая должна быть знакома каждому еще со школьной скамьи. Нужно узнать линейные размеры данного помещения в трех измерениях и перемножить их между собой. То есть для начала берут длинную линейку, метр или рулетку и измеряют высоту помещения, длину помещения и его ширину. Эти значения надо записывать на бумагу, чтобы не забыть. Когда размеры будут известны, их умножают друг на друга. В итоге получают искомую цифру в кубических метрах, которая выражает в количественных характеристиках объем помещения. Можно воспользоваться и другим методом. Найти площадь пола (а возможно, что она уже и так известна), а затем умножить ее на высоту потолка. Результат будет тем же, что и расчеты по предыдущей формуле. Что делать, если помещение имеет не совсем стандартную форму? К примеру, помещение может состоять из нескольких «кубиков». В таком случае его следует разбить на более удобные для расчетов участки. После этого находят объем каждого из этих участков по отдельности. А когда это будет выполнено, итоги расчетов складывают. Разумеется, лучше округлять найденные значения объема в большую сторону. ПО ТЕМЕ: Как найти площадь стен, потолка и пола: стандарт и нестандарт Tags: ламинат обои перепланировка www.domstoy.ru Как измерить и посчитать объем комнаты, вычислить кубатуру расходных материалов?В данной теме мы рассмотрим, как вычислить объем любого помещения. Если вы затеяли ремонт или просто хотите немного освежить вашу квартиру или дом, но не знаете, как измерить объем комнаты, то эта статья для вас. Как измерить объем комнаты и рассчитать квадратуру для расходных материалов?Кстати, не всегда объем комнаты нужен только для переклейки обоев или новой покраски помещения. При установке радиаторов, кондиционеров или спит-систем также необходимо знать данные габариты. Начнем же мы с общего понятия, что такое объем, а также проанализируем, для чего при ремонте его нужно обязательно знать. Важно: По таким формулам вы сможете рассчитывать не только размеры самой комнаты, но и кубатуру затратных материалов для ремонта. Например, чтобы просчитать песок или цемент для стяжки. Но в таком случае вам потребуется знать будущую высоту полагаемого покрытия. Для любых ремонтных работ и для каждой комнаты необходимы расчеты площади и объема помещения Объем – это термин, необходимый для измерения высоты, длины и ширины сосуда или другого пространства. Поэтому и высчитать объем можно, зная высоту, длину и ширину измеряемого пространства, а также его форму.
Это самая простая формула, что пригодится каждому жильцу для ремонта Как измерить объем комнаты, которая имеет правильные размеры?
Важно: Если у вас действительно равносторонняя комната, тогда нужно просто возвести в квадрат один размер, умножив на высоту помещения. А если у вас и последний габарит равносторонний, то для кубической комнаты один размер возводите в куб. Но это лишь познавательная теория. На практически подобные помещения кране редко встречаются.
При замерах рулетку нужно держать максимально ровно
Важно помнить, что все результаты, которые вы узнали, нужно считать в одних единицах. Это могут быть метры или сантиметры, если пространство совсем маленькое и т.д. Но если вы делаете все по правилам, то единица измерения в данном случае – метр кубический. Как видите, ничего сложного нет Как посчитать объем комнаты, которая имеет неправильную форму?
Ваши действия, если комната имеет закругления Как вычислить объем комнаты, если она имеет еще и сложную форму?Порой помещения имею различные арки или ниши неправильной формы, а точнее – в виде круга или треугольника. Большая часть из нас вряд ли вспомнит формулы по геометрии, тем более нюансов в этой сфере хоть отбавляй. Например, у вас в комнате есть выступ, что идет полукругом
При сложной конструкции, просто разбивайте комнату на несколько простых участков Но ведь бывают и треугольные углубления или части комнаты
Как видите, нет ничего сложного в расчете или измерении объема комнаты. Важно просто делать правильно все замеры и вооружиться запасом некоторых школьных формул, базовые из которых мы вам предоставили. И не забывайте, что при ремонте не помешает делать небольшие наброски в лишних материалах. Видео: Как вычислить объем комнаты и кубатуру?Оцените статью heaclub.ru |
Объем комнаты и площадь пола
Вот такая вот интересная задачка:
Объем комнаты 75 метров кубических, высота комнаты 3 метра. Найдите площадь пола.
Решение задачи тупо:
75 : 3 = 25 (метров квадратных)
Если объем комнаты разделить на её высоту, то получится площадь пола. Если в вашей задаче написано «объем комнаты 75 метров квадратных…», то значит эту задачу составляло туловище, которое ни фига не понимает в единицах измерения объемов. Объем не может измеряться в метрах квадратных, нормальные люди в них измеряют площадь.
А теперь бла-бла-бла на заданную тему.
Ничего сложного в этой задаче нет, просто вместо обычного прямоугольного параллелепипеда здесь нам рассказывают о комнате. В переводе на язык математики и применительно к параллелепипеду эта задача будет звучать так:
Объем прямоугольного параллелепипеда равен 75 кубических метров, его высота равна 3 метра. Найдите площадь основания этого прямоугольного параллелепипеда.
В чём маленький подвох, который многих может сбить с толку? Дело в том, что комнату мы привыкли видеть изнутри.
| Высота комнаты и площадь пола |
Эта комната изображена на стадии ремонта. После ремонта можете обставить её мебелью по своему вкусу. Кстати, большинство людей вспоминают про геометрию именно после начала ремонта — площади, периметры, объемы… Так вот, математики нам показывают прямоугольные параллелепипеды всегда снаружи.
| Прямоугольный параллелепипед с обозначениями |
Если в математике мы привыкли видеть любой объем снаружи, то попадая внутрь реального объема очень легко растеряться.
Теперь разберемся с названиями. То, что в комнате называется «объем комнаты», в математике называется просто «объем». «Высота комнаты» в математике будет просто «высота», а «площадь пола» — это ничто иное, как «площадь основания». Хорошо или плохо, но математики нас учат, что если площадь основания умножить на высоту, то мы получим объем. При решении задачи мы объем разделили на высоту и получили площадь.
Еще один интересный момент. Комната может иметь любую форму с вертикальными стенами. Пол в комнате может быть квадратным, прямоугольным, треугольным, шестиугольным, круглым, бесформенным… В любом случае, его площадь будет равна 25 квадратных метров. Ведь любая двухмерная геометрическая фигура может иметь площадь в 25 метров в квадрате. При умножении этой площади на высоту в 3 метра мы всегда будем получать объем в 75 метров кубических.
Является ли подобная задача реальной? Волне. В отдельных бюрократических документах можно встреть объем комнаты. Например, при установке газового оборудования требования могут предъявляться не к площади комнаты, а к её объему.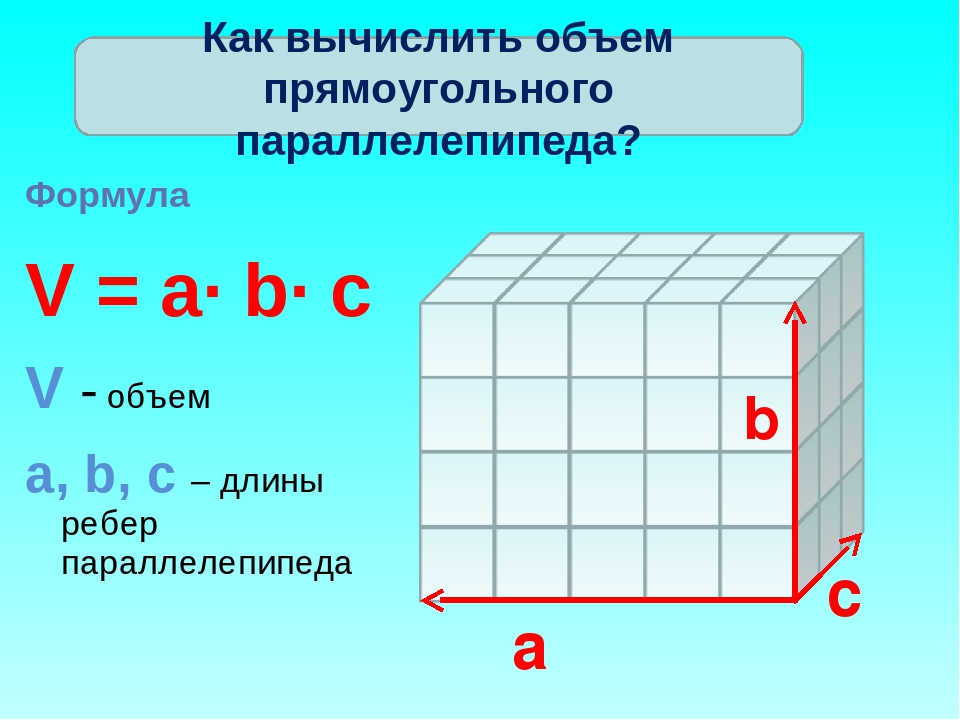 Исходя из высоты комнаты, которая может быть разной в разных зданиях, определяют требуемую площадь пола для соблюдения строительных норм. Фокус в том, что в горении принимает участие газ кислород и его должно быть необходимое количество. Нужный объем кислорода может находиться как в маленькой и высокой комнате, так и в большой, но низкой. Разные числа при умножении могут давать один и тот же результат.
Исходя из высоты комнаты, которая может быть разной в разных зданиях, определяют требуемую площадь пола для соблюдения строительных норм. Фокус в том, что в горении принимает участие газ кислород и его должно быть необходимое количество. Нужный объем кислорода может находиться как в маленькой и высокой комнате, так и в большой, но низкой. Разные числа при умножении могут давать один и тот же результат.
P.S. Кстати, на сайте «Русский текст» вы можете найти редкие и уникальные тексты, статьи из старых газет, интересные публикации на русском языке. Любознательность ещё никому не навредила. Конечно, если любознательностью попользоваться с умом. Если вы прочтете какую-нибудь старую, давно забытую, но интересную статью о науке — вы станете умнее, чем были до этого.
Калькулятор расчёта площади комнаты, расчет площади пола и потолка
Приведу пример расчета пола или потолка комнаты (кухни) в квадратных метрах.
Формула расчета простая, S = a*b, где S — площадь, а и b — соответственно, длина и ширина комнаты.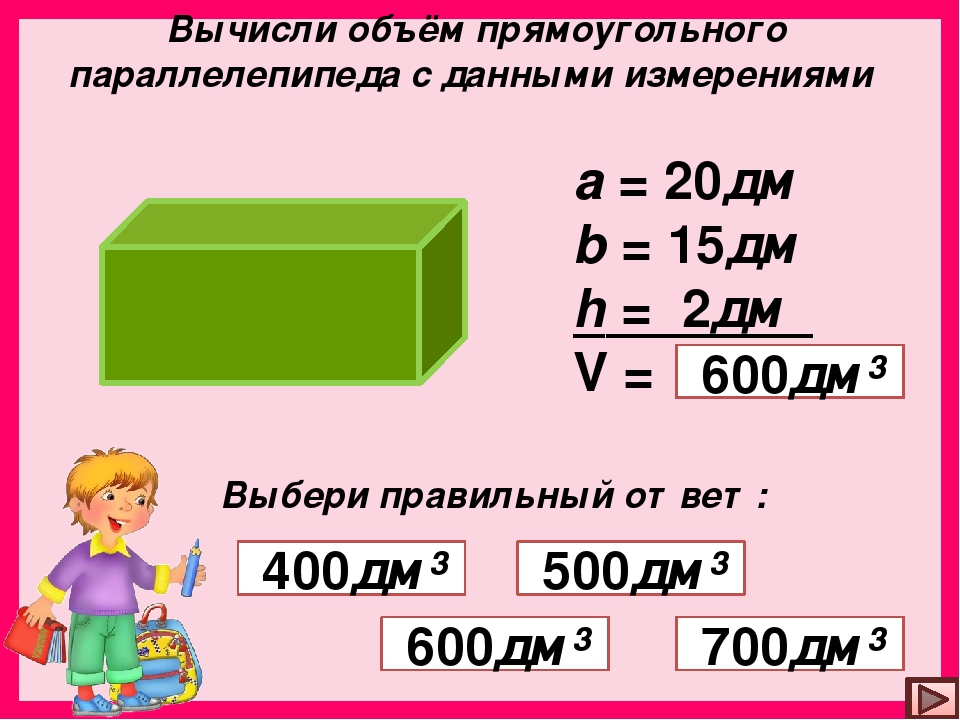
В нашем примере (рисунка с обмерами) вместо маленьких букв длина — А и ширина — Б., и противоположенных стен — Г и В.
Чтобы рассчитать площадь комнаты по полу:
— если у нас длина комнаты 5 метра, а ширина 3 метров, тогда нам надо ( 5*3 = 15 кв.м.), в итоге получаем 15 кв.м. по полу
Воспользуйтесь нашим Калькулятором, чтобы расчитать площадь пола или потолка
Если вы не хотите в ручную рассчитывать площадь пола или вы, что то не поняли при описание расчетов, то вы можете воспользоваться нашим калькулятором и рассчитать площадь пола или потолка автоматически.
Для расчёта необходимо измерить в метрах длину, ширину комнаты и внести данные по порядку заполнив форму и вы автоматически получите расчет площади пола или потолка в квадратных метрах.
Калькулятор расчёта площади пола
Примечание:
Обращаем ваше внимание, что измерения необходимо проводить в метрах. Т.е. если вы получили длину комнаты 964 сантиметров, то в поля формы необходимо ввести значение 9.64. Обратите внимание, что дробные числа нужно вводить с точкой, а не с запятой!
Т.е. 2,6 — неправильно, 2.6 — правильно
Калькулятор рассчитывает не только площадь пола или потолка, данный калькулятор можно также использовать для расчёта площади любых других прямоугольных объектов у которых есть длина и ширина. В этом случае вместо ширины и длины комнаты вам необходимо подставить значения ширины и длины этих самых объектов (окна, двери и т.д.,) к примеру таких как площадь окон и дверей.
К примеру как можно проверить и расчитать в ручную площадь окон и дверей. :
:
— если у нас размеры окна ширина 1,6 метров, а высота 1,5 метров.
— а двери ширина 0,8 метров, а высота 2,05 метров.
Окно: (1,6*1,5)= 2,4 кв.м., в итоге окно получаем 2,4 кв.м.,
Двери: (0,8*2,05)= 1,64 кв.м, в итоге двери получаем 1,64 кв.м.,
Чтобы рассчитать площадь комнаты по стенам: воспользуйтесь нашим Калькулятором, чтобы расчитать площадь стен
Источник: remont-otdelka-m.ru
Периметр, площадь и объем
Данный материал содержит геометрические фигуры с измерениями. Приведённые измерения являются приблизительными и могут не совпадать с измерениями в реальной жизни.
Периметр геометрической фигуры
Периметр геометрической фигуры — это сумма всех её сторон. Чтобы вычислить периметр, нужно измерить каждую сторону и сложить результаты измерений.
Вычислим периметр следующей фигуры:
Это прямоугольник. Детальнее мы поговорим об этой фигуре позже. Сейчас просто вычислим периметр этого прямоугольника. Длина его равна 9 см, а ширина 4 см.
Детальнее мы поговорим об этой фигуре позже. Сейчас просто вычислим периметр этого прямоугольника. Длина его равна 9 см, а ширина 4 см.
У прямоугольника противоположные стороны равны. Это видно на рисунке. Если длина равна 9 см, а ширина равна 4 см, то противоположные стороны будут равны 9 см и 4 см соответственно:
Найдём периметр. Для этого сложим все стороны. Складывать их можно в любом порядке, поскольку от перестановки мест слагаемых сумма не меняется. Периметр часто обозначается заглавной латинской буквой P (англ. perimeters). Тогда получим:
P = 9 см + 4 см + 9 см + 4 см = 26 см.
Поскольку у прямоугольника противоположные стороны равны, нахождение периметра записывают короче — складывают длину и ширину, и умножают её на 2, что будет означать «повторить длину и ширину два раза»
P = 2 × (9 + 4) = 18 + 8 = 26 см.
Квадрат это тот же прямоугольник, но у которого все стороны равны. Например, найдём периметр квадрата со стороной 5 см. Фразу «со стороной 5 см» нужно понимать как «длина каждой стороны квадрата равна 5 см»
Фразу «со стороной 5 см» нужно понимать как «длина каждой стороны квадрата равна 5 см»
Чтобы вычислить периметр, сложим все стороны:
P = 5 см + 5 см + 5 см + 5 см = 20 см
Но поскольку все стороны равны, вычисление периметра можно записать в виде произведения. Сторона квадрата равна 5 см, и таких сторон 4. Тогда эту сторону, равную 5 см нужно повторить 4 раза
P = 5 см × 4 = 20 см
Площадь геометрической фигуры
Площадь геометрической фигуры — это число, которое характеризует размер данной фигуры.
Следует уточнить, что речь в данном случае идёт о площади на плоскости. Плоскостью в геометрии называют любую плоскую поверхность, например: лист бумаги, земельный участок, поверхность стола.
Площадь измеряется в квадратных единицах. Под квадратными единицами подразумевают квадраты, стороны которых равны единице. Например, 1 квадратный сантиметр, 1 квадратный метр или 1 квадратный километр.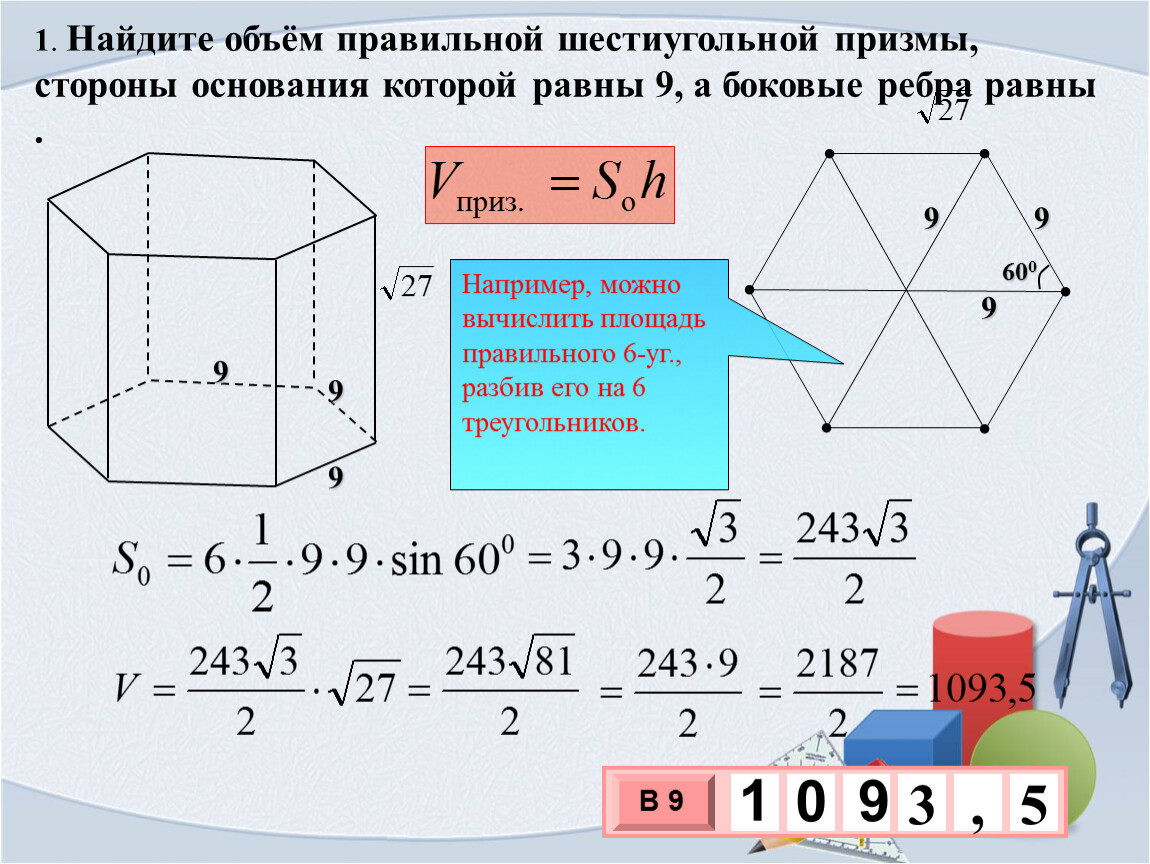
Измерить площадь какой-нибудь фигуры означает выяснить сколько квадратных единиц содержится в данной фигуре.
Например, площадь следующего прямоугольника равна трём квадратным сантиметрам:
Это потому что в данном прямоугольнике содержится три квадрата, каждый из которых имеет сторону, равную одному сантиметру:
Справа представлен квадрат со стороной 1 см (он в данном случае является квадратной единицей). Если посмотреть сколько раз этот квадрат входит в прямоугольник, представленный слева, то обнаружим, что он входит в него три раза.
Следующий прямоугольник имеет площадь, равную шести квадратным сантиметрам:
Это потому что в данном прямоугольнике содержится шесть квадратов, каждый из которых имеет сторону, равную одному сантиметру:
Допустим, потребовалось измерить площадь следующей комнаты:
Определимся в каких квадратах будем измерять площадь. В данном случае площадь удобно измерить в квадратных метрах:
Итак, наша задача состоит в том, чтобы определить сколько таких квадратов со стороной 1 м содержится в исходной комнате. Заполним этим квадратом всю комнату:
Заполним этим квадратом всю комнату:
Видим, что квадратный метр содержится в комнате 12 раз. Значит, площадь комнаты составляет 12 квадратных метров.
Площадь прямоугольника
В предыдущем примере мы вычислили площадь комнаты, последовательно проверив сколько раз в ней содержится квадрат, сторона которого равна одному метру. Площадь составила 12 квадратных метров.
Комната представляла собой прямоугольник. Площадь прямоугольника можно вычислить перемножив его длину и ширину.
Чтобы вычислить площадь прямоугольника, нужно перемножить его длину и ширину.
Вернёмся к предыдущему примеру. Допустим, мы измерили длину комнаты рулеткой и оказалось, что длина составила 4 метра:
Теперь измерим ширину. Пусть она составила 3 метра:
Умножим длину (4 м) на ширину (3 м).
4 × 3 = 12
Как и в прошлый раз получаем двенадцать квадратных метров. Это объясняется тем, что измерив длину, мы тем самым узнаём сколько раз можно уложить в эту длину квадрат со стороной, равной одному метру. Уложим четыре квадрата в эту длину:
Уложим четыре квадрата в эту длину:
Затем мы определяем сколько раз можно повторить эту длину с уложенными квадратами. Это мы узнаём, измерив ширину прямоугольника:
Площадь квадрата
Квадрат это тот же прямоугольник, но у которого все стороны равны. Например, на следующем рисунке представлен квадрат со стороной 3 см. Фраза «квадрат со стороной 3 см» означает, что все стороны равны 3 см
Площадь квадрата вычисляется таким же образом, как и площадь прямоугольника — длину умножают на ширину.
Вычислим площадь квадрата со стороной 3 см. Умножим длину 3 см на ширину 3 см
3 × 3 = 9
В данном случае требовалось узнать сколько квадратов со стороной 1 см содержится в исходном квадрате. В исходном квадрате содержится девять квадратов со стороной 1 см. Действительно, так оно и есть. Квадрат со стороной 1 см, входит в исходный квадрат девять раз:
Умножив длину на ширину, мы получили выражение 3 × 3, а это есть произведение двух одинаковых множителей, каждый из которых равен 3. Иными словами выражение 3 × 3 представляет собой вторую степень числа 3. А значит процесс вычисления площади квадрата можно записать в виде степени 32.
Иными словами выражение 3 × 3 представляет собой вторую степень числа 3. А значит процесс вычисления площади квадрата можно записать в виде степени 32.
Поэтому вторую степень числа называют квадратом числа. При вычислении второй степени числа a, человек тем самым находит площадь квадрата со стороной a. Операцию возведения числа во вторую степень по другому называют возведением в квадрат.
Обозначения
Площадь обозначается заглавной латинской буквой S (англ. Square — квадрат). Тогда площадь квадрата со стороной a см будет вычисляться по следующему правилу
S = a2
где a — длина стороны квадрата. Вторая степень указывает на то, что происходит перемножение двух одинаковых сомножителей, а именно длины и ширины. Ранее было сказано, что у квадрата все стороны равны, а значит равны длина и ширина квадрата, выраженные через букву a.
Если задача состоит в том, чтобы определить сколько квадратов стороной 1 см содержится в исходном квадрате, то в качестве единиц измерения площади нужно указывать см2. Это обозначение заменяет словосочетание «квадратный сантиметр».
Например, вычислим площадь квадрат со стороной 2 см.
Значит, квадрат со стороной 2 см, имеет площадь, равную четырём квадратным сантиметрам:
Если задача состоит в том, чтобы определить сколько квадратов со стороной 1 м содержится в исходном квадрате, то в качестве единиц измерения нужно указывать м2. Это обозначение заменяет словосочетание «квадратный метр».
Вычислим площадь квадрата со стороной 3 метра
Значит, квадрат со стороной 3 м, имеет площадь равную девяти квадратным метрам:
Аналогичные обозначения используются при вычислении площади прямоугольника. Но длина и ширина прямоугольника могут быть разными, поэтому они обозначаются через разные буквы, например a и b.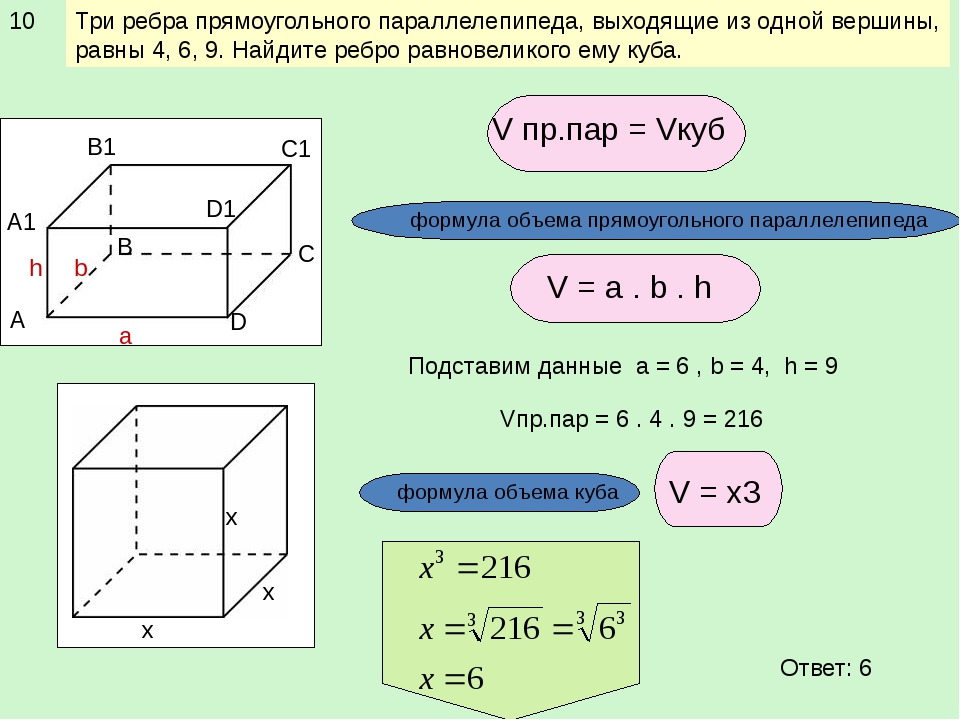 Тогда площадь прямоугольника, длиной a и шириной b вычисляется по следующему правилу:
Тогда площадь прямоугольника, длиной a и шириной b вычисляется по следующему правилу:
S = a × b
Как и в случае с квадратом, единицами измерения площади прямоугольника могут быть см2, м2, км2. Эти обозначения заменяют словосочетания «квадратный сантиметр», «квадратный метр», «квадратный километр» соответственно.
Например, вычислим площадь прямоугольника, длиной 6 см и шириной 3 см
Значит, прямоугольник длиной 6 см и шириной 3 см имеет площадь, равную восемнадцати квадратным сантиметрам:
В качестве единицы измерения допускается использовать словосочетание «квадратных единиц». Например, запись S = 3 кв.ед означает, что площадь квадрата или прямоугольника равна трём квадратам, каждый из которых имеет единичную сторону (1 см, 1 м или 1 км).
Перевод единиц измерения площади
Единицы измерения площади можно переводить из одной единицы измерения в другую.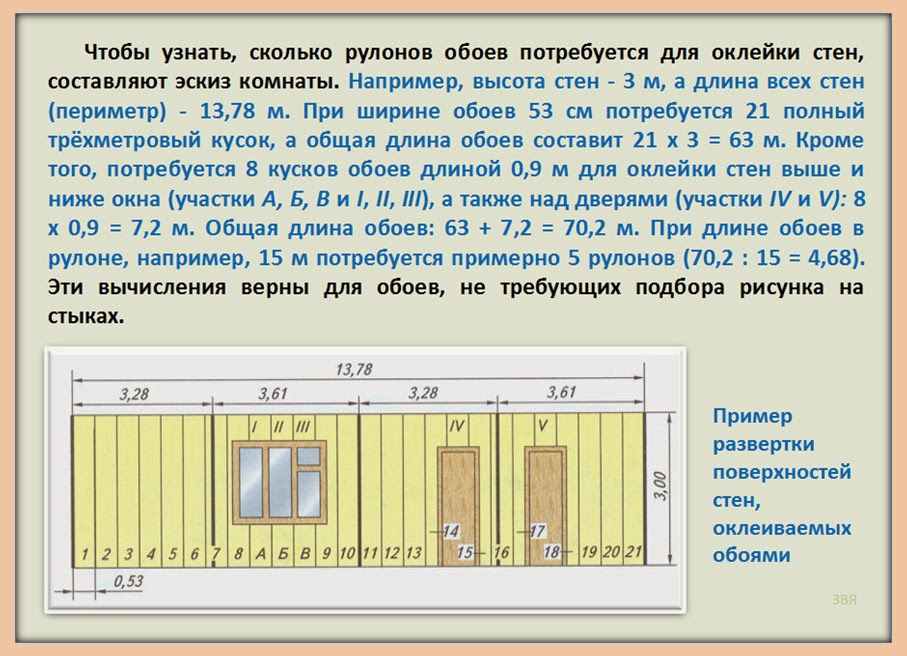 Рассмотрим несколько примеров:
Рассмотрим несколько примеров:
Пример 1. Выразить 1 квадратный метр в квадратных сантиметрах.
1 квадратный метр это квадрат со стороной 1 м. То есть все четыре стороны имеют длину, равную одному метру.
Но 1 м = 100 см. Тогда все четыре стороны тоже имеют длину, равную 100 см
Вычислим новую площадь этого квадрата. Умножим длину 100 см на ширину 100 см или возведём в квадрат число 100
S = 1002 = 10 000 см2
Получается, что на один квадратный метр приходится десять тысяч квадратных сантиметров.
1 м2 = 10 000 см2
Это позволяет в будущем умножить любое количество квадратных метров на 10 000 и получить площадь, выраженную в квадратных сантиметрах.
Чтобы перевести квадратные метры в квадратные сантиметры, нужно количество квадратных метров умножить на 10 000.
А чтобы перевести квадратные сантиметры в квадратные метры, нужно наоборот количество квадратных сантиметров разделить на 10 000.
Например, переведём 100 000 см2 в квадратные метры. Рассуждать в этом случае можно так: «если 10 000 см2 это один квадратный метр, то сколько раз 100 000 см2 будут содержать по 10 000 см2»
100 000 см2 : 10 000 см2 = 10 м2
Другие единицы измерения можно переводить таким же образом. Например, переведём 2 км2 в квадратные метры.
Один квадратный километр это квадрат со стороной 1 км. То есть все четыре стороны имеют длину, равную одному километру. Но 1 км = 1000 м. Значит, все четыре стороны квадрата также равны 1000 м. Найдём новую площадь квадрата, выраженную в квадратных метрах. Для этого умножим длину 1000 м на ширину 1000 м или возведём в квадрат число 1000
S = 10002 = 1 000 000 м2
Получается, что на один квадратный километр приходится один миллион квадратных метров:
1 км2 = 1 000 000 м2
Это позволяет в будущем умножить любое количество квадратных километров на 1 000 000 и получить площадь, выраженную в квадратных метрах.
Чтобы перевести квадратные километры в квадратные метры, нужно количество квадратных километров умножить на 1 000 000.
Итак, вернёмся к нашей задаче. Требовалось перевести 2 км2 в квадратные метры. Умножим 2 км2 на 1 000 000
2 км2 × 1 000 000 = 2 000 000 м2
А чтобы перевести квадратные метры в квадратные километры, нужно наоборот количество квадратных метров разделить на 1 000 000.
Например, переведём 3 500 000 м2 в квадратные километры. Рассуждать в этом случае можно так: «если 1 000 000 м2 это один квадратный километр, то сколько раз 3 500 000 м2 будут содержать по 1 000 000 м2»
3 500 000 м2 : 1 000 000 м2 = 3,5 км2
Пример 2. Выразить 7 м2 в квадратных сантиметрах.
Умножим 7 м2 на 10 000
7 м2 = 7 м2 × 10 000 = 70 000 см2
Пример 3. Выразить 5 м2 13 см2 в квадратных сантиметрах.
Выразить 5 м2 13 см2 в квадратных сантиметрах.
5 м2 13 см2 = 5 м2 × 10 000 + 13 см2 = 50 013 см2
Пример 4. Выразить 550 000 см2 в квадратных метрах.
Узнаем сколько раз 550 000 см2 содержит по 10 000 см2. Для этого разделим 550 000 см2 на 10 000 см2
550 000 см2 : 10 000 см2 = 55 м2
Пример 5. Выразить 7 км2 в квадратных метрах.
Умножим 7 км2 на 1 000 000
7 км2 × 1 000 000 = 7 000 000 м2
Пример 6. Выразить 8 500 000 м2 в квадратных километрах.
Узнаем сколько раз 8 500 000 м2 содержит по 1 000 000 м2. Для этого разделим 8 500 000 м2 на 1 000 000 м2
8 500 000 м2 × 1 000 000 м2 = 8,5 км2
Единицы измерения площади земельных участков
Площади небольших земельных участков удобно измерять в квадратных метрах.
Площади более крупных земельных участков измеряются в арах и гектарах.
Ар (сокращённо: a) — это площадь равная ста квадратным метрам (100 м2). В виду частого распространения такой площади (100 м2) она стала использоваться, как отдельная единица измерения.
Например, если сказано что площадь какого-нибудь поля составляет 3 а, то нужно понимать, что это три квадрата площадью 100 м2 каждый, то есть:
3 а = 100 м2 × 3 = 300 м2
В народе ар часто называют соткой, поскольку ар равен квадрату, площадью 100 м2. Примеры:
1 сотка = 100 м2
2 сотки = 200 м2
10 соток = 1000 м2
Гектар (сокращенно: га) — это площадь, равная 10 000 м2. Например, если сказано что площадь какого-нибудь леса составляет 20 гектаров, то нужно понимать, что это двадцать квадратов площадью 10 000 м2 каждый, то есть:
20 га = 10 000 м2 × 20 = 200 000 м2
Прямоугольный параллелепипед и куб
Прямоугольный параллелепипед — это геометрическая фигура, состоящая из грáней, рёбер и вершин. На рисунке показан прямоугольный параллелепипед:
На рисунке показан прямоугольный параллелепипед:
Желтым цветом показаны грáни параллелепипеда, чёрным цветом — рёбра, красным — вершины.
Прямоугольный параллелепипед обладает длиной, шириной и высотой. На рисунке показано где длина, ширина и высота:
Параллелепипед, у которого длина, ширина и высота равны между собой, называется кубом. На рисунке показан куб:
Объём геометрической фигуры
Объём геометрической фигуры — это число, которое характеризует вместимость данной фигуры.
Объём измеряется в кубических единицах. Под кубическими единицами подразумевают кубы длиной 1, шириной 1 и высотой 1. Например, 1 кубический сантиметр или 1 кубический метр.
Измерить объём какой-нибудь фигуры означает выяснить сколько кубических единиц вмещается в данную фигуру.
Например, объём следующего прямоугольного параллелепипеда равен двенадцати кубическим сантиметрам:
Это потому что в данный параллелепипед вмещается двенадцать кубов длиной 1 см, шириной 1 см и высотой 1 см:
Объём обозначается заглавной латинской буквой V. Одна из единиц измерения объема это кубический сантиметр (см3). Тогда объём V рассмотренного нами параллелепипеда равен 12 см3
Одна из единиц измерения объема это кубический сантиметр (см3). Тогда объём V рассмотренного нами параллелепипеда равен 12 см3
V = 12 см3
Объём любого параллелепипеда вычисляют следующим образом: перемножают его длину, ширину и высоту .
Объём прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.
V = abc
где, a — длина, b — ширина, c — высота
Так, в предыдущем примере мы визуально определили, что объём параллелепипеда равен 12 см3. Но можно измерить длину, ширину и высоту данного параллелепипеда и перемножить результаты измерений. Мы получим тот же результат
Объём куба вычисляется таким же образом, как и объём прямоугольного параллелепипеда — перемножают длину, ширину и высоту.
Например, вычислим объём куба, длина которого 3 см. У куба длина, ширина и высота равны между собой. Если длина равна 3 см, то равны этим же трём сантиметрам ширина и высота куба:
У куба длина, ширина и высота равны между собой. Если длина равна 3 см, то равны этим же трём сантиметрам ширина и высота куба:
Перемножаем длину, ширину, высоту и получаем объём, равный двадцати семи кубическим сантиметрам:
V = 3 × 3 × 3 = 27 см³
Действительно, в исходный куб вмещается 27 кубиков длиной 1 см
При вычислении объёма данного куба мы перемножили длину, ширину и высоту. Получилось произведение 3 × 3 × 3. Это есть произведение трёх сомножителей, каждый из которых равен 3. Иными словами, произведение 3 × 3 × 3 является третьей степенью числа 3 и может быть записано в виде 33.
V = 33 = 27 см3
Поэтому третью степень числа называют кубом числа. При вычислении третьей степени числа a, человек тем самым находит объём куба, длиной a. Операцию возведения числа в третью степень по другому называют возведением в куб.
Таким образом, объём куба вычисляется по следующему правилу:
V = a3
Где a — длина куба.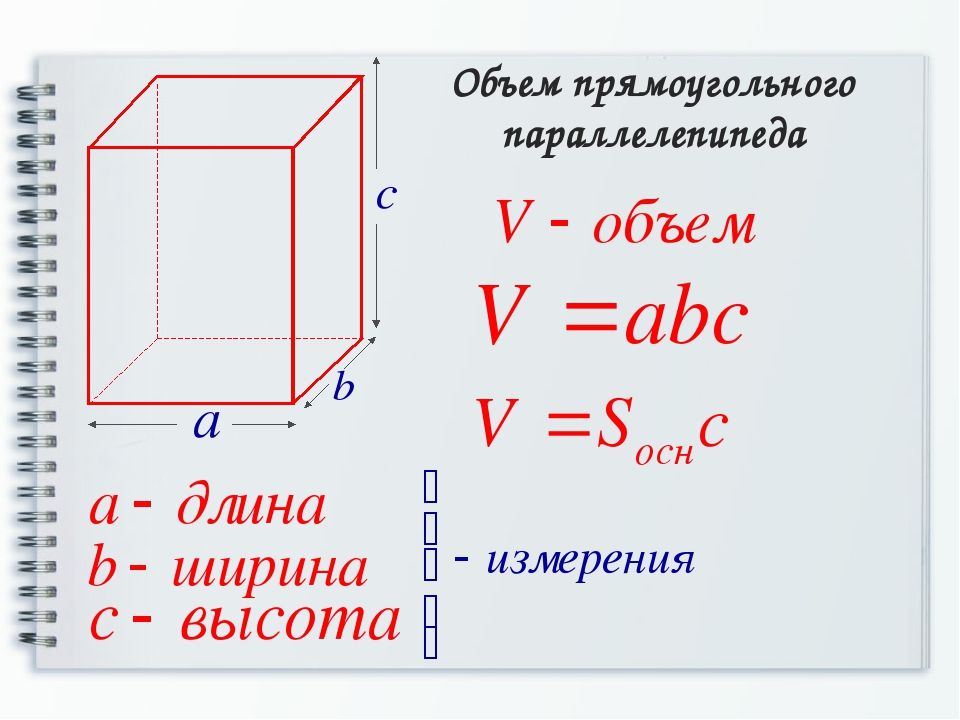
Кубический дециметр. Кубический метр
Не все объекты нашего мира удобно измерять в кубических сантиметрах. Например, объём комнаты или дома удобнее измерять в кубических метрах (м3). А объём бака, аквариума или холодильника удобнее измерять в кубических дециметрах (дм3).
Другое название одного кубического дециметра – один литр.
1 дм3 = 1 литр
Перевод единиц измерения объёма
Единицы измерения объёма можно переводить из одной единицы измерения в другую. Рассмотрим несколько примеров:
Пример 1. Выразить 1 кубический метр в кубических сантиметрах.
Один кубический метр это куб со стороной 1 м. Длина, ширина и высота этого куба равны одному метру.
Но 1 м = 100 см. Значит, длина, ширина и высота тоже равны 100 см
Вычислим новый объём куба, выраженный в кубических сантиметрах. Для этого перемножим его длину, ширину и высоту. Либо возведём число 100 в куб:
V = 1003 = 1 000 000 см3
Получается, что на один кубический метр приходится один миллион кубических сантиметров:
1 м3 = 1 000 000 см3
Это позволяет в будущем умножить любое количество кубических метров на 1 000 000 и получить объём, выраженный в кубических сантиметрах.
Чтобы перевести кубические метры в кубические сантиметры, нужно количество кубических метров умножить на 1 000 000.
А чтобы перевести кубические сантиметры в кубические метры, нужно наоборот количество кубических сантиметров разделить на 1 000 000.
Например, переведём 300 000 000 см3 в кубические метры. Рассуждать в этом случае можно так: «если 1 000 000 см3 это один кубический метр, то сколько раз 300 000 000 см3 будут содержать по 1 000 000 см3»
300 000 000 см3 : 1 000 000 см3 = 300 м3
Пример 2. Выразить 3 м3 в кубических сантиметрах.
Умножим 3 м3 на 1 000 000
3 м3 × 1 000 000 = 3 000 000 см3
Пример 3. Выразить 60 000 000 см3 в кубических метрах.
Узнаем сколько раз 60 000 000 см3 содержит по 1 000 000 см3. Для этого разделим 60 000 000 см3 на 1 000 000 см3
Для этого разделим 60 000 000 см3 на 1 000 000 см3
60 000 000 см3 : 1 000 000 см3 = 60 м3
Вместимость бака, банки или канистры измеряют в литрах. Литр это тоже единица измерения объема. Один литр равен одному кубическому дециметру.
1 литр = 1 дм3
Например, если вместимость банки составляет 1 литр, это значит что объём этой банки составляет 1 дм3. При решении некоторых задач может быть полезным умение переводить литры в кубические дециметры и наоборот. Рассмотрим несколько примеров.
Пример 1. Перевести 5 литров в кубические дециметры.
Чтобы перевести 5 литров в кубические дециметры, достаточно умножить 5 на 1
5 л × 1 = 5 дм3
Пример 2. Перевести 6000 литров в кубические метры.
Шесть тысяч литров это шесть тысяч кубических дециметров:
6000 л × 1 = 6000 дм3
Теперь переведём эти 6000 дм3 в кубические метры.
Длина, ширина и высота одного кубического метра равны 10 дм
Если вычислить объём этого куба в дециметрах, то получим 1000 дм3
V = 103= 1000 дм3
Получается, что одна тысяча кубических дециметров соответствует одному кубическому метру. А чтобы определить сколько кубических метров соответствуют шести тысячамл кубических дециметров, нужно узнать сколько раз 6 000 дм3 содержит по 1 000 дм3
6 000 дм3 : 1 000 дм3 = 6 м3
Значит, 6000 л = 6 м3.
Таблица квадратов
В жизни часто приходиться находить площади различных квадратов. Для этого каждый раз требуется возводить исходное число во вторую степень.
Квадраты первых 99 натуральных чисел уже вычислены и занесены в специальную таблицу, называемую таблицей квадратов.
Первая строка данной таблицы (цифры от 0 до 9) это единицы исходного числа, а первый столбец (цифры от 1 до 9) это десятки исходного числа.
Например, найдём квадрат числа 24 по данной таблице. Число 24 состоит из цифр 2 и 4. Точнее, число 24 состоит из двух десятков и четырёх единиц.
Итак, выбираем цифру 2 в первом столбце таблицы (столбце десятков), а цифру 4 выбираем в первой строке (строке единиц). Затем, двигаясь вправо от цифры 2 и вниз от цифры 4, найдём точку пересечения. В результате окажемся на позиции, где располагается число 576. Значит, квадрат числа 24 есть число 576
242 = 576
Таблица кубов
Как и в ситуации с квадратами, кубы первых 99 натуральных чисел уже вычислены и занесены в таблицу, называемую таблицей кубов.
Куб числа по таблице определяется таким же образом, как и квадрат числа. Например, найдём куб числа 35. Это число состоит из цифр 3 и 5. Выбираем цифру 3 в первом столбце таблицы (столбце десятков), а цифру 5 выбираем в первой строке (строке единиц). Двигаясь вправо от цифры 3 и вниз от цифры 5, найдём точку пересечения. В результате окажемся на позиции, где располагается число 42875. Значит, куб числа 35 есть число 42875.
353 = 42875
Задания для самостоятельного решения
Задача 1. Длина прямоугольника составляет 6 см, а ширина 2 см. Найдите периметр.
Решение
P = 2(a + b)
a = 6, b = 2
P = 2(6 + 2) = 12 + 4 = 16 см
Ответ: периметр прямоугольника равен 16 см.
Задача 2. Длина прямоугольника составляет 6 см, а ширина 2 см. Найдите площадь.
Решение
S = ab
a = 6, b = 2
S = 6 × 2 = 12 см2
Ответ: площадь равна 12 см2.
Задача 3. Площадь прямоугольника составляет 12 см2. Длина составляет 6 см. Найдите ширину прямоугольника.
Решение
S = ab
S = 12, a = 6, b = x
12 = 6 × x
x = 2
Ответ: ширина прямоугольника составляет 2 см.
Задача 4. Вычислите площадь квадрата со стороной 8 см
Решение
S = a2
a = 8
S = 82 = 64 см2
Ответ: площадь квадрата со стороной 8 см равна 64 см2
Задача 5. Вычислите объем прямоугольного параллелепипеда, длина которого 6 см, ширина 4 см, высота 3 см.
Решение
V = abc
a = 6, b = 4, c = 3
V = 6 × 4 × 3 = 72 см3.
Ответ: объем прямоугольного параллелепипеда, длина которого 6 см, ширина 4 см, высота 3 см равен 72 см3
Задача 6. Объем прямоугольного параллелепипеда составляет 200 см3. Найдите высоту параллелепипеда, если его длина равна 10 см, а ширина 5 см
Решение
V = abc
V = 200, a = 10, b = 5, c = x
200 = 10 × 5 × x
200 = 50x
x = 4
Ответ: высота прямоугольного параллелепипеда равна 4 см.
Задача 7. Площади земельного участка, засеянные пшеницей и льном, пропорциональны числам 4 и 5. На какой площади засеяна пшеница, если под льном засеяно 15 га
Решение
Число 4 отражает площадь, засеянную пшеницей. А число 5 отражает площадь, засеянную льном.
Сказано что площади, засеянные пшеницей и льном пропорциональны этим числам.
Проще говоря, во сколько раз изменяются числа 4 или 5, во сколько же раз изменится и площадь, которая засеяна пшеницей или льном. Льном засеяно 15 га. То есть число 5, которое отражает площадь, засеянную льном, изменилось в 3 раза.
Тогда число 4, которое отражает площадь засеянную пшеницей, нужно увеличить в три раза
4 × 3 = 12 га
Ответ: пшеницей засеяно 12 га.
Задача 8. Длина зернохранилища 42 м, ширина составляет длины, а высота – 0,1 длины. Определите сколько тонн зерна вмещает зернохранилище, если 1 м3 его весит 740 кг.
Решение
a — длина
b — ширина
c — высота
a = 42 м
b = м
c = 42 × 0,1 = 4,2 м
Определим объем зернохранилища:
V = abc = 42 × 30 × 4,2 = 5292 м3
Определите сколько тонн зерна вмещает зернохранилище:
5292 × 740 = 3916080 кг
Переведём килограммы в тонны:
Ответ: зернохранилище вмещает 3916,08 тонн зерна.
Задача 9. 12. Бассейн имеет форму прямоугольного параллелепипеда, длина которого равна 5,8 м, а ширина – 3,5 м. Две трубы наполняют его водой в течение 13 ч 32 мин., причём через одну из них вливается 25 л/мин, а через вторую – 0,75 этого количества. Определите высоту (глубину) бассейна.
Решение
Определим сколько литров в минуту вливается через вторую трубу:
25 л/мин × 0,75 = 18,75 л/мин
Определим сколько литров в минуту вливается в бассейн через обе трубы:
25 л/мин + 18,75 л/мин = 43,75 л/мин
Определим сколько литров воды будет залито в бассейн за 13 ч 32 мин
43,75 × 13 ч 32 мин = 43,75 × 812 мин = 35 525 л
1 л = 1 дм3
35 525 л = 35 525 дм3
Переведём кубические дециметры в кубические метры. Это позволит вычислит объем бассейна:
35 525 дм3 : 1000 дм3 = 35,525 м3
Зная объём бассейна можно вычислить высоту бассейна. Подставим в буквенное уравнение V=abc имеющиеся у нас значения. Тогда получим:
V = 35,525
a = 5.8
b = 3.5
c = x
35,525 = 5,8 × 3,5 × x
35,525 = 20,3 × x
x = 1,75 м
с = 1,75
Ответ: высота (глубина) бассейна составляет 1,75 м.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Как посчитать квадратуру комнаты, стен, потолка, пола
Временами требуется узнать площадь или объем комнаты, чтобы произвести расчеты на приобретение различных материалов для строительства или ремонта помещения. В процессе ремонта приходится измерять площадь стен, чтобы определиться с количеством обоев или других отделочных материалов. Как правило, расчеты начинаются с замеров. Замеры осуществляются с помощью рулетки или другими способами.
Как посчитать площадь комнаты?
Это не сложный процесс, поскольку существуют определенные формулы. В данном случае, достаточно определиться с размерами. Для этого необходимо:
- приобрести рулетку, самую обычную, желательно на 5 метров;
- взять бумагу, карандаш или ручку;
- иметь калькулятор, хотя не сложно посчитать и на бумаге.
С помощью этого, минимального набора приспособлений и осуществляются все необходимые расчеты. Лучше конечно, иметь помощника, но, в крайнем случае, можно все делать самому. Габариты комнаты измеряются вдоль стен, если они не заставлены мебелью. Если нужны точные размеры, то лучше мебель отставить и освободить стены. Лишь после этого рекомендуется производить все измерения. При этом, следует учитывать тот фактор, что правильных комнат, с прямыми углами практически не существует, если дело касается помещений, сооруженных еще в советские времена. В связи с этим, необходимо весьма серьезно отнестись к процессу измерения.
Прямоугольные помещения
Если комната имеет правильную (относительно) прямоугольную форму, без всевозможных выступов или ниш, то площадь ее вычисляется довольно просто. Для начала, нужно измерить длину и ширину комнаты, после чего результаты записать на бумажке, чтобы не забыть. Измерения можно производить как в метрах, так и в сантиметрах. Если замеры осуществляются в метрах, то после целых значений метров ставится запятая, а потом пишутся сантиметры. Например, 4 метра, 35 сантиметров следует записать: 4,35 м.
Измерив длину, например, 2,35 м и ширину 1,4 м, данные перемножаются. Например: 2,35 м х 1,4 м. В результате получается 3,290 м2 или 3,29 м2. Как правило, после запятой всегда оставляется две цифры. Если их больше, то значение округляется по правилам, которые излагались еще в начальных классах школы. При этом, можно округлять или до метров, или до сантиметров, в зависимости от требуемой точности. В основном, достаточно измерять с точностью до метров и лишь изредка требуется точность до сантиметров.
Комната неправильной формы
Не все комнаты имеют правильную форму. Довольно часто встречаются помещения с наличиями выступов различной формы. В таких случаях, помещения делятся на отдельные квадраты, прямоугольники или треугольники, в зависимости от конфигурации выступов. Затем измеряются все выступы, после чего рассчитывают их площадь и все полученные результаты суммируют.
На фото выше представлен пример, где в комнате имеется выступ прямоугольной формы. В таком случае, площадь комнаты вычисляется следующим образом:
- Подсчитывается общая площадь без выступа: 3,6м х 8,5м = 30,6м2.
- Вычисляется площадь выступа: 3,25м х 0,8м = 2,6м2.
- Полученные результаты складываются: 30,6м2 + 2,6м2 = 33,2м2.
Встречаются комнаты со скошенными стенами. Поступают следующим образом: стена разбивается так, что получается прямоугольник и треугольник (см. рисунок ниже). В результате для расчетов, необходимо иметь пять размеров. Впоследствии, вычисляют отдельно площади фигур, а потом все результаты либо складывают, либо вычитаются, в зависимости от характера выступа.
Квадратуру обсчитывают в таком порядке:
- Подсчитывается основная прямоугольная часть: 6,5 м х 1,4 м = 8,96м2. Округляя получаем 9,0 м2.
- Вычисляется площадь малого прямоугольника: 2,7м х 1,9м = 5,13м2. При округлении получаем 5,0 м2.
- Подсчитывается площадь треугольника, имеющего прямой угол (1,3м х 1,9м) / 2 = 1,235м2. Округлив получится 1 м2.
- В заключение, полученные результаты складываются: 9+5+1 = 15 м2.
Подобная точность вычислений абсолютно приемлема. Как правило, планировка помещений бывает разнообразной, но правило подсчетов абсолютно одинаковы: все делится на отдельные, независимые фигуры, подсчитывается площадь отдельных фигур, а потом все складывается, а может и вычитается, в зависимости от конфигурации выступов. Особенно это актуально при определении площади пола или потолка.
Как подсчитать площадь стен
Квадратуру стен необходимо знать, когда планируется закупка отделочных материалов, таких как обои, шпаклевка, краска и другие. Если это глухая стена, то здесь все просто – измеряется высота и длина стены, после чего результаты перемножаются. Если в стене расположен оконный или дверной проем, то нужно определить, какую площадь они занимают и отнять от общей площади стены. Поэтому:
- измеряют высоту стен и их ширину;
- узнают высоту и ширину дверных проемов;
- измеряют высоту и ширину оконных проемов.
Глухая стена
- 2,5 м х 6,0м = 15 м2 – площадь глухой стены.
Стена с дверным проемом:
- Общая площадь стены: 2,5м х 6,0м = 15м2.
- Площадь дверного проема: 2,1м х 1,0м = 2,1м2.
- Площадь стены без дверей: 15м2 – 2,1м2 = 12,9м2.
Стена с оконным проемом:
- Общая площадь стены: 2,5м х 4м = 10м2.
- Площадь оконного проема: 1,3м х 1,5м = 1,95м2.
- Площадь стены без окна: 10 м2 – 1,95 м2 = 8,05м2.
Как правило, вычисляют общую площадь всех стен. Для этого берут и складывают полученные результаты площадей каждой стены. Например: 15м2 + 12,9м2 + 10м2 + 8,05м2 = 45,95м2.
Как определить объем комнаты
Иногда, для некоторых расчетов необходимо знать, какой объем занимает комната. Для подобных расчетов нужно знать еще одну цифру: не только длину и ширину, но и высоту комнаты. В результате расчетов получается кубатура (объем) комнаты, которая обозначается в метрах кубических. Например:
- длина помещения – 6 м;
- ширина помещения – 4 м;
- высота помещения – 2,5 м.
Теперь нужно все показатели перемножить: 6м х 4м х 2,5м = 60м3. Итак, получается, что объем помещения составляет 60 м3.
Заключение
Подобная точность расчетов на конечный результат особо не влияет, поскольку мало кто приобретает облицовочные материалы исходя из подобных расчетов. Как правило, приобретают любые облицовочные материалы с некоторым запасом. Если, например, считают количество керамической плитки, то расчеты производят по количеству штук, исходя из схемы укладки. Даже в этом случае, ее берут с некоторым избытком. Это связано еще и с тем, что возможны нештатные ситуации, связанные с порчей облицовочного материала. Особенно это актуально, когда работы выполняются самостоятельно, без привлечения профессионалов.
Это относится и к таким материалам, как обои, линолеум, ламинат, различная вагонка, сайдинг и т.д. Нужно всегда помнить, что при работах появляются отходы и, причем, их может быть немало, если размеры произвольные, без учета применения тех или иных материалов.
Подобный подход особенно актуален при укладке линолеума, который имеет стандартные размеры по ширине. Что касается его длины, то тут нужно очень точно все измерить и всегда сантиметров 10, но добавить. Если просчитаться, то это может дорого обойтись.
Размер и объем комнаты — Акустические поля
Ниже приводится неотредактированная стенограмма из нашей серии видео с Acoustic Fields. В процессе перевода могут возникнуть некоторые ошибки в грамматике и структуре предложения. Для полного понимания и понимания, пожалуйста, просмотрите видео, которое включено в этот текст. Этот блог был обновлен 05.12.19, чтобы отразить изменения в опыте и знаниях в отношении размера комнаты.
______
Всем привет, Деннис Фоули из Acoustic Fields.Сегодня мы поговорим о размере и объеме комнаты, так как я получаю много вопросов по этому поводу, и меня никогда не перестает удивлять, сколько, сколько непониманий существует по этому поводу. Так что я как бы собрал здесь несколько рекомендаций, и, возможно, это немного поможет ситуации.
Коробка давления
Что это за комната? Комната — это действительно огромный ящик давления. Ну, в некоторых случаях не очень большой. Но это коробка давления от наших громкоговорителей или чего-то еще, живая комната, управление, голос.Это коробка, которая должна содержать в себе всю вложенную в нее энергию и управлять ею, если вы собираетесь достичь определенных результатов. В живой комнате вы хотите записывать определенные вещи, вы хотите, чтобы они звучали определенным образом. В диспетчерской, в комнате микширования и мастеринга, вам нужен перевод. Таким образом, каждое использование комнаты имеет конкретную цель, которую вы должны достичь. И размер и объем комнаты имеют решающее значение для этой коробки давления. Очевидно, чем меньше мы сделаем коробку, и если мы будем поддерживать постоянное давление, у нас будут проблемы.Очевидно, если мы будем продолжать увеличивать давление и уменьшать объем коробки, мы можем просто застрелиться, потому что такие отношения не будут работать вообще.
Объем помещения
Итак, как рассчитать объем помещения — длину, ширину и высоту? Хорошая простая формула. Возьмите длину вашей комнаты, ширину вашей комнаты и высоту вашей комнаты и умножьте на три. Это даст вам ваш кубический объем, кубические футы объема. Если у вас заграничный кубический объем, вам просто нужно вбить это число в голову.Я просмотрел нашу базу данных и выделил три подразделения. У нас есть 206 комнат, построенных и измеренных в нашей базе данных, я взял все эти комнаты и разбил их на три части, и я думаю, что эти три области помогут. Все они основаны на объеме.
Красная зона Комната
Итак, если длина, ширина и высота вашей комнаты меньше 1500 футов, пожалуйста, кубических футов, пожалуйста, найдите другую комнату. Почему я это говорю? Он слишком мал для того, чтобы правильно управлять какой-либо энергией.Возьмем низкочастотную энергию. Если вы собираетесь управлять низкими частотами в комнате менее 1500 кубических футов, объем обработки, который вы должны провести в комнате, сделает ее настолько маленькой, что вы не сможете в ней сидеть. Так что меньше 1500 кубических футов — это абсолютно не так. Найдите другую комнату.
Комната желтой зоны
Менее 3000 кубических футов. Теперь они могут быть разными, вы знаете длину, ширину и высоту, все они могут быть разными. Но мы смотрим на кубические футы, потому что здесь мы говорим о ящике давления.Так что меньше 3000 кубических футов, проблематично. Да, это лечится. Да, с этим можно справиться в зависимости от использования и того, чего вы пытаетесь достичь в этой комнате. Менее 3000 кубических футов годятся для одних видов использования, но не подходят для других. Так что это — когда я называю проблемным, это поддается лечению, в зависимости от использования. И вы должны выяснить, что вы пытаетесь сделать в комнате, в сравнении с тем, сколько процедур вам потребуется в этой комнате.
Номер «Зеленая зона» — лучший
Следующий больше 4500 кубических футов.Все, что превышает 4500 кубических футов, поддается лечению и может использоваться практически во всех формах и сферах использования. Итак, это даст вам некоторое представление о трех разных уровнях, на которые стоит взглянуть. Если вы рассматриваете комнату для дополнительного использования, посмотрите на длину, ширину и высоту, получите объем, посмотрите на эту диаграмму, и я собираюсь включить диаграмму в конце, чтобы вы могли ее визуализировать. И просто посмотрите, где находятся ваши размеры в этой таблице, и поймите, что если оно меньше 1500 кубических футов, найдите другую комнату. Просто сделай это, тебе будет намного лучше.Менее 3000 кубических футов, мы можем это лечить. Это проблематично, у нас есть проблемы с давлением, у нас есть проблемы со временем реверберации RT 60, но это поддается лечению в зависимости от использования. Теперь есть квалификация для использования. Возможно, это не сработает для концертной комнаты с барабанами, но может сработать для голосовой или диспетчерской. Так что все зависит от использования. 4500 кубических футов и больше, много места, много места для управления низкочастотным давлением и отражениями или RT 60 раз. На этом графике, о котором я говорю, вы можете видеть разбивку, и у нас она окрашена в красный, желтый и зеленый цвета.Красный не подходит для акустики, а желтый — проблематичен в зависимости от использования. Так что помните об этой таблице и часто обращайтесь к ней, если вы смотрите на использование, давление и объем в комнатах.
Низкая частота
Наша первая проблема в любом небольшом помещении — это низкочастотная энергия. Волны низкочастотной энергии длинные и высокие, и большинство из них не поместятся в наших комнатах. Когда они не подходят, они искажают комнату. Это искажение называется модами. У нас есть осевые моды, которые представляют собой низкочастотную энергию, которая проходит между двумя параллельными стенками.Это могут быть боковые стенки, боковины, передние и задние стены и даже пол до потолка. Наш следующий набор искажений — это тангенциальные моды. Это энергия, которая не умещается между четырьмя стенами в объеме комнаты. Наконец, у нас есть наклонные моды, которые представляют собой шесть искажений площади поверхности.
Частота Vs. Длина волны 20 Гц — 90 Гц
Модальное искажение
Когда низкочастотная энергия не подходит, возникает искажение. На что похоже это искажение? Искажение из-за волн энергии, которые не вписываются в размеры вашей комнаты, заставляет воздух между этими поверхностями вибрировать.Когда воздух колеблется между нашими поверхностными областями в нашей небольшой комнате, мы будем слышать слишком много определенной частоты или мы не будем слышать ни одной из этих частот. Все мы слышали «бас-бум». Это искаженный звук низкочастотной энергии, не помещающийся в наших комнатах. Это преувеличенный звук. Другие звуки могут быть не слышны. Возбуждение воздуха не позволит нам услышать определенные волны энергии, которые не поместятся в комнате.
Кривая частотной характеристики: https: // en.wikipedia.org/wiki/Frequency_response
На этом графике частотной характеристики мы видим большой пик ниже 100 Гц. Это указывает на то, что у нас будет чрезмерная энергия в этом частотном диапазоне. Это будет преувеличенный звук, похожий на наш пример с «басовой стрелой». В этом частотном диапазоне слишком много энергии, чтобы соответствовать размерам и объему комнаты. Обратите внимание на другие провалы или впадины на кривой частотной характеристики. Эти провалы означают, что вы не будете слышать звуки на этих частотах.Энергия определенной длины волны не подходит, а когда она не подходит, она производит преувеличенные звуки или вообще не производит звуков.
Низкочастотное лечение
Для пиков на нашем графике и в комнате мы должны использовать низкочастотное поглощение. Существует три типа низкочастотного поглощения. Бывают Гельмгольца, Мембранные и Диафрагмальные. Диафрагма является самой мощной и поглощает больше избыточной энергии, показанной выше 100 Гц. Он будет опускаться ниже в частотном диапазоне и поглощать больше энергии на квадратный фут, чем любой из двух других типов.Пространство для лечения проблем с низкими частотами ограничено в наших маленьких комнатах, поэтому мы должны использовать тип и количество лечения, которые имеют требуемую скорость и уровни, чтобы справиться с избыточной энергией, показанной выше ниже 100 Гц.
Диафрагмальное поглощение: https://acousticfields.com/product-category/sound-absorption/acda-series/
Средние / высокие частоты
Энергия средних и высоких частот, показанная на приведенной выше кривой отклика, может быть обработана с использованием технологии вспенивания с открытыми ячейками.Это самый экономичный и простой в установке из всех видов лечения. Поставляется в виде панелей, которые можно повесить на поверхность стены. Вы должны рассчитать, сколько площади вашей комнаты требуется для решения ваших конкретных задач, а затем установить панели, которые имеют необходимую площадь поверхности, чтобы справиться с частотными искажениями.
Акустические панели
: https://acousticfields.com/product/acoustic-panels/
Спасибо,
Деннис Фоли
Расчетный объем | SkillsYouNeed
На этой странице объясняется, как рассчитать объем твердых объектов, т.е.е. насколько вы могли бы поместиться в предмет, если бы, например, вы залили его жидкостью.
Площадь — это мера того, сколько места находится внутри двухмерного объекта (подробнее см. Нашу страницу: Расчет площади).
Объем — это мера пространства внутри трехмерного объекта. Наша страница, посвященная трехмерным формам, объясняет основы таких форм.
В реальном мире вычисление объема, вероятно, не то, что вы будете использовать так часто, как вычисление площади.
Однако это все еще может быть важным. Возможность рассчитать объем позволит вам, например, определить, сколько места для упаковки у вас есть при переезде, сколько офисного пространства вам нужно или сколько варенья вы можете уместить в банку.
Это также может быть полезно для понимания того, что имеют в виду средства массовой информации, когда говорят о пропускной способности плотины или течении реки.
Примечание к единицам
Площадь выражается в квадратных единицах, потому что это два измерения, умноженные вместе.
Объем выражается в кубических единицах, потому что это сумма трех измерений (длина, ширина и глубина), умноженных вместе. Кубические единицы включают см 3 , м 3 и кубические футы.
ВНИМАНИЕ!
Объем также можно выразить как вместимость по жидкости.
Метрическая система
В метрической системе объем жидкости измеряется в литрах, что напрямую сопоставимо с кубическим размером, так как 1 мл = 1 см 3 .1 литр = 1000 мл = 1000 см 3 .
Британская / Британская система
В британской / британской системе эквивалентными измерениями являются жидкие унции, пинты, кварты и галлоны, которые нелегко перевести в кубические футы. Поэтому лучше придерживаться жидких или твердых единиц объема.
Дополнительную информацию см. На нашей странице Системы измерения
Основные формулы для расчета объема
Объем прямоугольных тел
В то время как основная формула для площади прямоугольной формы — длина × ширина, основная формула для объема — длина × ширина × высота.
То, как вы относитесь к различным размерам, не меняет расчет: например, вы можете использовать «глубину» вместо «высоты». Важно то, что три измерения умножаются. Вы можете умножать в любом порядке, поскольку это не изменит ответ (подробнее см. Нашу страницу о умножении ).
Коробка размером 15 см в ширину, 25 см в длину и 5 см в высоту имеет объем:
15 × 25 × 5 = 1875 см 3
Объем призм и цилиндров
Эту базовую формулу можно расширить, чтобы охватить объем цилиндров и призм .Вместо прямоугольного конца у вас просто другая форма: круг для цилиндров, треугольник, шестиугольник или любой другой многоугольник для призмы.
Фактически, для цилиндров и призм объем — это площадь одной стороны, умноженная на глубину или высоту формы.
Таким образом, основная формула для определения объема призм и цилиндров:
Площадь формы торца × высота / глубина призмы / цилиндра.
Объем конусов и пирамид
Тот же принцип, что и выше (ширина × длина × высота), применяется для вычисления объема конуса или пирамиды, за исключением того, что, поскольку они достигают точки, объем составляет лишь часть от общего количества, которое было бы, если бы они продолжались в той же форме насквозь.
Объем конуса или пирамиды составляет ровно одну треть от объема коробки или цилиндра с таким же основанием.
Таким образом, формула:
Площадь основания или торца × высота конуса / пирамиды × 1 / 3
Вернитесь на нашу страницу Расчет площади , если вы не можете вспомнить, как рассчитать площадь круга или треугольника.
Например, чтобы вычислить объем конуса с радиусом 5 см и высотой 10 см:
Площадь внутри круга = πr2 (где π (пи) приблизительно равно 3.14 и r — радиус окружности).
В этом примере площадь основания (круга) = πr 2 = 3,14
× 5 × 5 = 78,5 см 2 .78,5 × 10 = 785
785 × 1/3 = 261,6667 см 3
Объем сферы
Как и в случае с кругом, вам нужно π (пи) для вычисления объема сферы.
Формула: 4/3 × π × радиус 3 .
Вам может быть интересно, как определить радиус шара.Если не протыкать через него спицу (эффективный, но конечный для мяча!), Есть способ попроще.
Вы можете измерить расстояние вокруг самой широкой точки сферы напрямую, например, с помощью рулетки. Этот круг является окружностью и имеет тот же радиус, что и сама сфера.
Длина окружности вычисляется как радиус 2 x π x.
Чтобы вычислить радиус из окружности, вы:
Разделите окружность на (2 x π) .
Рабочие примеры: Расчет объема
Пример 1
Вычислите объем цилиндра длиной 20 см, круговой конец которого имеет радиус 2,5 см.
Сначала проработайте площадь одного из круглых концов цилиндра.
Площадь круга равна πr 2 (π × радиус × радиус). π (пи) приблизительно равно 3,14.
Таким образом, площадь конца равна:
3.14 x 2,5 x 2,5 = 19,63 см 2
Объем — это площадь конца, умноженная на длину, и поэтому составляет:
19,63 см 2 x 20 см = 392,70 см 3
Пример 2
Что больше по объему: сфера радиусом 2 см или пирамида с основанием 2,5 см в квадрате и высотой 10 см?
Сначала определим объем сферы .
Объем сферы равен 4/3 × π × радиус 3 .
Таким образом, объем сферы составляет:
.
4 ÷ 3 x 3,14 × 2 × 2 × 2 = 33,51 см 3
Затем определите объем пирамиды .
Объем пирамиды 1/3 × площадь основания × высота.
Площадь основания = длина × ширина = 2,5 см × 2,5 см = 6,25 см 2
Объем, следовательно, равен 1/3 x 6,25 × 10 = 20.83 см 3
Таким образом, сфера больше по объему, чем пирамида.
Расчет объема твердых тел неправильной формы
Точно так же, как вы можете вычислить площадь неправильных двумерных форм, разбив их на правильные, вы можете сделать то же самое для вычисления объема неправильных твердых тел. Просто разделите твердое тело на более мелкие части, пока не получите только твердые тела, с которыми вы сможете легко работать.
Рабочий пример
Вычислите объем водяного цилиндра общей высотой 1 м, диаметром 40 см и полусферической верхней частью.
Сначала вы делите фигуру на две части: цилиндр и полусферу (полусферу).
Объем сферы равен 4/3 × π × радиус 3 . В этом примере радиус составляет 20 см (половина диаметра). Поскольку верхняя часть является полусферической, ее объем будет вдвое меньше полной сферы. Таким образом, объем данного участка формы:
0,5 × 4/3 × π × 203 = 16,755,16 см 3
Объем цилиндра равен площади основания × высоте.Здесь высота цилиндра — это общая высота за вычетом радиуса сферы, которая составляет 1 м — 20 см = 80 см. Площадь цоколя πr 2 .
Таким образом, объем цилиндрического сечения данной формы составляет:
80 × π × 20 × 20 = 100 530,96 см 3
Таким образом, общий объем этого резервуара для воды составляет:
100 530,96 + 16 755,16 = 117 286,12 см 3 .
Это довольно большое число, поэтому вы можете преобразовать его в 117.19 литров путем деления на 1000 (поскольку в литре 1000 см 3 ). Однако вполне правильно выразить его как cm 3 , поскольку задача не требует, чтобы ответ был выражен в какой-либо конкретной форме.
Дополнительная литература по навыкам, которые вам нужны
Понимание геометрии
Часть необходимых навыков Руководство по счету
Эта электронная книга охватывает основы геометрии и рассматривает свойства форм, линий и твердых тел.Эти концепции выстроены в книге с отработанными примерами и возможностями, позволяющими вам практиковать свои новые навыки.
Хотите ли вы освежить в памяти основы или помочь детям в учебе, эта книга для вас.
В заключение…
Используя эти принципы, если необходимо, теперь вы сможете рассчитать объем практически всего в своей жизни, будь то упаковочный ящик, комната или водяной баллон.
Калькулятор объема
.Определение | Формулы
Калькулятор объема рассчитает объем некоторых из наиболее распространенных трехмерных твердых тел. Прежде чем мы перейдем к тому, как рассчитать объем, вы должны знать определение объема. Объем отличается от площади, которая представляет собой объем пространства, занимаемого двухмерной фигурой. Поэтому вы можете быть сбиты с толку относительно того, как найти объем прямоугольника по сравнению с тем, как найти объем коробки. Калькулятор поможет вычислить объем сферы, цилиндра, куба, конуса и прямоугольных тел.
Что такое объем? Определение объема
Объем — это объем пространства, занимаемого объектом или веществом. Как правило, под объемом контейнера понимается его вместимость, а не пространство, которое сам контейнер перемещает. Кубический метр (м 3 ) — это единица измерения объема в системе СИ.
Однако термин том может также относиться ко многим другим вещам, например,
- степень громкости или интенсивность звука (вы можете проверить наш калькулятор шумового загрязнения или калькулятор дБ)
- количество или количество чего-либо (обычно большого количества)
- формальное слово для книги или одной из набора связанных книг.
Единицы объема, таблица пересчета
Популярные единицы объема:
- Метрические единицы объема
- кубических сантиметров (см³)
- кубических метров (м³)
- литров (л, л)
- миллилитров (мл, мл)
- Стандарт США, Великобритания
- жидкая унция (жидкая унция)
- кубических дюймов (у.е.)
- кубических футов
- стаканов
- пинт (пт)
- кварты (кварты)
- галлонов (гал.)
Если вам нужно преобразовать единицы объема, вы можете использовать наш конвертер больших объемов.Еще один полезный инструмент — наш калькулятор граммов в чашки, который может помочь, если вы хотите использовать рецепт еды из другой страны. Обратите внимание, что это не простое преобразование, а переход от веса (граммы) к единице объема (чашки) — поэтому вам нужно знать тип ингредиента (или, точнее, его плотность).
Кроме того, вы можете взглянуть на эту аккуратную таблицу преобразования единиц объема, чтобы узнать коэффициент преобразования в мгновение ока:
| кубических дюймов | кубических футов | кубических ярдов | галлонов жидкости сша | галлонов сухих сша | imp жидких галлонов | баррелей (нефть) | стаканов | жидких унций (Великобритания) | жидких унций (США) | пинт (Великобритания) | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| куб.м | 6.1 10 4 | 35,3 | 1,30 8 | 264,2 | 227 | 220 | 6,29 | 4227 | 3,52 10 4 | 3,38 10 4 | 1760 |
| кубический дециметр | 61.02 | 0,035 | 1,3 10 -3 | 0,264 | 0,227 | 0,22 | 0,006 | 4,23 | 35,2 | 33,8 | 1,76 |
| кубический сантиметр | 0.061 | 3,5 10 -5 | 1,3 10 -6 | 2,64 10 -4 | 2,27 10 -4 | 2,2 10 -4 | 6,29 10 -6 | 4,2 10 -3 | 3,5 10 -2 | 3.34 10 -2 | 1,76 10 3 |
| кубический миллиметр | 6,1 10 -5 | 3,5 10 -8 | 1,31 10 -9 | 2,64 10 -7 | 2,27 10 -7 | 2,2 10 -7 | 6.3 10 -9 | 4,2 10 -6 | 3,5 10 -5 | 3,4 10 -5 | 1,76 10 -6 |
| гектолитров | 6,1 10 3 | 3,53 | 0,13 | 26.4 | 22,7 | 22 | 0,63 | 423 | 3,5 10 3 | 3381 | 176 |
| литра | 61 | 3,5 10 -2 | 1.3 10 -3 | 0,26 | 0,23 | 0,22 | 6,3 10 -3 | 4,2 | 35,2 | 33,8 | 1,76 |
| сантилитров | 0,61 | 3.5 10 -4 | 1,3 10 -5 | 2,6 10 -3 | 2,3 10 -3 | 2,2 10 -3 | 6,3 10 -5 | 4,2 10 -2 | 0,35 | 0,338 | 1.76 10 -2 |
| миллилитры | 6,1 10 -2 | 3,5 10 -5 | 1,3 10 -6 | 2,6 10 -4 | 2,3 10 -4 | 2,2 10 -4 | 6,3 10 -6 | 4.2 10 -3 | 3,5 10 -2 | 3,4 10 -2 | 1,76 10 -3 |
| кубические дюймы | 1 | 5,79 10 -4 | 2,1 10 -5 | 4,3 10 -3 | 3.7 10 -3 | 3,6 10 -3 | 10 -4 | 6,9 10 -2 | 0,58 | 0,55 | 2,9 10 -2 |
| кубических футов | 1728 | 1 | 0.037 | 7,48 | 6,43 | 6,23 | 0,18 | 119,7 | 997 | 958 | 49,8 |
| кубических ярдов | 4,7 10 4 | 27 | 1 | 202 | 173.6 | 168,2 | 4,8 | 3232 | 2,69 10 4 | 2,59 10 4 | 1345 |
| галлонов жидкости сша | 231 | 0,134 | 4,95 10 -3 | 1 | 0.86 | 0,83 | 0,024 | 16 | 133,2 | 128 | 6,7 |
| сухих галлонов сша | 268,8 | 0,156 | 5,76 10 -3 | 1.16 | 1 | 0,97 | 0,028 | 18,62 | 155 | 148,9 | 7,75 |
| imp жидкие галлоны | 277,4 | 0,16 | 5,9 10 -3 | 1.2 | 1,03 | 1 | 0,029 | 19,2 | 160 | 153,7 | 8 |
| баррелей (нефть) | 9702 | 5,61 | 0,21 | 42 | 36.1 | 35 | 1 | 672 | 5596 | 5376 | 279,8 |
| чашки | 14,4 | 8,4 10 -3 | 3,1 10 -4 | 6.2 10 -2 | 5,4 10 -2 | 5,2 10 -2 | 1,5 10 -3 | 1 | 8,3 | 8 | 0,4 |
| жидких унций (Великобритания) | 1,73 | 10-3 | 3.7 10 -5 | 7,5 10 -3 | 6,45 10 -3 | 6,25 10 -3 | 1,79 10 -4 | 0,12 | 1 | 0,96 | 5 10 -2 |
| жидких унций (США) | 1.8 | 10 -3 | 3,87 10 -5 | 7,8 10 -3 | 6,7 10 -3 | 6,5 10 -3 | 1,89 10 -4 | 0,13 | 1,04 | 1 | 0.052 |
| пинты (Великобритания) | 34,7 | 0,02 | 7,4 10 -4 | 0,15 | 0,129 | 0,125 | 3,57 10 3 | 2,4 | 20 | 19.2 | 1 |
Как рассчитать объем? Формулы объема
На этот вопрос нет однозначного ответа, так как он зависит от формы рассматриваемого объекта. Вот формулы для некоторых наиболее распространенных форм:
Куб =
с³, где с — длина стороны.Сфера =
(4/3) πr³, где r — радиус.Цилиндр =
πr²h, где r — радиус, а h — высота.Конус =
(1/3) πr²h, где r — радиус, а h — высота.Прямоугольное тело (объем ящика) =
lwh, где l — длина, w — ширина и h — высота (примером такой формы может служить простой бассейн).Пирамида =
(1/3) Ач, где A — площадь основания, а h — высота. Для пирамиды с правильным основанием также можно использовать другое уравнение: Пирамида =(n / 12) * h * длина_сокры ² * кроватка (π / n), где n — количество сторон основания для правильный многоугольник.Призма =
πAh, где A — площадь основания, а h — высота. Для прямоугольной призмы уравнение можно легко вывести, как и для правой прямоугольной призмы, которая, по-видимому, имеет ту же форму, что и прямоугольник.
| Форма | Имя | Формула |
|---|---|---|
| Куб | В = с³ | |
| Призма прямоугольная правая (прямоугольная, прямоугольная) | V = lwh | |
| Призма или цилиндр | В = Ач | |
| Пирамида или конус | В = Ач / 3 | |
| Сфера | V = 4πr³ / 3 |
Калькулятор объема и инструменты, предназначенные для определенных форм
Мы решили сделать из этого калькулятора объема простой инструмент, охватывающий пять самых популярных трехмерных фигур.Однако не все уравнения объема и формы могут быть реализованы здесь, так как это сделает калькулятор перегруженным и не интуитивно понятным. Так что, если вы ищете конкретную форму, ознакомьтесь с калькуляторами, посвященными объемам выбранных форм:
Калькулятор объема — как использовать
Давайте посмотрим на примере использования этого калькулятора объема:
Выберите тип 3D-формы . Если вы не можете найти форму, объем которой хотите рассчитать, выберите другие специальные специальные калькуляторы (ссылки вы найдете выше).В этом примере предположим, что вы хотите рассчитать объем цилиндра.
Выберите правую часть калькулятора объема . В нашем случае это деталь под названием Объем цилиндра .
Введите данные в соответствующие поля . Наш цилиндр имеет радиус 1 фут и высоту 3 фута. Вы можете изменить единицы измерения простым щелчком по названию единицы.
Вот и все! Объем выбранной формы отображается .В нашем случае это 9,42478 куб. Футов
Если вы хотите проверить, сколько это в баррелях США, просто нажмите на название единицы и выберите бочки из раскрывающегося списка. Наш цилиндр вмещает ~ 2,24 баррелей масла.
Измерение объема твердых тел, жидкостей и газов
Как найти объем объектов с разным состоянием материи?
- Цельный
Для обычных трехмерных объектов вы можете легко вычислить объем, измерив его размеры и применив соответствующее уравнение объема.Если это неправильная форма, вы можете попробовать сделать то же самое, что заставило Архимеда выкрикнуть знаменитое слово * Эврика *! Вероятно, вы слышали эту историю — Архимеда попросили выяснить, сделана ли корона Иеро из чистого золота или просто позолочена, но не сгибая и не разрушая ее. Идея пришла ему в голову, когда он принимал ванну — войдя в ванну, он заметил, что уровень воды поднялся. Из этого наблюдения он пришел к выводу, что объем вытесненной воды должен быть равен объему той части его тела, которую он погрузил в воду.Зная объем необычного объекта и его вес, он мог вычислить плотность и сравнить ее с плотностью чистого золота. Легенда гласит, что Архимед был так взволнован этим открытием, что выскочил из ванны и побежал голым по улицам Сиракуз.
Итак, если вы хотите измерить объем необычного объекта, просто следуйте по стопам Архимеда (хотя вы можете опустить часть «голая гонка»):
Возьмите емкость больше, чем объект, объем которого вы хотите измерить .Это может быть ведро, мерный стаканчик, химический стакан или мерный цилиндр. На нем должна быть шкала.
Налейте воду в емкость и снимите показания объема.
Поместите объект внутрь . Он должен быть полностью погружен для измерения всего объема объекта. Прочтите том. Этот метод не сработает, если ваш объект растворяется в воде.
Разница между измерениями — это объем нашего объекта.
Эти измерения необходимы для расчета выталкивающей силы, основанной на принципе Архимеда.
- Жидкость
Обычно измерить объем жидкости довольно просто — все, что вам нужно, — это какой-нибудь мерный сосуд с градуировкой. Выберите тот, который соответствует вашим потребностям: необходимо учитывать количество жидкости и степень точности. Емкости, используемые для выпечки торта (посмотрите отличный калькулятор для рецепта блинов), будут отличаться от тех, что используются в химии (например.грамм. в расчетах молярной концентрации) будет отличаться от тех, которые используются в медицинских целях (например, доза лекарства).
- Газ
Мы должны использовать более сложные методы для измерения объема газа. Вы должны помнить, что на объем газа влияют температура и давление, и что газы расширяются, чтобы заполнить любой контейнер, в который они помещены. Можно попробовать измерить это:
Надуйте баллон газом, который вы хотите измерить (например,г., с гелием, чтобы поднять вас в воздух). Затем можно воспользоваться методом Архимеда — опустить баллон в ведро с водой и проверить разницу объемов. Вы найдете подробные инструкции на странице wikihow.
Проверьте показатели, связанные с объемом ваших легких, с помощью прибора под названием спирометр .
В химии, газовый шприц используется для ввода или отбора объема газа из закрытой системы . Эту лабораторную посуду также можно использовать для измерения объема газа, выделяющегося в результате химической реакции.
Или рассчитать :
Найдите объем газа, , учитывая его плотность и массу . Используйте простое уравнение объема
V = m / d.Рассчитайте объем сжатого газа в баллоне, используя уравнение идеального газа.
Как найти объем * прямоугольника * по сравнению с объемом * коробки *
Вы не можете рассчитать объем прямоугольника , объем круга или объем квадрата, потому что это двухмерные геометрические фигуры.Таким образом, прямоугольник не имеет объема (но имеет площадь). Вероятно, вы ищете объем прямоугольного кубоида (или, говоря более общим языком, вы хотите найти объем коробки), который представляет собой трехмерный объект.
Чтобы найти объем коробки, просто умножьте длину, ширину и высоту — и готово! Например, если размер коробки 5х7х2 см, то объем коробки составляет 70 кубических сантиметров.
Для размеров, которые представляют собой относительно небольшие целые числа, легко вычислить объем вручную.Для больших или десятичных чисел использование калькулятора объема очень эффективно.
В реальной жизни есть много приложений, в которых может пригодиться калькулятор объема. Один из таких примеров — строительство дорог или тротуаров, где должны быть построены бетонные плиты. Как правило, бетонные плиты представляют собой твердые тела прямоугольной формы, поэтому можно использовать калькулятор бетона, который является приложением калькулятора объема.
Также формулы объема могут быть полезны, если вы увлеченный садовник или просто счастливый обладатель дома с двором.Ознакомьтесь с нашими замечательными инструментами, такими как:
Более того, вы можете встретить объем на кухне или в ванной: у любой жидкости, которую мы пьем (например, воды в бутылках), а также косметических товаров или зубной пасты, на упаковке продукта указан объем (в миллилитрах / литрах или жидких унциях). / галлоны).
Еще одно родственное приложение, хотя и немного другое, — это концепция площади поверхности. Предположим, что весь фасад здания должен быть окрашен. Чтобы знать, сколько нужно приобрести краски, необходимо рассчитать площадь здания.Удобный в использовании калькулятор площади рассчитает это за вас.
FAQ
Как найти объем?
Формула объема зависит от формы объекта . Одной из самых популярных форм является прямоугольная призма, также известная как коробка, где вы можете просто умножить длину на ширину на высоту , чтобы найти ее объем. Другой распространенной формой является цилиндр — чтобы найти его объем, умножьте высоту цилиндра на площадь его основания (π ⨉ r 2 ).Для других трехмерных фигур проверьте Калькулятор объема Omni.
Как измерить объем?
Измерение объема зависит от состояния вещества вашего объекта. Для жидкостей вы можете использовать мерный цилиндр или бюретку для измерений в химической лаборатории, или мерную чашку и ложку для повседневных целей. Что касается газов, чтобы приблизительно измерить объем, вы можете надуть баллон и использовать его для вытеснения воды в мерном цилиндре. Аналогичный метод работает для твердых тел — поместите объект в градуированный контейнер и измерьте изменение показаний.
Объем — квадрат или куб?
Объем — это «куб» , так как это трехмерная мера. Площадь — это «квадратное» значение, поскольку площадь фигуры охватывает два измерения. Вы можете вспомнить, что объем представляет собой кубическое значение, вспомнив несколько названий единиц объема, например, кубических метров , кубических футов или кубических ярдов .
Как рассчитать объем?
В зависимости от формы объекта вы можете использовать разные формулы для расчета объема:
- Объем куба = сторона 3 .
- Кубоид (прямоугольная коробка) объем = длина ⨉ ширина ⨉ высота
- Объем сферы = (4/3) ⨉ π ⨉ радиус 3
- Объем цилиндра = π ⨉ радиус 2 ⨉ высота
- Объем конуса = (1/3) ⨉ π ⨉ радиус 2 ⨉ высота
- Объем пирамиды = (1/3) площадь основания ⨉ высота
В чем измеряется объем?
Кубический метр — единица объема в системе СИ.Однако, поскольку это довольно непрактично, чаще всего вы можете встретить объем, выраженный в:
- Кубические сантиметры
- Кубические дюймы
- Миллилитров
- литров
- галлонов
Как найти объем жидкости?
Градуированные цилиндры и Колбы Эрленмейера подойдут, если вам нужно приблизительно измерить объем жидкости. Для более точных измерений нужно использовать мерную пипетку и бюретку.Однако, если вы печете торт или готовите вкусное блюдо и в рецепте используются единицы объема, вы можете просто использовать мерный стакан, стакан или ложку.
Что такое единица СИ для объема?
Кубический метр (м 3 ) — это единица измерения объема в системе СИ. Он образован от основной единицы длины в системе СИ — метра. Хотя кубический метр является основной единицей СИ, чаще используются другие единицы: для метрической системы популярны миллилитры, литры или кубические сантиметры, а для имперской системы вы можете найти объем, выраженный в пинтах, галлонах, кубических дюймах и т. Д. кубические футы или кубические ярды.
Объем интенсивный или обширный?
Объем — это обширное свойство , такое же, как количество вещества, массы, энергии или энтропии. Обширное свойство — это мера, которая зависит от количества вещества . Посмотрите на этот пример: стакан, бочка и бассейн, полный воды, имеют разные объем и массу ( расширенных свойств ), но вода в этих трех контейнерах будет иметь одинаковую плотность, показатель преломления и вязкость ( интенсивные свойства ). ).
В чем разница между площадью поверхности и объемом?
Объем — это трехмерная величина , а площадь поверхности — двумерная . Объем сообщает нам о кубическом пространстве, которое занимает объект, а площадь поверхности — это сумма всех областей, образующих трехмерную форму. Возьмем, например, картонную коробку 📦:
- Объем — это объем места, занимаемый коробкой, просто пространство, доступное внутри коробки
- Площадь поверхности — это пространство , занимаемое сторонами коробки, вычисленное при покраске сторон или упаковке коробки в бумагу.
Как найти объем объекта неправильной формы?
Вы можете использовать метод смещения жидкости для твердых объектов неправильной формы:
- Заполните емкость водой и отметьте уровень воды.
- Бросьте ваш объект внутрь и снова отметьте уровень. Убедитесь, что ваш объект не растворяется в воде.
- Для масштабированных контейнеров вы можете всего вычесть исходного объема из нового объема. И все, поздравляю!
Но если на вашем оригинальном контейнере нет весов:
- Вынуть предмет.
- Заполните вашу емкость водой до второй отметки, налейте этой воды в мерный цилиндр / другую мерную емкость.
- Повторите шаг 6 для другого отмеченного уровня и вычтите объемы.
- Pat себе на спину — вы нашли объем объекта неправильной формы!
Что измеряет объем?
Объем измеряет объем пространства, занимаемого объектом в трех измерениях .Еще один близкий термин — вместимость, то есть объем внутреннего пространства объекта. Другими словами, вместимость описывает, сколько контейнер может вместить (воды, газа и т. Д.).
Каков объем Земли?
Объем Земли приблизительно равен 1,08321 × 10 12 км 3 ( 1,08 квадриллион кубических километров ), или 2,59876 × 10 11 кубических миль ( 259 триллионов кубических миль ). Вы можете получить этот результат, используя формулу объема сферы (4/3) ⨉ π ⨉ radius 3 и предполагая, что средний радиус Земли составляет 6371 километр (3958.76 миль).
Как рассчитать отношение площади поверхности к объему?
Чтобы вычислить отношение площади поверхности к объему SA: V, вы просто разделите площадь поверхности на объем . Для некоторых выбранных форм:
- Соотношение SA: V для куба = (сторона 6 ⨉ 2 ) / (сторона 3 ) = 6 / сторона
- Соотношение SA: V для сферы = (4 ⨉ π ⨉ радиус 2 ) / ((4/3) ⨉ π ⨉ радиус 3 ) = 3 / радиус
- Соотношение SA: V для цилиндра = (2 ⨉ π ⨉ радиус 2 + 2 ⨉ π ⨉ радиус ⨉ высота) / (π ⨉ радиус 2 ⨉ высота) = 2 ⨉ (радиус + высота) / ( радиус ⨉ высота)
Как рассчитать объем
Расчет объема
Объем измеряется в кубах (или кубических единицах).
Сколько кубиков в этой прямоугольной призме (кубоиде)?
Мы можем считать кубики, хотя быстрее вычислить длину, ширину и высоту и использовать умножение. Прямоугольная призма выше имеет объем 48 кубических единиц.
Объем прямоугольной призмы = длина x ширина x высота
Примеры расчета площади прямоугольника
Нам нужно сделать два умножения, чтобы вычислить объем. Мы вычисляем площадь одной грани (или стороны) и умножаем ее на ее высоту.Примеры ниже показывают, как это можно сделать тремя способами.
Обратите внимание, как мы получаем один и тот же ответ независимо от того, какой стороной мы ищем область.
Когда ваш ребенок начинает работать с площадью и периметром, он или она обычно работает с двумя измерениями — квадратами, прямоугольниками, треугольниками и т. Д., Которые показаны на бумаге как плоские — нет глубины или третьего измерения. Работа с объемом действительно включает 3 измерения. Убедитесь, что ваш ребенок знает об этом и не думает о кубах и других трехмерных фигурах, показанных на бумаге, как о еще одной «фигуре на странице».«Покажите им настоящие коробки и покажите, как их можно нарисовать (или изобразить) на двухмерном листе бумаги. Другими словами, убедитесь, что существует связь между тем, что на бумаге, и тем, что она представляет в реальном мире.
Убедитесь, что вашего ребенка не смущает использование громкости , когда речь идет о громкости.
Единицы измерения объема
Есть очень большие различия между единицами измерения объема. Например, в 1 метре 100 сантиметров, а в кубическом метре 1000000 (да, 1 миллион) кубических сантиметров.
Почему большая разница? Потому что по объему у нас есть не только длина; у нас есть длина, ширина и высота. Пример кубика сахара ниже показывает это.
Сколько сахара? 1 м 3 или 1000000 см 3
Подумайте о заполнении очень большой коробки (шириной 1 метр, длиной 1 метр и высотой 1 метр) кубиками сахара (с каждой стороной 1 сантиметр).
| Шаг 1: один ряд вдоль дна коробки — , что составляет 100 кубиков сахара | |
| Шаг 2: закройте оставшуюся часть основания коробки — , что даст в общей сложности 100 рядов с 100 кубиков сахара в каждом.100 x 100 = 10000 сахара кубика на дне большой коробки. | |
| Шаг 3: Повторите это 99 раз, пока не получите слоев по 10 000 кубов, уложенных стопкой в 100 слоев. 10 000 x 100 = 1 000 000 кубиков сахара |
1000000 см 3 в 1 м 3 — будьте осторожны, чтобы не было слишком много сахара!
Есть и другие единицы измерения объема; кубические дюймы, кубические футы, кубические ярды — все это единицы измерения объема.Миллилитры, литры, галлоны также используются, особенно при измерении жидкостей.
| Не забывайте крошечный 3 |
| Пишем кубические размеры с помощью маленькой 3 рядом с единицей. Мы пишем mm 3 , cm 3 , m 3 , km 3 , cm 3 Мы можем сказать «85 сантиметров в кубе» или «85 кубических сантиметров» |
Примеры расчета объема прямоугольных призм
| Объем = длина x ширина x высота Объем = 12 см x 8 см x 6 см = 576 см 3 | |
| Объем = длина x ширина x высота Объем = 20 м x 2 м x 2 м = 80 м 3 | |
| Объем = длина x ширина x высота Объем = 10 м x 4 м x 5 м = 200 м 3 |
Объем цилиндра
Для вычисления объема цилиндра нужно умножить площадь основания на высоту цилиндра.Основание цилиндра круглое, а формула для вычисления площади круга: площадь круга = πr 2 . Здесь больше о площади круга.
| Объем = Площадь основания x Высота Объем = πr 2 x h Объем = πr 2 h |
Примечание: в приведенных ниже примерах мы будем использовать 3,14 как приблизительное значение для π (Pi).
Пример расчета объема цилиндра
| Размеры указаны в см. | Объем = πr 2 ч Объем = 3,14 x 3 x 3 x 8 Объем = 226,08 см 3 |
Объем конуса
Объем конуса равен одной трети объема цилиндра с соответствующей высотой и площадью основания. Это дает формулу для объема конуса, как показано ниже.
| Объем = 1/3 πr 2 ч |
Пример расчета объема конуса
| Размеры указаны в см. | Объем = 1/3 πr 2 ч Объем = 1/3 x 3,14 x 2 x 2 x 7 Объем = 29,31 см 3 |
Объем сферы
Формула объема шара приведена ниже.
| Объем = 4/3 πr 3 |
Пример расчета объема сферы
| Размеры указаны в см. | Объем = 4/3 πr 3 Объем = 4/3 x 3,14 x 4 x 4 x 4 Объем = 267,95 см 3 |
Рабочие листы для печати
Используйте таблицу ниже, чтобы попрактиковаться в вычислении объемов.
Здесь вы получите другие рабочие листы геометрии по периметру, площади и т. Д.
Как рассчитать площадь комнаты
Когда вас попросят измерить квадратный фут / метр, вам нужно будет вычислить площадь.
Полы
Для квадратной или прямоугольной комнаты вам нужно сначала измерить длину, а затем ширину комнаты.
Затем умножьте длину и ширину. Длина x Ширина = Площадь.
Итак, если ваша комната имеет размеры 11 футов в ширину и 15 футов в длину, ваша общая площадь будет 165 квадратных футов. Это измерение понадобится вам при оценке количества раствора для плитки, раствора и герметика, которые вы будете использовать для своего проекта.
Как правило, вы можете добавить коэффициент потерь 10%: просто умножьте свою площадь на 1.1, а затем округлить в большую сторону. Итак, если ваша общая площадь составляет 165 квадратных футов, вам нужно будет заказать достаточно раствора для плитки и раствора для 182 квадратных футов.
Если ваша комната не идеально квадратная (например, в форме буквы «L»), вам нужно будет разделить комнату на две части, чтобы вычислить общую площадь.
Измерьте высоту и длину каждого прямоугольника, вычислите общую площадь каждого прямоугольника и затем сложите итоги. Не забудьте добавить 10% -ный коэффициент потерь: просто умножьте свою площадь на 1.1, а затем округлить в большую сторону.
Если ваша комната имеет диагональную форму или угол, вам нужно будет разделить комнату на две части, чтобы рассчитать общую площадь.
Сначала измерьте длину и ширину прямоугольника. Затем вычислите общую площадь прямоугольника.
Затем измерьте ширину и высоту основания треугольника (длина сверху вниз). Затем разделите основание на 2 и умножьте это число на высоту. (½ основания) x высота = площадь.
Наконец, сложите области прямоугольника и треугольника.Не забудьте добавить 10% -ный коэффициент потерь: просто умножьте свою площадь на 1,1, а затем округлите в большую сторону.
Стены
Сначала вам нужно измерить высоту и длину стены.
Затем умножьте высоту и длину. Высота x Длина = Площадь.
Итак, если ваша стена имеет высоту 4 фута и длину 9 футов, ваша общая площадь будет 36 квадратных футов. Это измерение понадобится вам при оценке количества раствора для плитки, раствора и герметика, которые вы будете использовать для своего проекта.
Как правило, вы можете добавить коэффициент потерь 10%: просто умножьте свою площадь на 1,1 и затем округлите в большую сторону. Итак, если ваша общая площадь составляет 36 квадратных футов, вам нужно будет заказать достаточно раствора для плитки и раствора для 40 квадратных футов.
ОБЪЕМ ВАННЫ:
Если у вас несколько стен, например, в случае окантовки ванны, это просто. Начните с того же метода расчета площади одной стены. Просто измерьте высоту и длину каждой стены, вычислите общую площадь каждой стены, сложите, а затем сложите общие площади.Не забудьте добавить 10% -ный коэффициент потерь: просто умножьте вашу площадь на 1,1, а затем округлите в большую сторону.
Расчет объема помещения с наклонным потолком
Я получаю общий объем около 16 654 кубических футов.
См. Мою схему:
Надеюсь, это достаточно разборчиво.
Обычно мы кладем пол на выбранную нами координатную плоскость. Так как верхний правый угол — единственный прямой угол на краю комнаты, я выбрал его в качестве начала координат.
Затем мы находим координаты всех углов комнаты и выражаем высоту потолка в виде плоскости; тогда объем комнаты представляет собой двойной интеграл над планом этажа этой плоскости.
Двойной интеграл наиболее прост при разбиении на трапециевидные области; Я не мог понять, как использовать менее 4 (помечены на графике $ A, B, C, D $).
Нам нужно использовать теорему Пифагора, чтобы найти координаты двух точек: низ области $ B $ и низ области $ C $.Используемые уравнения находятся справа от схемы.
Мы решаем плоскость, описывающую высоту вашего потолка, используя общую формулу для плоскости, $ f (x, y) = ax + by + c $ и вставляя три точки, высоты которых мы знаем, чтобы найти $ (a, б, в) $. Если мы используем три точки, которые вы нам сказали: $ (0,0,0), (-25, -35,5,11), (-11, -38,15,10) $, мы получим $ (a, b, c) \ приблизительно (-. {- 25} \ intop _ {-.{-17} f (x, y) dydx $$
Я подключил эти интегралы в Wolfram Alpha (например), чтобы получить окончательные приближения, и добавил их.
РЕДАКТИРОВАТЬ:
Фактически, с некоторой осторожностью мы можем заставить WolframAlpha дать нам общий ответ в терминах $ (a, b, c) $, которые описывают вашу крышу, используя $ \ max $ и $ \ min $ для описания нижняя граница (иначе запрос будет слишком длинным для сайта):
$$ V (a, b, c) = — 12781.8a-13824.9b + 820.356c $$
Итак, как только вы определитесь, какие высоты использовать для описания вашей крыши, решите для $ (a, b, c) $ и подключите его к этому простому уравнению.
Мы не можем найти эту страницу
(* {{l10n_strings.REQUIRED_FIELD}})
{{l10n_strings.CREATE_NEW_COLLECTION}} *
{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}
{{l10n_strings.COLLECTION_DESCRIPTION}}
{{addToCollection.description.length}} / 500
{{l10n_strings.TAGS}}
{{$ item}}
{{l10n_strings.PRODUCTS}}
{{l10n_strings.DRAG_TEXT}}
{{l10n_strings.DRAG_TEXT_HELP}}
{{l10n_strings.ЯЗЫК}}
{{$ select.selected.display}}
{{article.content_lang.display}}
{{l10n_strings.AUTHOR}}
{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}
{{$ select.selected.display}}
{{l10n_strings.CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}}
{{l10n_strings.CREATE_A_COLLECTION_ERROR}}
.

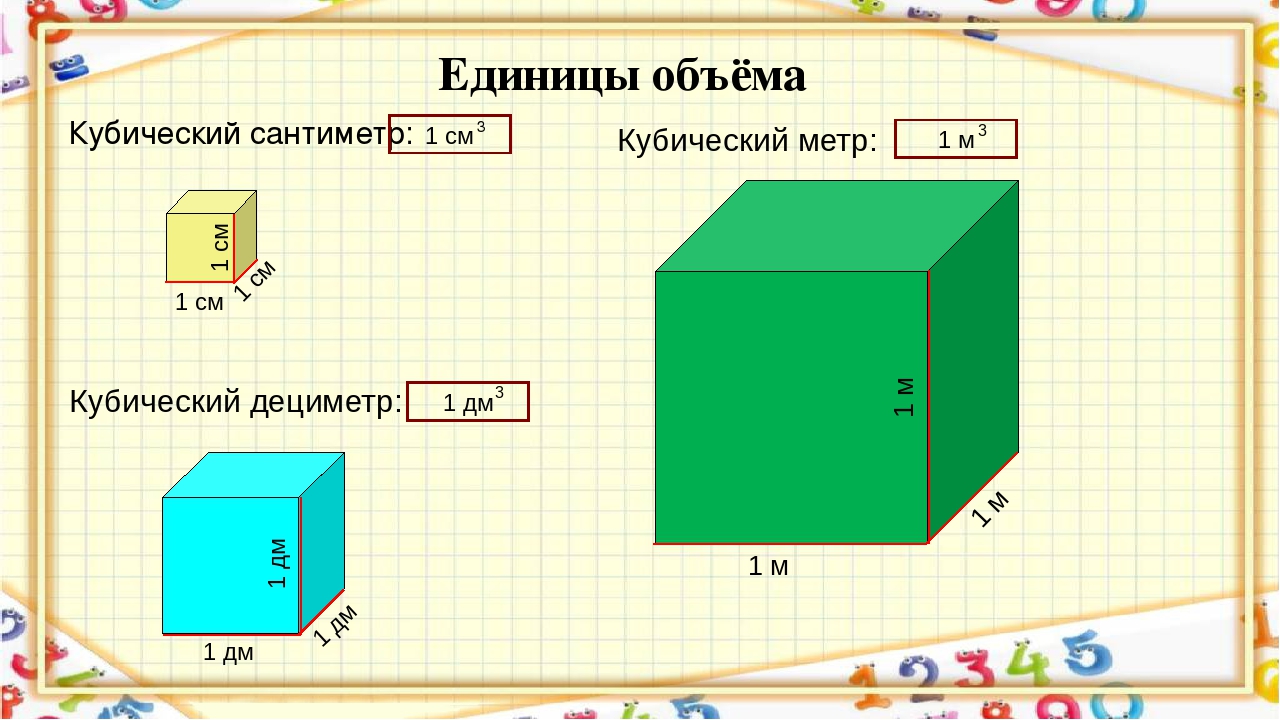 м.
м. м. После округления получаем 1,2 кв. м.
м. После округления получаем 1,2 кв. м.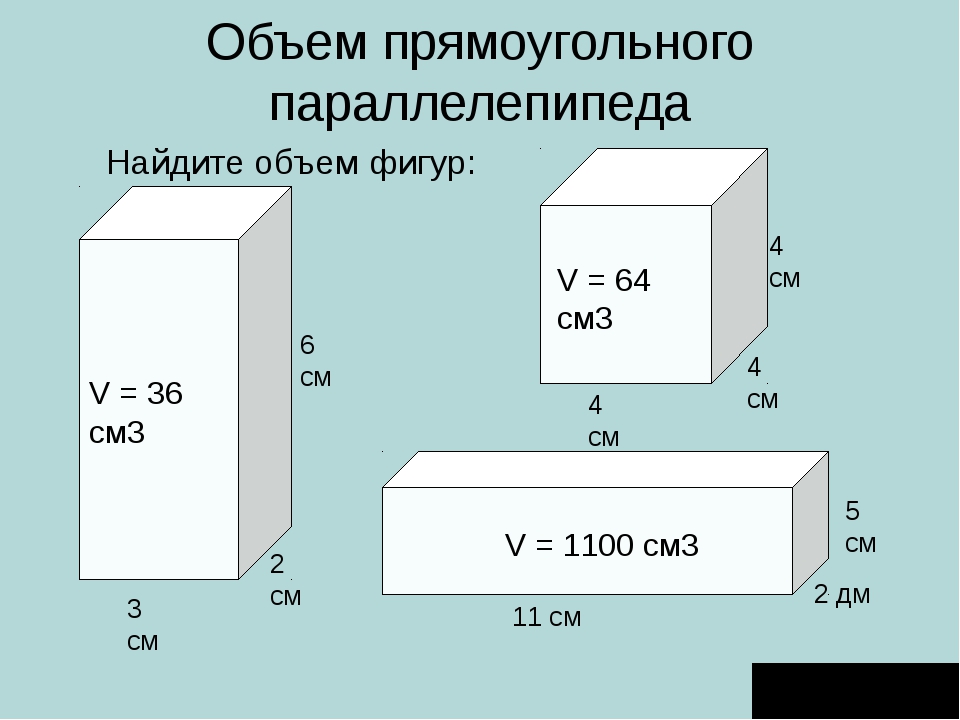
 Количественные характеристики, описывающие пространство, как правило, требуют проведения некоторых измерений и несложных вычислений.
Количественные характеристики, описывающие пространство, как правило, требуют проведения некоторых измерений и несложных вычислений.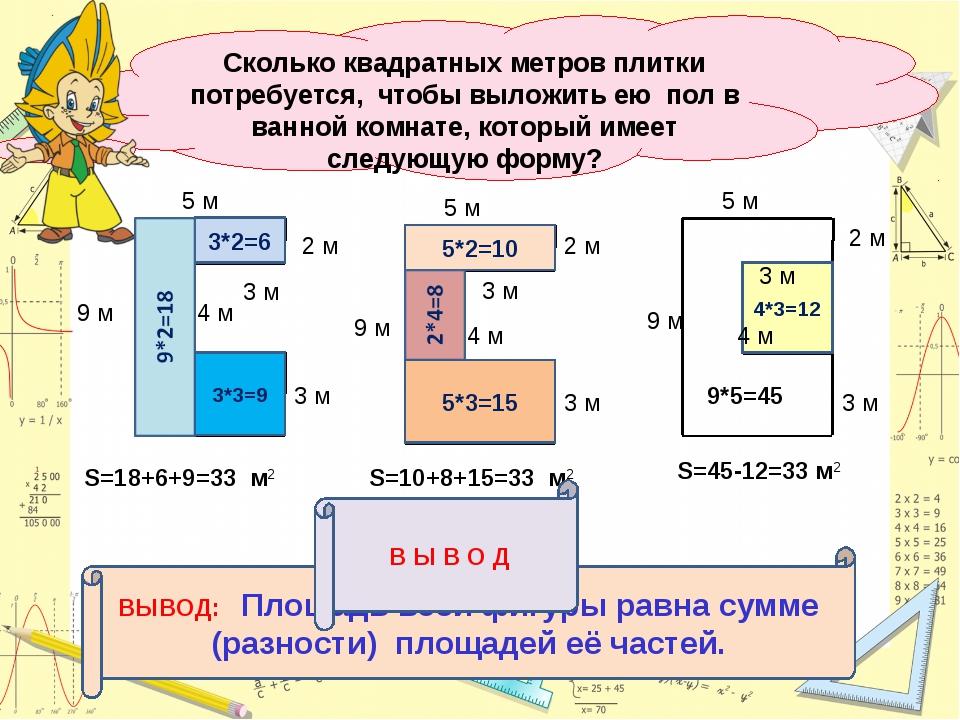 Так называемый строительный объем наземной части здания с чердаком можно вычислить, умножив площадь горизонтального сечения по внешним обводам на уровне нижнего этажа. Измерьте полную высоту здания от уровня чистого пола до верхней части утеплителя чердачного перекрытия. Перемножьте оба показателя.
Так называемый строительный объем наземной части здания с чердаком можно вычислить, умножив площадь горизонтального сечения по внешним обводам на уровне нижнего этажа. Измерьте полную высоту здания от уровня чистого пола до верхней части утеплителя чердачного перекрытия. Перемножьте оба показателя.
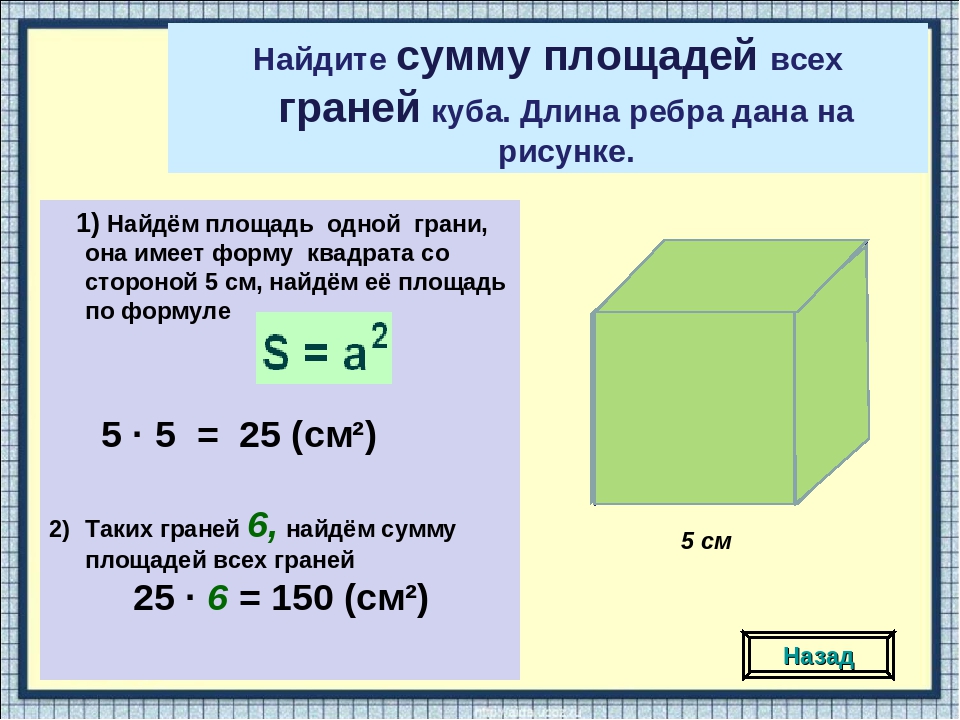 Сложите полученные значения, суммируя площадь. Умножьте сумму на высоту помещения. Измерения необходимо проводить в одних и тех же единицах, например, в метрах.
Сложите полученные значения, суммируя площадь. Умножьте сумму на высоту помещения. Измерения необходимо проводить в одних и тех же единицах, например, в метрах.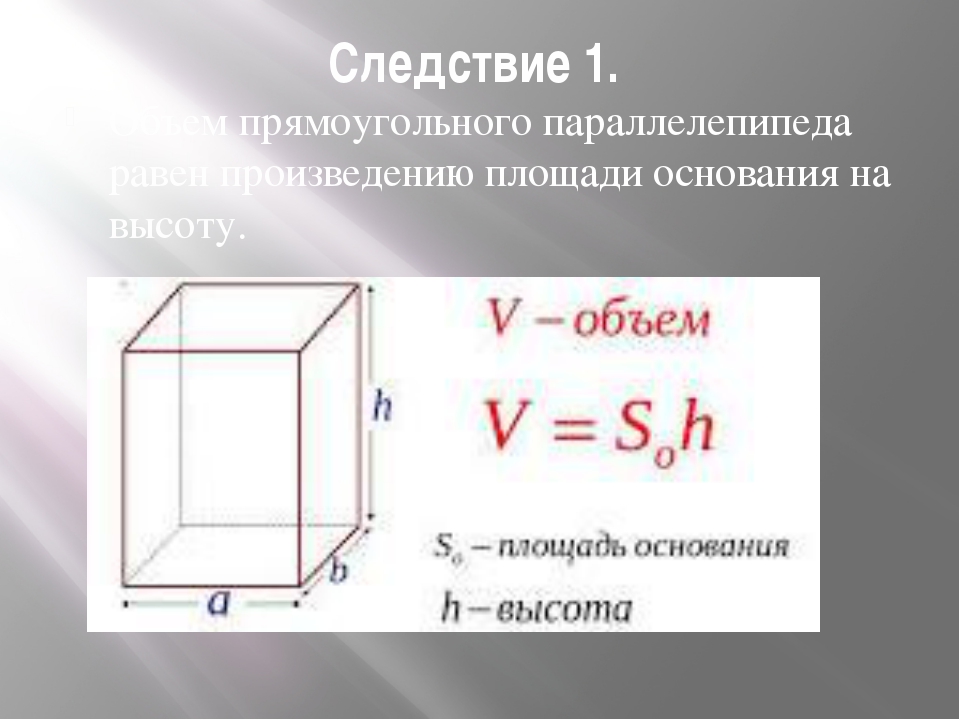
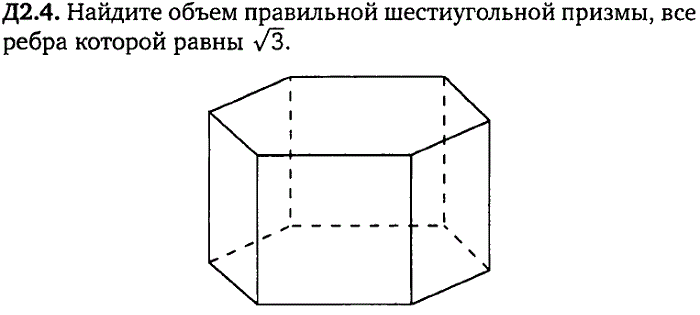 com
com
 Она расскажет обо всех объемных нюансах, что вас могут интересовать, дабы правильно все просчитать.
Она расскажет обо всех объемных нюансах, что вас могут интересовать, дабы правильно все просчитать.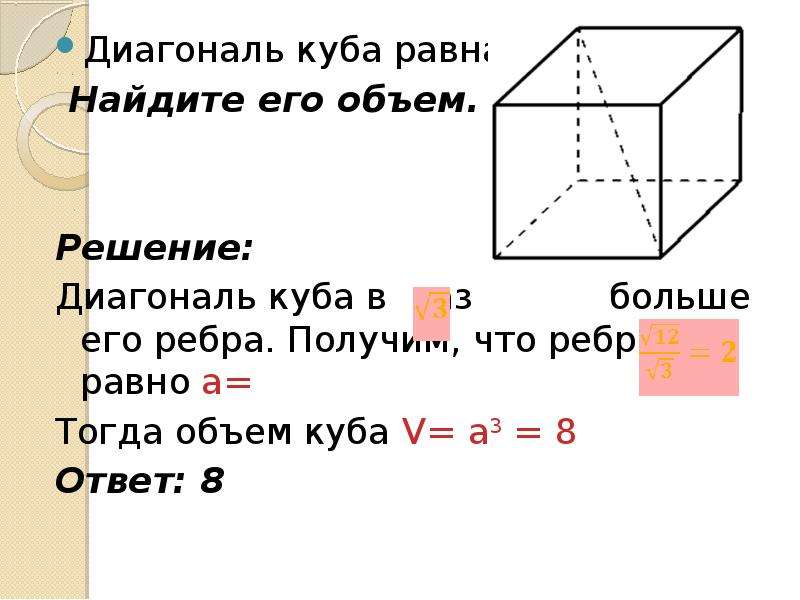
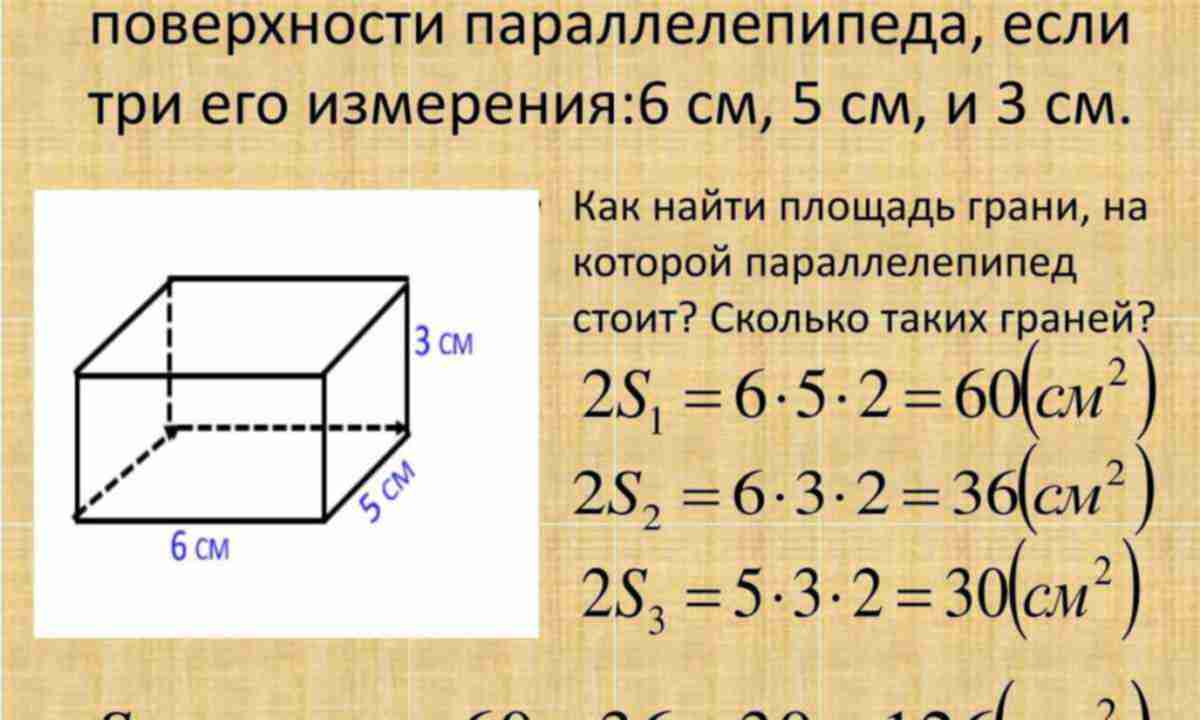
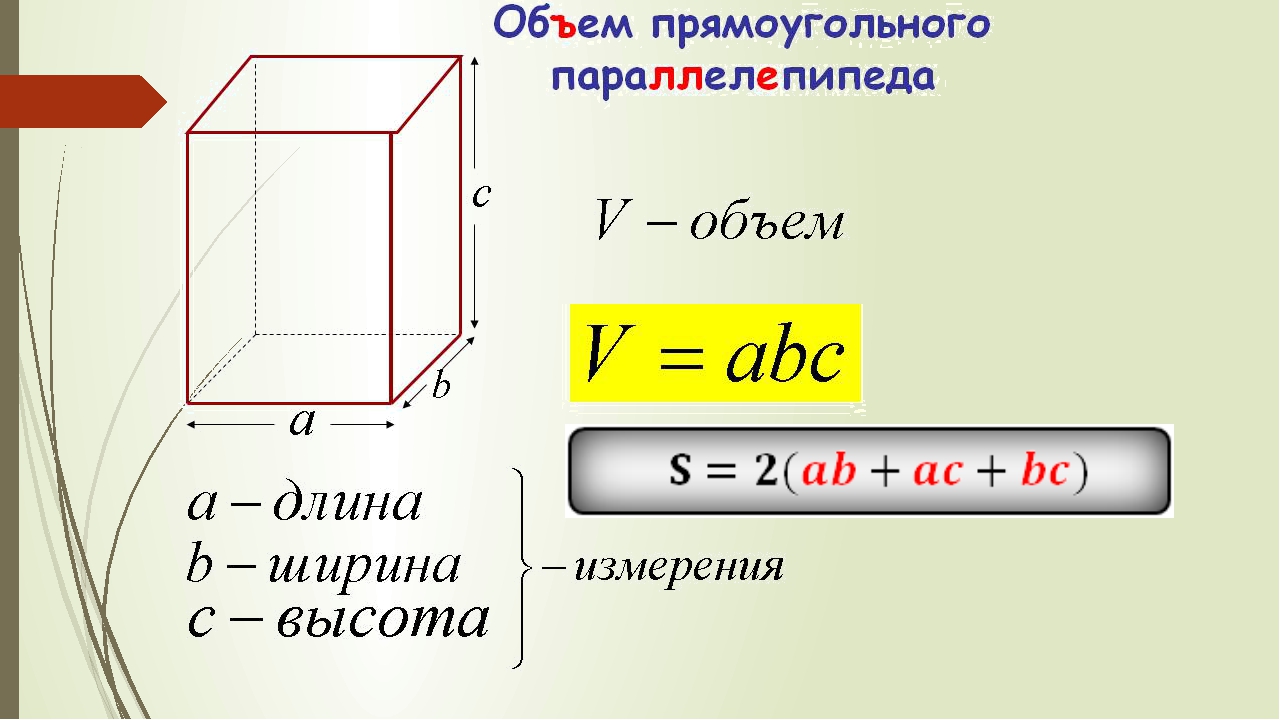 Кстати, не стоит округлять полученные размеры. Желательно учитывать даже миллиметровые показатели. Хотя при просчете обоев или краски все равно идет округление с последующим наброском дополнительных материалов.
Кстати, не стоит округлять полученные размеры. Желательно учитывать даже миллиметровые показатели. Хотя при просчете обоев или краски все равно идет округление с последующим наброском дополнительных материалов.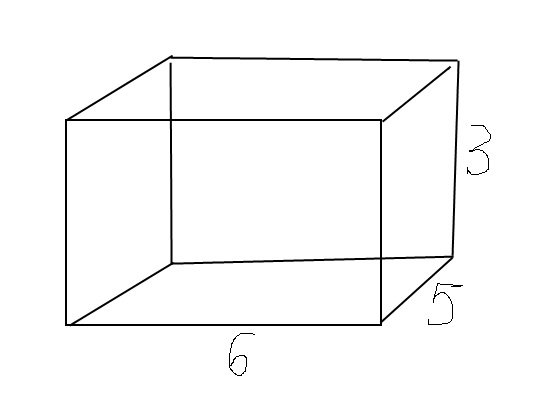 Например, прямоугольная комната имеет так называемый «аппендикс».
Например, прямоугольная комната имеет так называемый «аппендикс».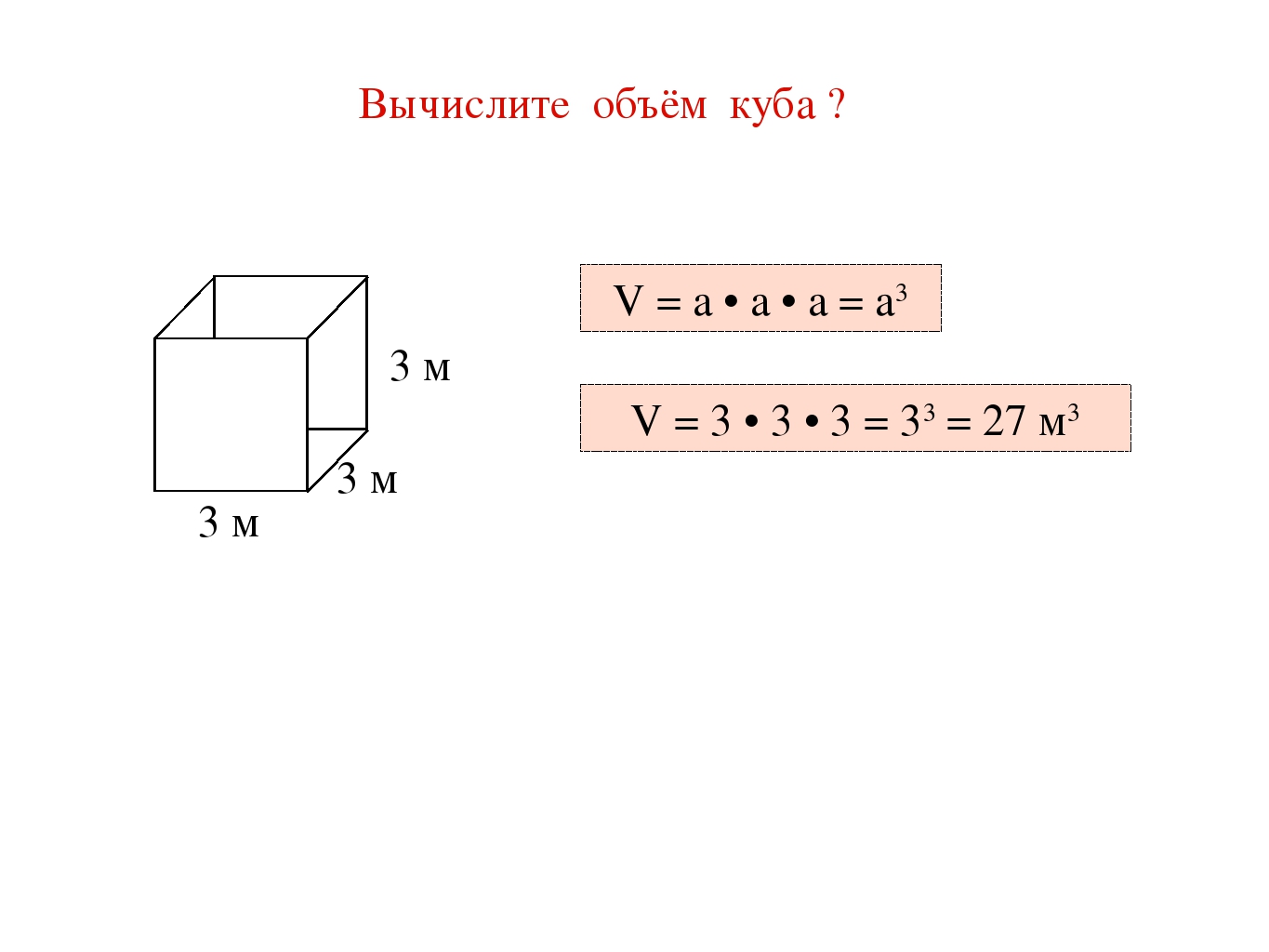 Но мы рассмотрим самые распространенные варианты.
Но мы рассмотрим самые распространенные варианты. Для этого вдоль малой стены мы натянули нить, а на средине отрезка и нашли центральную точку. Радиус у нас равен 1,5 м.
Для этого вдоль малой стены мы натянули нить, а на средине отрезка и нашли центральную точку. Радиус у нас равен 1,5 м.