Площадь и объем: Формулы площадей и объемов геометрических фигур

Объем, Площадь поверхности, формулы объема

Стандартное обозначение объема есть V.
Этим мы измеряем количество (наример, воды), которая может заполнить фигуру.
Только пространственные фигуры имеют объем. Например, треугольники, квадраты не имеют объема, но шар имеет объем (потому что он может быть заполнен чем-то, например водой).

Прямоугольный параллелепипед

Прямоугольный параллелепипед это фигура, все стороны которой — прямоугольники.
Если длины стороны прямоугольника в основе есть a и
b и третье ребро c

тогда формула объема есть:

$V = a \cdot b \cdot c$

Площадь поверхности:

S = $2(a \cdot b + a \cdot c + b \cdot c)$

Куб

Куб есть параллелепипедом, все ребра (стороны) которого равны.

Если длина стороны куба равна a, тогда формула объема:

$V = a.a.a = a^3$

Площадь поверхности:

$S = 6a \cdot a = 6a^2$

Параллелепипед

Параллелепипед это фигура, все стороны которой — параллелограммы.
Если площадь основы равна S и высота параллелепипеда равны h,
то формула объема есть:

$V = S \cdot h$

Пирамида

Пирамида это фигура, основа которой есть треугольник, параллелограмм (квадрат, прямоугольник) или другая фигура с n-углами и треугольными сторонами.
Если площадь основы есть S и высота пирамиды есть h,
тогда формула ее объема есть:

$V = \frac{1}{3} \cdot S \cdot h$

Правильный тетраэдр

$V = \frac{\sqrt{2}\cdot a^3}{12}$

Площадь поверхности:

$S = \sqrt{3}\cdot a^2$

Прямой круговой конус

Конус это фигура с основанием в виде окружности и имеющая одну вершину, как у пирамиды.
Если площадь основы есть S и длиныа стороны конуса равна h,
то формула объема есть:

$V = \frac{1}{3} \cdot S \cdot h = \frac{1}{3} \cdot \pi \cdot r^2\cdot h$

Формула площади боковой поверхности конуса:

$S=\pi\cdot r \cdot l$

Формула площади полной поверхности конуса (то есть сумма площадей боковой поверхности и основания):

$S=\pi\cdot r(r + l)$

Сфера

Сфера есть шар.
Она имеет радиус — расстояние от центральной точки сферы к поверхности. Если длина радиуса есть R,
то формула объема есть:

$V = \frac{4}{3} \cdot \pi \cdot r^3$

Площадь поверхности:

$S = 4\cdot\pi\cdot r^2$

Цилиндр

Цилиндр это фигура с двумя параллельными окружностями.
Если ралиус основы равен r и высота (расстояние между основами) цилиндра есть h,
то его объем вычисляется по формуле:

$V = \pi \cdot r^2 \cdot h$

Прямой круговой цилиндр

Объём

$V = \pi \cdot r^2 \cdot h$

Площадь боковой поверхности:

$S = 2\cdot\pi\cdot r \cdot h$

Площадь полной поверхности:

$S = 2\cdot\pi\cdot r(h + r)$

Тест: объём и площадь поверхности

Площади и объемы

Площади

История нахождения площадей фигур начинается еще с древнего Вавилона. Уже тогда вычисляли площади прямоугольника, а древние египтяне пользовались методами вычисления площадей различных фигур, похожими на наши методы.

В своих книгах «Начала» известный древнегреческий математик Евклид описывал достаточно большое число способов вычисления площадей многих геометрических фигур. Первые рукописи на Руси, в которых содержатся геометрические сведения, были написаны в $XVI$ веке. В них описаны правила нахождения площадей фигур различных форм.

Сегодня с помощью современных методов можно найти площадь любой фигуры с большой точностью.

Рассмотрим одну из простейших фигур — прямоугольник — и формулу нахождения его площади.

Формула площади прямоугольника

Рассмотрим фигуру (рис. 1), которая состоит из $8$ квадратов со сторонами по $1$ см. Площадь одного квадрата со стороной $1$ см называют сантиметром квадратным и записывают $1\ см^2$.

Площадь данной фигуры (рис. 1) будет равна $8\ см^2$.

Площадь фигуры, которую можно разбить на несколько квадратов со стороной $1\ см$ (например, $p$), будет равна $p\ см^2$.

Готовые работы на аналогичную тему

Другими словами, площадь фигуры будет равна стольким $см^2$, на сколько квадратов со стороной $1\ см$ можно разбить эту фигуру.

Рассмотрим прямоугольник (рис. 2), который состоит из $3$ полос, каждая из которых разбита на $5$ квадратов со стороной $1\ см$. весь прямоугольник состоит из $5\cdot 3=15$ таких квадратов, и его площадь равна $15\ см^2$.

Рисунок 1.

Рисунок 2.

Площадь фигур принято обозначать буквой $S$.

Для нахождения площади прямоугольника нужно его длину умножить на ширину.

Если обозначить буквой $a$ его длину, а буквой $b$ — ширину, то формула площади прямоугольника будет иметь вид:

Определение 1

Фигуры называют равными, если при наложении их одна на другую фигуры совпадут. Равные фигуры имеют равные площади и равные периметры.

Площадь фигуры можно найти как сумму площадей ее частей.

Пример 1

Например, на рисунке $3$ прямоугольник $ABCD$ разбит на две части линией $KLMN$. Площадь одной части равна $12\ см^2$, а другой — $9\ см^2$. Тогда площадь прямоугольника $ABCD$ будет равна $12\ см^2+9\ см^2=21\ см^2$. Найдем площадь прямоугольника по формуле:

\[S=a\cdot b=3\cdot 7=21\ см^2.\]

Как видим, площади, найденные обоими способами, равны.

Рисунок 3.

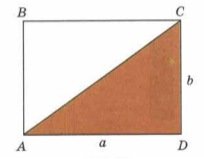
Рисунок 4.

Отрезок $AC$ делит прямоугольник на два равных треугольника: $ABC$ и $ADC$. Значит площадь каждого из треугольников равна половине площади всего прямоугольника.

Определение 2

Прямоугольник с равными сторонами называется квадратом.

Если обозначить сторону квадрата буквой $a$, то площадь квадрата будет находится по формуле:

\[S=a\cdot a=a^2.\]

Отсюда и название квадрат числа $a$.

Пример 2

Например, если сторона квадрата равна $5$ см, то его площадь:

\[S=a^2=5^2\ см^2=25\ см^2.\]

Объемы

С развитием торговли и строительства еще во времена древних цивилизаций появилась необходимость в нахождении объемов. В математике существует раздел геометрии, который занимается изучением пространственных фигур, называемый стереометрией. Упоминания об этом отдельном направлении математики встречались уже в $IV$ веке до н.э.

Древними математиками был выведен способ вычисления объема несложных фигур — куба и параллелепипеда. Все сооружения тех времен были именно такой формы. Но в дальнейшем были найдены способы вычисления объема фигур более сложных форм.

Объем прямоугольного параллелепипеда

Если наполнить формочку влажным песком и потом перевернуть, то получим объемную фигуру, которая характеризуется объемом. Если сделать таких фигур несколько с помощью одной и той же формочки, то получатся фигуры, которые имеют одинаковый объем. Если наполнить формочку водой, то объем воды и объем фигуры из песка также будут равными.

Рисунок 5.

Сравнить объемы двух сосудов можно, наполнив один водой и перелив ее во второй сосуд. Если второй сосуд окажется полностью заполненным, то сосуды имеют равные объемы. Если при этом в первой вода останется, то объем первого сосуда больше объема второго. Если при переливании воды из первого сосуда не удается полностью заполнить второй сосуд, значит объем первого сосуда меньше объема второго.

Объем измеряется с помощью следующих единиц:

$мм^3$ — миллиметр кубический,

$см^3$ — сантиметр кубический,

$дм^3$ — дециметр кубический,

$м^3$ — метр кубический,

$км^3$ — километр кубический.

Пример 3

Например, сантиметр кубический — это объем куба с ребром $1\ см$ (рис.~6).

Замечание 1

Дециметр кубический еще называют литром.

\[1\ л=1\ дм^3.\]

На рисунке $7$ фигура состоит из $4$ кубиков с ребром $1\ см$. объем такой фигуры равен $4\ см^3$.

Рисунок 6.

Рисунок 7.

Рассмотрим прямоугольный параллелепипед длиной $4$ см, шириной $3$ см и высотой $2$ см (рис. 8, а). Разделим его на $2$ слоя толщиной $1$ см (рис. 8, б).

Разделим каждый из слоев на $3$ столбика длиной $4$ см (рис. 8, в), а каждый столбик — на $4$ кубика с ребром $1$ см (рис. 8, г).

Рисунок 8.

Объем каждого кубика равен $1\ см^3$, объем каждого столбика — $4\cdot 1\ см^3=4\ см^3$, объем каждого слоя — $3\cdot 4\ см^3$. Тогда объем всего прямоугольного параллелепипеда — $2\cdot \left(4\cdot 3\right)\ см^3=24\ см^3$.

Таким образом, для вычисления объема прямоугольного параллелепипеда нужно его длину умножить на ширину и на высоту.

Объем фигуры принято обозначать буквой $V$.

Формула объема прямоугольного параллелепипеда:

Определение 3

Куб — прямоугольный параллелепипед с равными ребрами.

Если ребро куба равно $a$, то формула объема куба будет иметь вид:

\[V=a\cdot a\cdot a=a^3.\]

Отсюда и название куб числа $a$.

Формулы объема и площади поверхности. Призма, пирамида

Изучение стереометрии начинается со знания формул. Для решения задач ЕГЭ по стереометрии нужны всего две вещи:

1. Формулы объёма — например, объём куба, объём призмы, объем пирамиды — и формулы площади поверхности.
2. Элементарная логика.

Все формулы объёма и формулы площади поверхности многогранников есть в нашей таблице.

Ты нашел то, что искал? Поделись с друзьями!

Проще всего найти объём куба — это куб его стороны. Вот, оказывается, откуда берётся выражение «возвести в куб».

Объём параллелепипеда тоже легко найти. Надо просто перемножить длину, ширину и высоту.

Объём призмы — это произведение площади её основания на высоту. Если в основании треугольник — находите площадь треугольника. Если квадрат — ищите площадь квадрата. Напомним, что высота — это перпендикуляр к основаниям призмы.

Объём пирамиды — это треть произведения площади основания на высоту. Высота пирамиды — это перпендикуляр, проведенный из её вершины к основанию.

Некоторые задачи по стереометрии решаются вообще без формул! Например, эта.

Объём куба равен . Найдите объём четырёхугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.

Обойдёмся без формул! Просто посчитайте, сколько нужно таких четырёхугольных пирамидок, чтобы сложить из них этот куб 🙂

Очевидно, их 6, поскольку у куба 6 граней.

Иногда в задаче  надо посчитать площадь поверхности куба или призмы.

Напомним, что площадь поверхности многогранника — это сумма площадей всех его граней.

В некоторых задачах каждое ребро многогранника увеличили, например, в три раза. Очевидно, что при этом площадь поверхности увеличится в девять раз, а объём — в раз.

Стереометрия — это просто! Для начала выучите формулы объёма и площади поверхности многогранников и тел вращения. А дальше — читайте о приемах решения задач по стереометрии.

---

Формулы объема, площади поверхности, объем конуса, объем цилиндра, объем шара

Тела вращения, изучаемые в школе, — это цилиндр, конус и шар.

Если в задаче на ЕГЭ по математике вам надо посчитать объем конуса или площадь сферы — считайте, что повезло.

Применяйте формулы объема и площади поверхности цилиндра, конуса и шара. Все они есть в нашей таблице. Учите наизусть. Отсюда начинается знание стереометрии.

Ты нашел то, что искал? Поделись с друзьями!

Смотрите также: Формулы объема и площади поверхности многогранников.
Кроме формул, в решении задач по стереометрии нужны также элементарная логика и пространственное воображение. Есть и свои небольшие секреты.

Например, такой важный факт:

Если все линейные размеры объемного тела увеличить в 2 раза, то площадь его поверхности увеличится в 4 раза, а объем — в 8 раз. 

(ведь , ).

Вот такая задача. Как и остальные на нашем сайте, она взята из банка заданий ФИПИ.

1. Объем конуса равен . Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.

Очевидно, что объем меньшего конуса в раз меньше объема большого и равен двум.

Для решения некоторых задач полезны начальные знания стереометрии. Например — что такое правильная пирамида или прямая призма. Полезно помнить, что у цилиндра, конуса и шара есть еще общее название — тела вращения. Что сферой называется поверхность шара. А, например, фраза «образующая конуса наклонена к плоскости основания под углом 30 градусов предполагает, что вы знаете, что такое угол между прямой и плоскостью. Вам также может пригодиться теорема Пифагора и простые формулы площадей фигур.

Иногда неплохо нарисовать вид сверху. Или, как в этой задаче, — снизу.

2. Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду?

Всё просто — рисуем вид снизу. Видим, что радиус большего круга в раз больше, чем радиус меньшего. Высоты у обоих конусов одинаковы. Следовательно, объем большего конуса будет в раза больше.

Говорят, что хороший чертеж — это уже половина решения. Читайте о том, как строить чертежи в задачах по стереометрии.

Еще один важный момент. Помним, что в задачах части В вариантов ЕГЭ по математике ответ записывается в виде целого числа или конечной десятичной дроби. Поэтому никаких или у вас в ответе в части В быть не должно. Подставлять приближенное значение числа тоже не нужно! Оно обязательно должно сократиться!. Именно для этого в некоторых задачах задание формулируется, например, так: «Найдите площадь боковой поверхности цилиндра, деленную на ».

А где же еще применяются формулы объема и площади поверхности тел вращения? Конечно же, в задаче 14 Профильного ЕГЭ по математике.
Мы тоже расскажем о ней.

---

Отношение объема к площади поверхности любого физического тела. Один из важнейших инженерных приемов.

Отношение объема к площади поверхности любого физического тела. Один из важнейших инженерных приемов.

Представьте себе куб с длиной ребра 1 метр (1 сантиметр, 1 фут, 1 дюйм или 1 «чего Вам угодно»), далее будет метр — для простоты. Объем этого куба равен 1 м³. Каждая сторона имеет площадь1 м² , а вся площадь поверхности этого кубика равна 6 м² — сторон-то шесть. Отношение объема к площади поверхности равно 1:6 = 1/6 (сейчас и далее — без учета размерности).

 

Тепрь представьте себе куб со стороной 3 м.Объем этого куба равен 27 м³ (3х3х3). Каждая сторона имеет площадь 9 м² , а вся площадь поверхности этого кубика равна 54 м². Отношение объема к площади поверхности равно 27:54 = 1/2 = 3/6.

То есть, при росте линейного размера в 3 раза площадь поверхности выросла в 9 раз, но объем вырос в 27 раз. Отношение объема к площади поверхности выросло в 3 раза.

В таблице ниже приведены расчеты для кубов при пошаговом удвоении линейного размера:

Таблица. Сравнение динамик площади поверхности и объема физического тела с ростом линейного размера.

Линейный размер (м)	Площадь поврхности (м2)	Объем (м3)	Отношение объема к площади поверхности
1	6,00	1,00	0,17
2	24,00	8,00	0,33
4	96,00	64,00	0,67
8	384,00	512,00	1,33
16	1 536,00	4 096,00	2,67
32	6 144,00	32 768,00	5,33
64	24 576,00	262 144,00	10,67
128	98 304,00	2 097 152,00	21,33
256	393 216,00	16 777 216,00	42,67
512	1 572 864,00	134 217 728,00	85,33

При росте линейного размера объем возрастает намного быстрее, чем площадь поверхности тела, посколюку объем пропорционален кубу линейного размера, а площадь — квадрату. Этот факт применим не только к телам кубической формы, но и к любым другим телам, естественно при сохранении формы ( или пропорций, если Вам так больше нравится).

Рисунок. Сравнение динамик площади поверхности и объема физического тела с ростом линейного размера.

 

Некоторые житейские примеры важности рассматриваемого факта.

1) Теплоотдача пропорциональна площади поверхности. Теплоемкость — объему тела. Из этого факта напрямую следует, что более крупное здание (той же формы) будет дольше отдавать накопленное за световой день тепло (или нагреваться днем) и потребует меньше энергии на единицу полезной площади — ! полезная площадь прямо пропорциональна внутреннему объему ! — на отопление (кондиционирование).

2) Масса (вес) пропорциональна объему опоры. Нагрузка на грунт — площади поверхности. Из этого факта напрямую следует, что для опоры любой формы существует размер, начиная с которого (при сохранении формы) она уйдет в любой грунт.

3) Ребенок имеет совершенно другое соотношение площадь/объем, чем взрослый человек. Поэтому риски переохлаждения или получения теплового удара для ребенка несоизмеримо выше (что, конечно, отчасти компенсируется другой скоростью обменных процессов у детей).

Формулы площадей всех основных фигур

1. Формула площади равнобедренной трапеции через стороны и угол

b — верхнее основание

a — нижнее основание

c — равные боковые стороны

α — угол при нижнем основании

 

Формула площади равнобедренной трапеции через стороны, (S):

 

Формула площади равнобедренной трапеции через стороны и угол, (S):

 

 

2. Формула площади равнобокой трапеции через радиус вписанной окружности

R — радиус вписанной окружности

D — диаметр вписанной окружности

O — центр вписанной окружности

H — высота трапеции

α, β — углы трапеции

 

Формула площади равнобокой трапеции через радиус вписанной окружности, (S):

СПРАВЕДЛИВО, для вписанной окружности в равнобокую трапецию:

 

 

3. Формула площади равнобедренной трапеции через диагонали и угол между ними

d — диагональ трапеции

α, β — углы между диагоналями

 

Формула площади равнобедренной трапеции через диагонали и угол между ними, (S):

 

 

4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании

m — средняя линия трапеции

c — боковая сторона

α, β — углы при основании

 

Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, (S ):

 

 

5. Формула площади равнобедренной трапеции через основания и высоту

b — верхнее основание

a — нижнее основание

h — высота трапеции

 

Формула площади равнобедренной трапеции через основания и высоту, (S):

 

Площадь поверхности и объем геометрических тел. Прямые призмы. Правильные пирамиды. Круговые цилиндры. Круговые конусы. Шар и его части. Примерно 8 класс (14 лет)

Прямые призмы (Sполн=2Sосн+Sбок; V=Sосн•H)
Куб	Прямоугольный параллелепипед
Правильная треугольная призма	Правильная шестиугольная призма
Правильные пирамиды (Sполн=Sосн+Sбок; V=1/3•Sосн•H)
Тертраэдр	Правильная треугольная пирамида
Правильная четырехугольная пирамида	Правильная шестиугольная пирамида
Sбок— площадь боковой поверхности многогранника, Sполн — площадь полной поверхности многогранника, Sосн — площадь основания многогранника, V — объем многогранника.

Исчисление I — формулы площади и объема

Пол Заметки Онлайн

Ноты

Быстрая навигация

Скачать

• Перейти к
• Ноты

• Проблемы практики

• Проблемы с назначением

• Показать / Скрыть
• Показать все решения / шаги / и т. Д.
• Скрыть все решения / шаги / и т. Д.

• Разделы
• Доказательство различных интегральных свойств
• типов бесконечности
• глав
• приложений интегралов
• Классы

• Алгебра

• Исчисление I

• Исчисление II

• Исчисление III

• Дифференциальные уравнения

• Дополнительно

• Обзор алгебры и триггеров

• Распространенные математические ошибки

• Комплексное число праймер

• Как изучать математику

• Шпаргалки и таблицы

• Разное
• Свяжитесь со мной
• Справка и настройка MathJax
• Мои ученики

• Примечания Загрузки
• Полная книга
• Текущий Глава
• Текущий раздел
• Практика Проблемы Загрузки
• Complete Book — Проблемы только
• Complete Book — Решения
• Проблемы с назначением Загрузки
• Полная книга
• Другие предметы
• Получить URL для загрузки элементов

• Распечатать страницу в текущей форме (по умолчанию)
• Показать все решения / шаги и распечатать страницу
• Скрыть все решения / шаги и распечатать страницу

• Дом
• Классы
• алгебра
  • Предварительные
    • Целочисленные экспоненты
    • Рациональные экспоненты
    • Радикалы
    • полиномов
    • Факторинг Полиномы
    • Rational Expressions
    • Комплексные числа
  • Решение уравнений и неравенств
    • Решения и комплекты решений
    • линейных уравнений
    • приложений линейных уравнений
    • уравнений с более чем одной переменной
    • Квадратичные уравнения — Часть I
    • Квадратичные уравнения — Часть II
    • Квадратичные уравнения: краткое изложение
    • Приложения квадратичных уравнений

    Уравнения

    • , приводимые к квадратичной форме
    • Уравнения с радикалами
    • линейных неравенств
    • Полиномиальное неравенство
    • Рациональное неравенство
    • Уравнения абсолютной стоимости
    • Абсолютное неравенство в значениях
  • Графика и функции
    • График
    • Линии
    • Круги
    • Определение функции
    • Графические функции
    • Объединение функций
    • Обратные функции
  • общих графиков
    • Линии, окружности и кусочные функции
    • Параболы
    • Эллипсы
    • Гипербол
    • Разные функции
    • Преобразования
    • Симметрия
    • Рациональные функции
  • полиномиальных функций
    • делительных полиномов
    • Нули / корни полиномов
    • графических полиномов
    • В поисках нулей полиномов

.

Разница между площадью и объемом (со сравнительной таблицей)

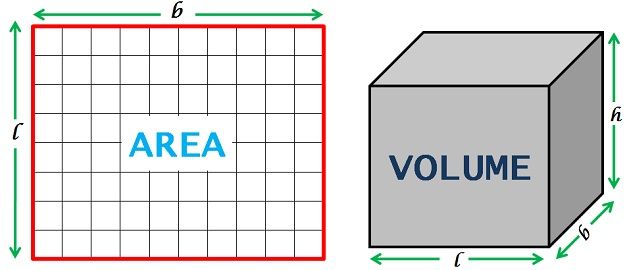Как видите, вокруг нас много объектов, которые имеют определенную площадь или объем, хотя мы их не распознаем. В то время как область является областью, охватываемой фигурой замкнутой плоскости, объем является объемом пространства, занимаемого объектом. Измерение площади производится в квадратных метрах, а измерение объема — в кубических метрах.

Термины площадь и объем являются двумя важными понятиями менструаций, которые широко используются не только в математике, но и в нашей повседневной жизни.В статье делается попытка пролить свет на значительные различия между площадью и объемом. Взгляни на это.

Содержимое: Площадь против Объема

1. Сравнительная таблица
2. Определение
3. Ключевые отличия
4. Заключение

Сравнительная таблица

Основа для сравнения	Площадь	Объем
Значение	Площадь относится к области или пространству плоской фигуры или объекта.	Объем относится к количеству пространства, содержащегося в объекте.
Рисунок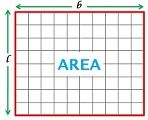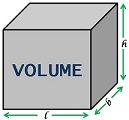
Формы	Плоские фигуры	Твердые тела
Что это?	Количество закрытых помещений	Вместимость твердого тела
Измеряется в	Квадратная единица	Кубическая единица
Сделка с	2 Габаритные формы	3 Габаритные формы

Определение площади

В геометрии площадь объекта есть не что иное, как его размер, т.е.е. это двумерное пространство или область, которую охватывает замкнутая фигура. Он измеряет размер пространства, занимаемого плоским объектом, рассчитывается путем умножения размеров фигуры.

Площадь помогает нам определить, сколько квадратов фиксированного размера потребуется, чтобы покрыть ее. Стандартной единицей площади в соответствии с Международной системой единиц (СИ) является квадратный метр (выраженный в м ² ). Ниже вы можете найти формулу для площади различных объектов:

Формула:

• Площадь площади = сторона × сторона
• Площадь прямоугольника = l × w
• Площадь параллелограмма = b × h
• Площадь треугольника = (б × ч) / 2
• Площадь круга = № ²

, где l — длина
w — ширина
h — высота
b — основание
r — радиус

Определение тома

Объем относится к объему пространства внутри трехмерного объекта, окруженного замкнутой поверхностью, т.е.е. это определяет пространство, которое содержит форма. Кубический метр — это единица СИ объема.

Проще говоря, объем объекта есть не что иное, как его емкость. Например, предположим, что есть полая бутылка, поэтому объем — это количество жидкости, которое она может вместить. Ниже вы можете найти формулу для объема различных объектов:

Формула:

• Объем прямоугольной призмы = l × w × h
• Объем куба = ³
• Объем сферы = (4/3) × π × r ³
• Объем цилиндра = π × r ² × h
• Объем конуса = π × r ² × (ч / 3)

, где, l — длина
Вт — ширина
h — высота
a — край
r — радиус
h — высота

Ключевые различия между областью и объемом

Точка, представленная ниже, важна для разницы между областью и объемом:

1. Область или пространство плоской фигуры или объекта называется областью.Количество пространства, содержащегося в объекте, называется объемом.
2. Плоские фигуры имеют площадь, а сплошные фигуры — объем.
3. Площадь описывает количество закрытого пространства, тогда как объем определяет емкость твердых частиц.
4. Измерение площади производится в квадратных единицах, которые могут быть сантиметрами, ярдами и так далее. Напротив, объем измеряется в кубических единицах.
5. Формы, имеющие два измерения, то есть длину и ширину, имеют площадь. В отличие от этого, формы с тремя измерениями, т.е.е. длина, ширина и высота, есть объем.

Заключение

Поэтому, с учетом вышеизложенного, вы, возможно, ясно поняли, что эти два математических понятия сильно различаются по их использованию и измерению. В то время как область используется для определения пространства, охватываемого плоским объектом, объем используется для определения пространства внутри объекта.

,

Формула площади и объема для геометрических фигур

пи (π) = 3,1415926535 …

Формула периметра
Площадь	4 × сторона
Прямоугольник	2 × (длина + ширина)
Параллелограмм	2 × (сторона1 + сторона2)
Треугольник	side1 + side2 + side3
Обычный n-многоугольник	n × сторона
Трапеция	высота × (base1 + base2) / 2
Трапеция	base1 + base2 + высота × [csc (theta1) + csc (theta2)]
Круг	2 × пи × радиус
Эллипс	4 × радиус1 × E (к, пи / 2) E (k, pi / 2) — полный эллиптический интеграл второго рода k = (1 / radius1) × sqrt (radius1 2 — radius2 2 )
Формула площади
Площадь	сторона 2
Прямоугольник	длина × ширина
Параллелограмм	основание × высота
Треугольник	основание × высота / 2
Обычный n-многоугольник	(1/4) × n × сторона 2 × детская кроватка (pi / n)
Трапеция	высота × (base1 + base2) / 2
Круг	пи × радиус 2
Эллипс	пи × радиус1 × радиус2
Куб (поверхность)	6 × сторона 2
Сфера (поверхность)	4 × пи × радиус 2
Цилиндр (поверхность сбоку)	периметр круга × высота
	2 × пи × радиус × высота
Цилиндр (вся поверхность)	Области верхних и нижних кругов + Площадь стороны
	2 (пи × радиус 2 ) + 2 × пи × радиус × высота
Конус (поверхность)	пи × радиус × сторона
Тора (поверхность)	пи 2 × (радиус2 2 — радиус1 2 )
Объемная формула
Cube	сторона 3
Прямоугольная призма	side1 × side2 × side3
Сфера	(4/3) × пи × радиус 3
Эллипсоид	(4/3) × пи × радиус1 × радиус2 × радиус3
Цилиндр	пи × радиус 2 × высота
Конус	(1/3) × пи × радиус 2 × высота
Пирамида	(1/3) × (базовая площадь) × высота
Тора	(1/4) × пи 2 × (r1 + r2) × (r1 — r2) 2

Источник: Spiegel, Мюррей Р.Математическое пособие по формулам и таблицам.
Очерк серии Шаума по математике. McGraw-Hill Book Co., 1968.

,

Исчисление III — Площадь и объем пересмотрено

Пол Заметки Онлайн

Ноты

Быстрая навигация

Скачать

• Перейти к
• Ноты

• Проблемы практики

• Проблемы с назначением

• Показать / Скрыть
• Показать все решения / шаги / и т. Д.
• Скрыть все решения / шаги / и т. Д.

• Разделы
• Площадь поверхности
• Линейные интегралы Введение
• глав
• приложений частных производных
• Линейные интегралы
• Классы

• Алгебра

• Исчисление I

• Исчисление II

• Исчисление III

• Дифференциальные уравнения

• Дополнительно

• Обзор алгебры и триггеров

• Распространенные математические ошибки

• Комплексное число праймер

• Как изучать математику

• Шпаргалки и таблицы

• Разное
• Свяжитесь со мной
• Справка и настройка MathJax
• Мои ученики

• Примечания Загрузки
• Полная книга
• Текущий Глава
• Текущий раздел
• Практика Проблемы Загрузки
• Complete Book — Проблемы только
• Complete Book — Решения
• Текущая глава — только проблемы
• Текущая глава — Решения
• Проблемы с назначением Загрузки
• Полная книга
• Текущий Глава
• Другие предметы
• Получить URL для загрузки элементов

• Распечатать страницу в текущей форме (по умолчанию)
• Показать все решения / шаги и распечатать страницу
• Скрыть все решения / шаги и распечатать страницу

• Дом
• Классы
• алгебра
  • Предварительные
    • Целочисленные экспоненты
    • Рациональные экспоненты
    • Радикалы
    • полиномов
    • Факторинг Полиномы
    • Rational Expressions
    • Комплексные числа
  • Решение уравнений и неравенств
    • Решения и комплекты решений
    • линейных уравнений
    • приложений линейных уравнений
    • уравнений с более чем одной переменной
    • Квадратичные уравнения — Часть I
    • Квадратичные уравнения — Часть II
    • Квадратичные уравнения: краткое изложение
    • Приложения квадратичных уравнений

    Уравнения

    • , приводимые к квадратичной форме
    • Уравнения с радикалами
    • линейных неравенств
    • Полиномиальное неравенство
    • Рациональное неравенство
    • Уравнения абсолютной стоимости
    • Абсолютное неравенство в значениях
  • Графика и функции
    • График
    • Линии
    • Круги
    • Определение функции
    • Графические функции
    • Объединение функций
    • Обратные функции
  • общих графиков
    • Линии, Круги a

.