Размерность коэффициента теплоотдачи: Коэффициент теплоотдачи, формула и примеры
Коэффициент теплоотдачи, формула и примеры
Определение и формула коэффициента теплоотдачи
Конвективный теплообмен — обмен теплотой между частями жидкости (газа), имеющими разную температуру или между жидкостью (газом) и твердым телом. Конвективный теплообмен между жидкостью и твердым телом называют теплоотдачей.
Этот коэффициент часто используют в гидроаэродинамике, когда исследуют конвективный теплообмен. Часто ее обозначают буквой . Коэффициент равен:
где — плотность теплового потока, — температурный напор. Величина q — это количество теплоты, которое передается через единичную площадь поверхности тела в единицу времени. находят как модуль разности температур жидкости и поверхности тела. Иногда температурный напор находят, например, в случае обтекания тела потоком сжимаемой жидкостью, считают равным модулю разности температуры жидкости далеко от тела и температурой поверхности тела, которая была бы в отсутствии теплообмена.
Коэффициент теплоотдачи зависит от скорости потока носителя тепла, вида течения, какова геометрия поверхности твердого тела и т.д. Это сложная величина и ее невозможно определить общей формулой. Обычно коэффициент теплоотдачи находят экспериментально.
Так, для условий свободной конвекции воздуха: (Вт/м2К), воды: (Вт/м2К). При вынужденной конвекции величины коэффициента теплоотдачи колеблются в пределах: для воздуха: (Вт/м2К), для воды: (Вт/м2К).
Формула Ньютона-Рихмана
Коэффициент теплоотдачи входит в выражение для потока тепла в веществе жидкой или газообразной среды с интенсивным изменением температуры при увеличении расстояния от охлаждаемого или нагреваемого объекта:
где — количество теплоты, которая отводится от поверхности, имеющую площадь S, — температура вещества (жидкости, газа), — температура поверхности тела. Выражение (2) называется формулой Ньютона — Рихмана.
Так как интенсивность теплообмена может изменяться при передвижении вдоль площади соприкосновения жидкого носителя с поверхностью твердого тела, вводят местный коэффициент теплоотдачи, который равен:
На практике чаще применяют средний коэффициент теплоотдачи , вычисляя его по формуле:
где температуры берут средние для поверхности и для вещества.
Дифференциальное уравнение теплоотдачи
Дифференциальное уравнение теплоотдачи показывает связь между коэффициентом теплоотдачи и полем температур среды (жидкости или газа):
где , — градиент температуры, индекс n=0 значит то, что градиент берут на стенке.
Критерий Нуссельта
Критерий Нуссельта () является характеристикой теплообмена на границе между жидкостью и стеной:
где — характерный линейный размер, — коэффициент теплопроводности жидкости. Для стационарного процесса критерий Нуссельта находят, используя критериальное уравнение конвективного теплообмена:
где постоянные. — критерий Рейнольдса, — критерий Прандтля, — критерий Грасгофа.
Коэффициент теплоотдачи и его связь с коэффициентом теплопередачи
Коэффициентом теплопередачи через плоскую стенку связан с коэффициентами теплоотдачи выражением:
где — коэффициент теплоотдачи от первой среды к стенке, — коэффициент теплоотдачи от стенки ко второй среде, — толщина стенки, — коэффициент теплопроводности стенки.
Единицы измерения
Основной единицей измерения коэффициента теплоотдачи в системе СИ является:
=Вт/м2К
Примеры решения задач
Расчет коэффициента теплоотдачи на плоских и гофрированных поверхностях
Во многих инженерных задачах, связанных с теплопередачей, например, при проектировании теплообменных аппаратов и радиаторов охлаждения, важное значение имеет расчет коэффициента теплоотдачи. Коэффициент теплоотдачи, который чаще всего рассчитывается с помощью эмпирических формул, характеризует интенсивность теплообмена на поверхности твердого тела. В этой статье мы расскажем и покажем, как рассчитать коэффициент теплоотдачи на плоской поверхности с помощью среды численного моделирования COMSOL Multiphysics®.
Что такое коэффициент теплоотдачи?
Рассмотрим нагретую стенку или поверхность, находящуюся в контакте с потоком жидкости. Перенос теплоты в жидкости определяется преимущественно конвекцией. Аналогично, конвекцией определяется перенос теплоты через твердую стенку, омываемую с двух сторон двумя разными жидкостями, например, в теплообменных аппаратах. Интенсивность теплопередачи в обоих случаях пропорциональна разности температур, а коэффициент пропорциональности, собственно, и является коэффициентом теплоотдачи. Коэффициент теплоотдачи характеризует теплообмен между поверхностью твердого тела и жидкостью.
В математическом смысле h— это отношение плотности теплового потока на стенке к разности температур стенки и жидкости; таким образом,
(1)
h=\dfrac
{q\prime \prime}
{(T_w {-} T_
{\infty}
)}
где q^{\prime \prime}— плотность теплового потока, T_w— температура стенки, а T_\infty— характерная температура жидкости.
В качестве характерной температуры жидкости могут выступать температура жидкости вдали от стенки или среднемассовая температура в трубе.
Если объект находится в неограниченно большом объеме воздуха, можно предположить, что температура воздуха вдали от поверхности объекта является постоянной и известной величиной. Такие задачи теплообмена называются внешними.
Рассмотрим пристеночную область (пусть плоскость стенки расположена по нормали к оси y, и y = 0 соответствует поверхности стенки). С учетом сделанного выше допущения очевидно, что при выполнении условия прилипания на стенке (то есть отсутствия проскальзывания) вблизи стенки образуется тонкая пленка почти неподвижной жидкости. Следовательно, перенос теплоты в этой пленке осуществляется исключительно за счет теплопроводности.
Математически этот процесс описывается уравнением [1]:
(2)
q ^{\prime \prime}
=-k\bigg(\dfrac
{\partial T}{\partial y}\bigg)_{y=0}
Здесь k— коэффициент теплопроводности жидкости, а производная от T рассчитывается в области жидкости.
Из уравнений (1) и (2) следует, что коэффициент теплоотдачи можно определить следующим образом:
(3)
h=\dfrac{-k \bigg(\dfrac{\partial T} {\partial y}
\bigg)_{y=0}}{T_w {-} T_\infty}
Расчет коэффициента теплоотдачи в COMSOL Multiphysics®
На практике измерить градиент температуры на стенке довольно затруднительно. Кроме того, хотелось бы эффективно анализировать процессы теплообмена вблизи твердой поверхности без привлечения значительных вычислительных ресурсов. Поэтому для расчета коэффициента теплоотдачи, как правило, используются неаналитические методы.
Широко признанным методом расчета коэффициента теплоотдачи является использование уравнений подобия для безразмерного числа Нуссельта. Эти уравнения позволяют быстро рассчитать коэффициент теплоотдачи для разных условий теплообмена, в том числе при свободной и вынужденной конвекции в задачах внешнего обтекания и при течении в каналах. Однако этот подход можно использовать только для объектов правильной геометрической формы: для горизонтальных и вертикальных плоских поверхностей, цилиндров и сфер.
Если поверхность теплообмена в задаче имеет более сложную форму, коэффициент теплоотдачи можно рассчитать с помощью моделирования сопряженного теплообмена.
Рассмотрим эти два варианта решения задачи:
- Расчет коэффициента теплоотдачи на поверхностях простой геометрической формы (например, на плоской пластине):
- Моделирование сопряженного теплообмена
- Расчетные формулы; область течения не моделируется
- Вычисление коэффициента теплоотдачи на поверхностях сложной геометрической формы (например, на гофрированной пластине)
Отметим, что очень важно принимать во внимание режим течения жидкости, поскольку коэффициент теплоотдачи зависит от механизмов переноса теплоты в жидкости. В обоих случаях рассмотрим наиболее реалистичный вариант быстрого течения, например, в системе вентиляции или устройстве охлаждения электронной микросхемы. Таким образом, модель должна учитывать дополнительные механизмы переноса теплоты, обусловленные турбулентностью.
Пример 1. Теплообмен при вынужденном обтекании плоской горизонтальной пластины
Рассмотрим задачу об обтекании горизонтальной плоской пластины длиной 5 м, на которой задана постоянная плотность теплового потока 10 Вт/м2. Пластина обдувается воздухом со средней скоростью 0,5 м/с и температурой 283 K. На рисунке ниже представлена схема области течения и показаны профили скорости и температуры в пределах динамического (\delta ) и температурного (\delta {T}) пограничных слоев при ламинарном режиме обтекания.
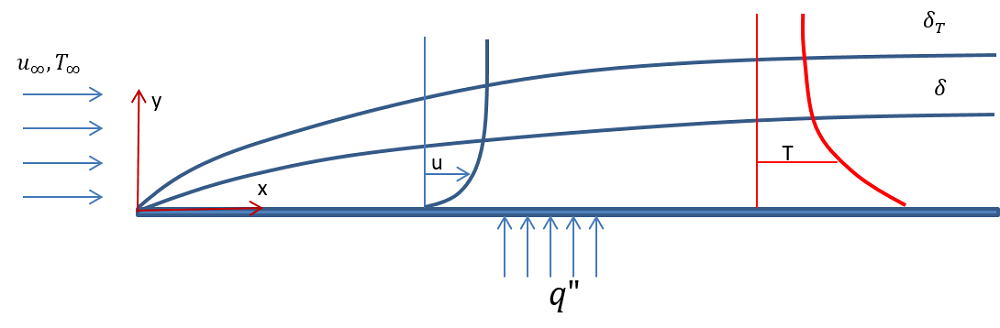
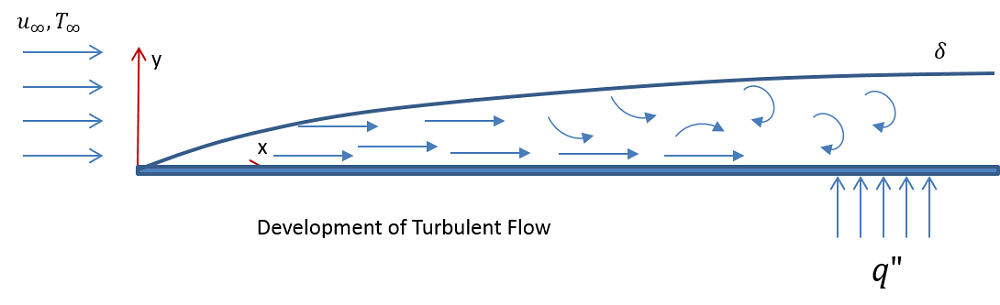
Схематическое изображение ламинарного (сверху) и турбулентного (снизу) пограничных слоев на горизонтальной пластине.
Моделирование сопряженного теплообмена
В COMSOL Multiphysics поставленную задачу можно решить численно, если воспользоваться интерфейсом Conjugate Heat Transfer (Сопряженный теплообмен), который позволяет рассчитать поля течения и температуры в жидкости. Поля скорости и давления рассчитываются в области, занятой воздухом, а поле температуры ещё и в самой пластине.
На следующем рисунке показано распределение температуры в пределах расчетной области, включающей пластину и воздух. В области течения формируются температурный и динамический погранслои, которые занимают область над пластиной толщиной около 2 см.
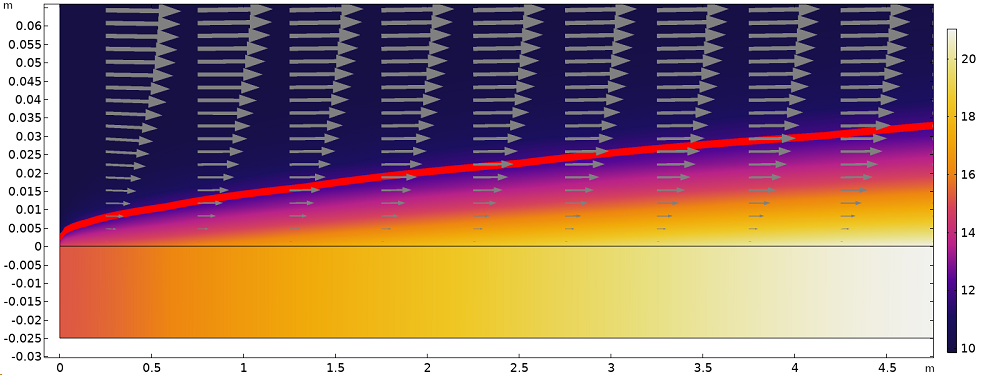
Распределение температуры (график скалярного поля), изотерма на 11 °C (красная линия) и поле скорости (стрелки), показывающие температурный и динамический погранслои у поверхности пластины (масштабы осей не совпадают).
По результатам моделирования можно рассчитать плотность теплового потока, если обратиться к соответствующей встроенной переменной постобработки. Если разделить найденное значение на разность температур (T_w-T_\infty), получим коэффициент теплоотдачи (уравнение 3). На графике ниже показано, как изменяется рассчитанное значение коэффициента теплоотдачи вдоль пластины.
Расчет коэффициента теплоотдачи по формулам для числа Нуссельта
Уравнение для расчета числа Нуссельта при вынужденном обтекании плоской пластины можно найти в литературных источниках (например, в [1]).
Во втором варианте расчета мы решим ту же задачу, но без моделирования области течения; то есть мы воспользуемся формулами для расчета коэффициента теплоотдачи. В этом случае расчетная область включает в себя только твердое тело (пластину). Плотность теплового потока, передаваемая с поверхности нагретой пластины холодной жидкости, задается с помощью граничного условия Heat Flux (Тепловой поток). В настройках этого граничного условия предусмотрен вариант, позволяющий задать коэффициент теплоотдачи на границе с помощью встроенных формул для расчета числа Нуссельта, как показано ниже. Еще раз отметим, что эти формулы уже имеются в COMSOL Multiphysics.
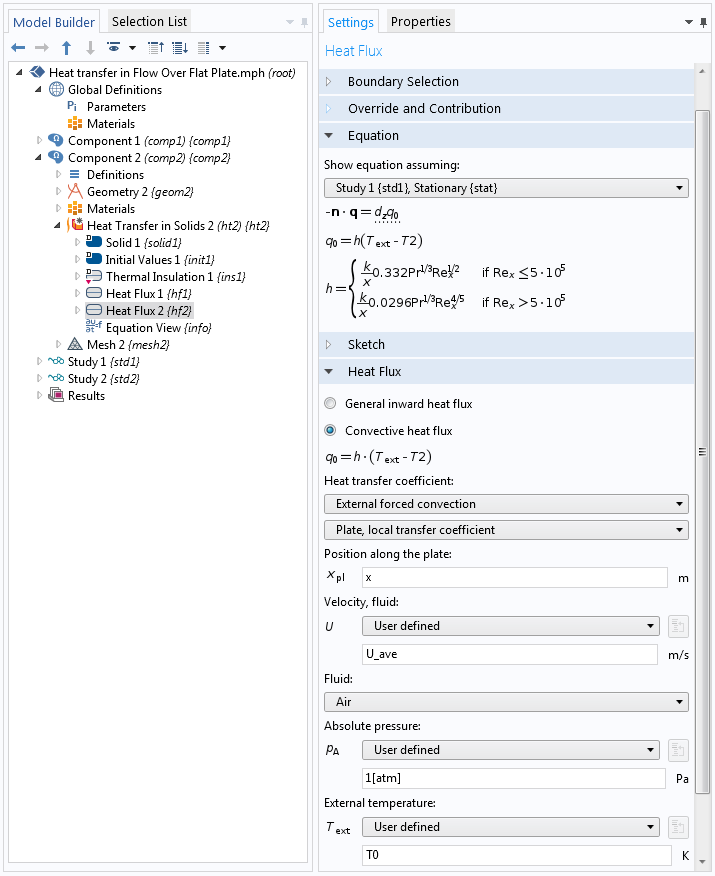
Настройки граничного условия Heat Flux (Тепловой поток).
С помощью этого условия можно рассчитать поле температуры в пластине. Зная коэффициент теплоотдачи на поверхности пластины, заданный в граничном условии Heat Flux (Тепловой поток), можно рассчитать плотность теплового потока: q=h\cdot(T_\infty-T).
Расчет коэффициента теплоотдачи
Рассчитать, как изменяется коэффициент теплоотдачи по длине пластины, можно с помощью любого из двух описанных выше методов. На рисунке ниже показано сравнение результатов расчета коэффициента теплоотдачи двумя методами.
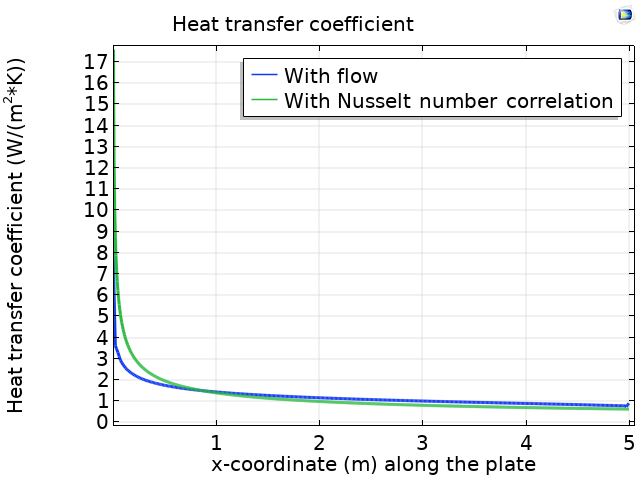
Сравнение значений коэффициента теплоотдачи на плоской пластине, рассчитанных методом моделирования сопряженного теплообмена (синяя линия) и с помощью уравнений для числа Нуссельта (зеленая линия).
Как видно на графике, значения, полученные с помощью уравнений для числа Нуссельта, и значения, рассчитанные на основе численного моделирования сопряженного теплообмена, почти идентичны.
Интерес представляет интенсивность теплообмена на пластине, рассчитанная этими двумя методами:
- Формула для расчета числа Нуссельта: 50 Вт/м
- Сопряженный теплообмен: 49,884 Вт/м
В некоторых задачах эмпирические формулы для числа Нуссельта позволяют рассчитать плотность теплового потока с достаточно высокой точностью. Теперь рассмотрим ситуацию, когда теплообмен происходит на поверхностии сложной формы, для которой нет формул расчета числа Нуссельта, и решить задачу можно только численно.
Пример 2. Течение у гофрированной поверхности горизонтальной пластины
Рассмотрим задачу с теми же исходными условиями, что и в первом случае, но только теперь верхняя поверхность пластины пусть будет гофрированной. На рисунке ниже представлена схема, иллюстрирующая постановку задачи. В этой модели одна из секций верхней поверхности пластины гофрирована. Остальные части пластины плоские.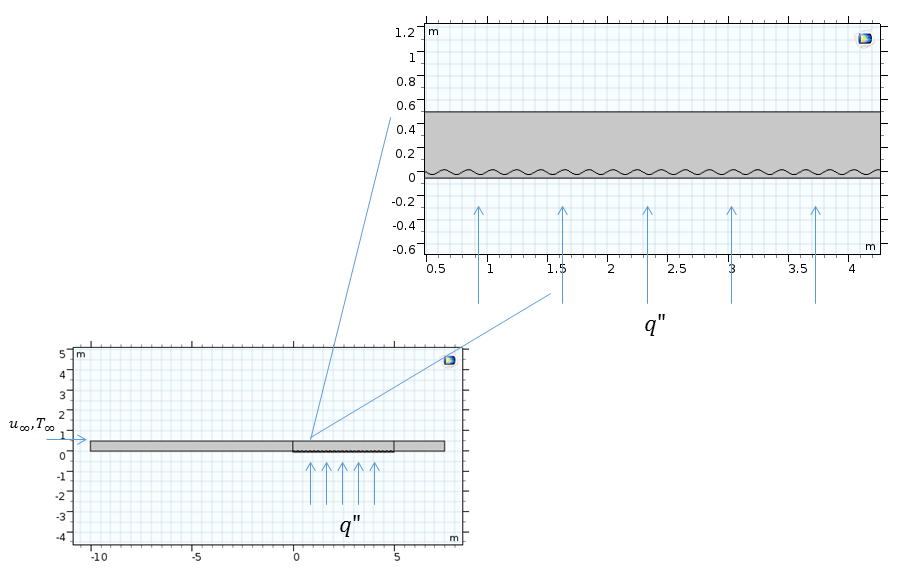
Схема течения на горизонтальной пластине.
При такой форме поверхности стенки в пристеночной области появляются зоны рециркуляции, в результате чего интенсивность теплообмена повышается. На рисунке ниже представлено распределение температуры и линии тока.
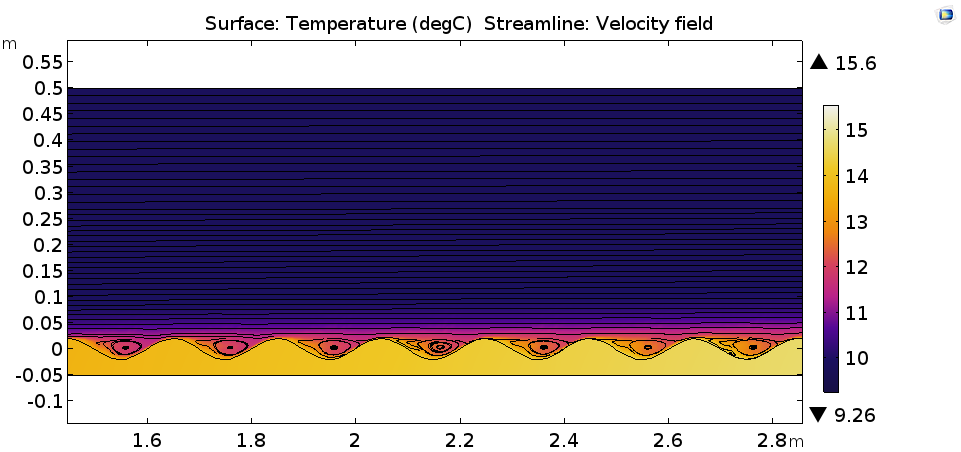
Распределение температуры в градусах Цельсия (поверхность) и поле скорости (линии тока).
На графике слева показано изменение коэффициента теплоотдачи вдоль гофрированной пластины. В задачах со сложной формой поверхности теплообмена, как например при обтекании гофрированной пластины, коэффициент теплоотдачи зависит от нескольких факторов: поля температуры, поля скорости и геометрических параметров поверхности теплообмена (например, высоты гофры). Таким образом, коэффициент теплоотдачи оказывается выше, чем в случае плоской пластины (см. рисунок справа).
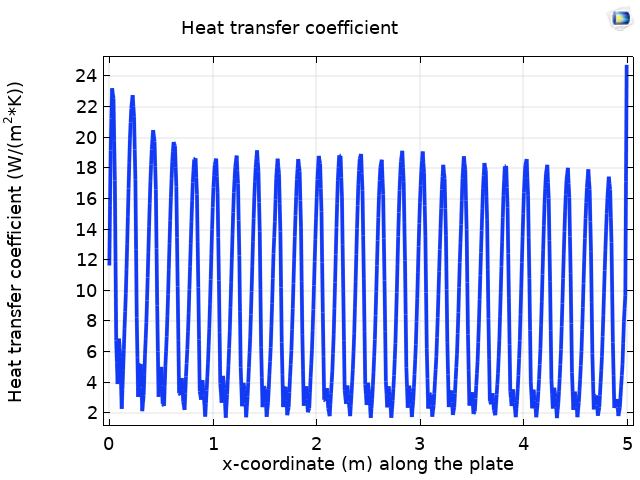
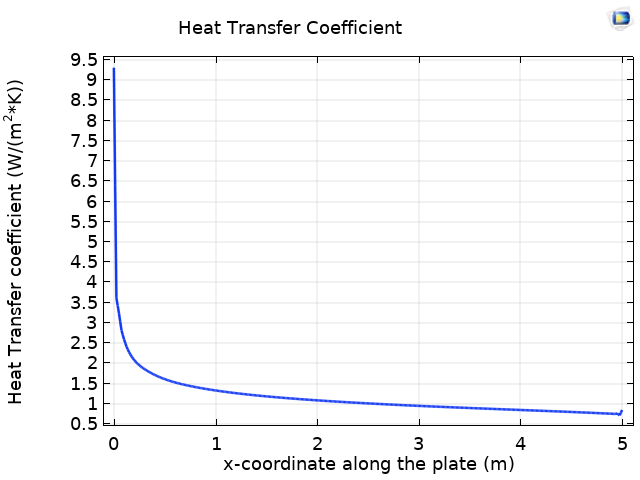
Изменение коэффициента теплоотдачи вдоль гофрированной пластины (слева) и вдоль плоской пластины (справа).
Для моделирования сопряженного теплообмена в моделях со сложной формой поверхностей могут потребоваться значительные вычислительные ресурсы, поэтому иногда предпочтение отдается альтернативным методам решения задачи. Хорошим вариантом решения является замена поверхности сложной формы на простую и подстановка значений коэффициента теплоотдачи, полученных на поверхности сложной формы с учетом геометрических параметров, поля скорости и разности температур. Следует отметить, что, даже если поверхность не является изотермической или если плотность теплового потока не постоянна, значение коэффициента теплоотдачи все равно представляет интерес для некоторых конфигураций, не слишком сильно отличающихся от исходной модели.
Для проверки рассмотрим простой вариант задачи о расчете коэффициента теплоотдачи на омываемой потоком гофрированной поверхности пластины. На основе полученных данных можно определить средний коэффициент теплоотдачи, который затем легко использовать в модели с плоской поверхностью пластины. Корректность такого приближенного подхода можно проверить, если проанализировать полный тепловой поток с поверхности или коэффициент теплоотдачи на основе моделирования сопряженного теплообмена.
Заключение
В этой статье мы рассказали о двух методах расчета коэффициента теплоотдачи. При моделировании сопряженного теплообмена можно использовать встроенные переменные COMSOL Multiphysics, содержащие значения плотности теплового потока. Применение граничного условия Heat Flux (Тепловой поток) и формул для расчета числа Нуссельта позволяет решать задачи о теплообмене на поверхностях простой формы. Также мы кратко обсудили, как использовать упрощенную геометрическую модель для получения данных о коэффициенте теплоотдачи на поверхностях сложной формы.
Дальнейшие шаги
Нажмите на кнопку ниже, чтобы получить дополнительную информацию о специализированных функциях моделирования теплообмена в среде численного моделирования COMSOL®.
Опробуйте рассмотренные методы с помощью учебных моделей:
Список литературы
- A. Bejan et al., Heat Transfer Handbook (Справочник по теплопередаче), John Wiley & Sons, 2003.
Коэффициент теплопередачи, формула и примеры
Определение и формула коэффициента теплопередачи
Процесс теплопередачи можно разделить на теплоотдачу энергии горячим веществом стенке, процесс теплопроводности внутри стенки и теплоотдачу стенки энергии холодному веществу.
Поток тепла при стационарной теплопередаче величина постоянная, то есть не зависит от времени и координат.
Теплопередача через плоскую стенку
Рассмотрим плоскую стенку, через которую происходит теплопередача. Поток тепла через нее равен:
где — температура холодного вещества (), — температура горячего вещества, S — площадь стенки, — коэффициент теплопередачи.
Коэффициентом теплопередачи через плоскую стенку является физическая величина () равная:
где — коэффициент теплоотдачи от первой среды к стенке, — коэффициент теплоотдачи от стенки ко второй среде, — толщина стенки, — коэффициент теплопроводности стенки.
Теплопередача через цилиндрическую стенку
Поток тепла свозь стенку в виде цилиндра вычисляют при помощи формулы:
где — линейный коэффициент теплопередачи, — высота цилиндра.
Линейным коэффициентом теплопередачи через стенку в виде цилиндра является физическая величина () равная:
где — внутренний диаметр цилиндра, — внешний диаметр цилиндра. Для цилиндрических стенок, у которых для расчета теплопередачи применяют формулы (1) и (2) для плоской стенки. Если цилиндр (труба) выполнен из материала с высокой теплопроводностью, то величина термического сопротивления () стенки стремится к нулю ( ), тогда коэффициент теплопроводности рассчитывают по формуле:
Теплопередача через шаровую стенку
Поток тепла через шаровую стенку с внутренним диаметром и наружным — , которая разделяет две среды с постоянными температурами и равен:
Линейным коэффициентом теплопередачи через стенку в виде шара является физическая величина () равная:
Единицы измерения коэффициента теплопередачи
Основной единицей измерения коэффициента теплопередачи в системе СИ является:
=Вт/м2К
=Вт/мК
=Вт/К
Примеры решения задач
Основной закон теплоотдачи. Коэффициент теплоотдачи. — Студопедия
Согласно закону Ньютона (1643 — 1717) и Рихмана (1711 — 1753 гг.) тепловой поток в процессе теплоотдачи пропорционален площади поверхности теплообмена F и разности температур поверхности tc и жидкости t ж:
Q = aF·|tc— t ж|. (5.5)
В процессе теплоотдачи независимо от направления теплового потока Q (от стенки к жидкости или наоборот) значение его принято считать положительным, поэтому разность tc— t ж берут по абсолютной величине.
Коэффициент пропорциональности a называется коэффициентом теплоотдачи; его единица измерения Вт/(м2·К). Он характеризует интенсивность процесса теплоотдачи. Численное значение его равно тепловому потоку от единичной поверхности теплообмена при разности температур поверхности и жидкости в 1 К.
Коэффициент теплоотдачи обычно определяют экспериментально, измеряя тепловой поток Q и разность температур Δt = tc — tж в процессе теплоотдачи от поверхности известной площади F. Затем по формуле (5.5) рассчитывают a. При проведении тепловых расчетов по этой формуле определяют одно из значений Q, F или Δt. При этом a находят по результатам обобщения ранее проведенных экспериментов.
Строго говоря, выражение (5.5) справедливо лишь для дифференциально малого участка поверхности dF, т. е.
dQ = a·dF·|tc— t ж|, (5.6)
поскольку коэффициент теплоотдачи может быть не одинаковым в разных точках поверхности тела. Для расчета полного потока теплоты от всей поверхности нужно проинтегрировать обе части уравнения (5.6) по поверхности
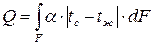 . (5.7)
. (5.7)
Обычно температура поверхности принимается постоянной tc = const, тогда
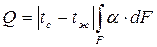 . (5.8)
. (5.8)
В расчетах используются понятия среднего по поверхности коэффициента теплоотдачи:
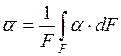 , (5.9)
, (5.9)
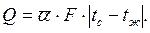 (5.10)
(5.10)
Значение коэффициента теплоотдачи a зависит от физических свойств жидкости и характера ее движения.
Локальный коэффициент теплоотдачи при продольном обтекании тонкой пластины.
Рассмотрим процесс теплоотдачи от потока теплоносителя к продольно омываемой им пластине. Скорость и температура набегающего потока постоянны и равны wж и t ж (рис. 5.2).
Как уже отмечалось, частицы жидкости, непосредственно соприкасающиеся с поверхностью, адсорбируются («прилипают») к ней. Соприкасаясь с неподвижным слоем, тормозятся и более удаленные от поверхности слои жидкости. Зона потока, в которой наблюдается уменьшение скорости (w < wж), вызванное вязким взаимодействием жидкости с поверхностью, называется гидродинамическим пограничным слоем. За пределами пограничного слоя течет невозмущенный поток. Четкой границы между ними нет, так как скорость w по мере удаления от поверхности постепенно (асимптотически) возрастает до wж. За толщину гидродинамического пограничного слоя условно принимают расстояние от поверхности до точки, в которой скорость w отличается от скорости невозмущенного потока wж незначительно (порядка 1%).
На начальном участке (при малых значениях координаты х) гидродинамический слой очень тонок (в лобовой точке с координатой х = 0 толщина равна нулю) и течение в нем ламинарное — струйки жидкости движутся параллельно, не перемешиваясь. При удалении от лобовой точки толщина пограничного слоя растет. На некотором расстоянии х = хкр ламинарное течение становится неустойчивым. В пограничном слое появляются вихри (турбулентные пульсации скорости). Постепенно турбулентный режим течения распространяется почти на всю толщину гидродинамического пограничного слоя. Лишь около самой поверхности пластины сохраняется тонкий ламинарный, или вязкий подслой, где скорость невелика и вязкость гасит турбулентные вихри.
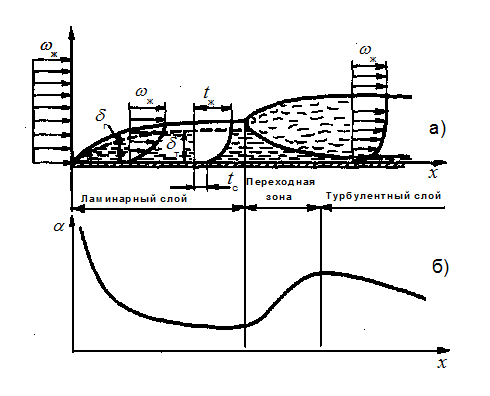
Рис. 5.2. Образование пограничного слоя (а) и распределение местного (локального) коэффициента теплоотдачи (б) при продольном обтекании тонкой пластины.
Аналогичным образом осуществляется и тепловое взаимодействие потока с пластиной. Частицы жидкости, «прилипшие» к поверхности, имеют температуру, равную температуре поверхности tc. Соприкасающиеся с этими частицами движущиеся слои жидкости охлаждаются, отдавая им свою теплоту. От соприкосновения с этими слоями охлаждаются следующие более удаленные от поверхности слои потока — так формируется тепловой пограничный слой, в пределах которого температура меняется от tc на поверхности до tж в невозмущенном потоке. По аналогии с гидродинамическим пограничным слоем толщина теплового пограничного слоя δТ принимается равной расстоянию от поверхности до точки, в которой избыточная температура жидкости q = t — tс отличается от избыточной температуры невозмущенного потока qж = tж — tc на малую величину (обычно на 1 %).
С удалением от лобовой точки количество охлаждающейся у пластины жидкости увеличивается, и толщина теплового пограничного слоя возрастает аналогично возрастанию dг. В общем случае толщины теплового и гидродинамического слоев не равны, но часто достаточно близки друг к другу, особенно в газах.
При ламинарном течении тепловой поток от охлаждающейся в пограничном слое жидкости переносится к поверхности пластины только за счет теплопроводности. При этом плотность теплового потока по толщине пограничного слоя неодинакова: на внешней границе q = 0, ибо дальше жидкость не охлаждается; по мере приближения к поверхности значение q возрастает. Для качественного анализа можно предположить, что плотность теплового потока q по всей толщине пограничного слоя такая же, как и у поверхности. Это условие соответствует задаче о переносе теплоты теплопроводностью через плоскую стенку (пограничный слой толщиной δТ с температурами tc и tж на поверхностях). Согласно решению этой задачи Q ~ l∙F∙ (tc — tж)/δТ. Сравнивая это выражение с формулой (5.5), получим для качественных оценок
a ~ l / dт. (5.11)
В переходном, а тем более, в турбулентном режиме основное термическое сопротивление сосредоточено в тонком ламинарном подслое, поэтому формула (5.11) приближенно пригодна для оценок и в этих режимах, если вместо δТ подставлять значение толщины ламинарного подслоя.
С увеличением толщины теплового пограничного слоя при ламинарном течении жидкости у поверхности пластины интенсивность теплоотдачи уменьшается. В переходной зоне общая толщина пограничного слоя продолжает возрастать, однако значение a при этом увеличивается, потому что толщина ламинарного подслоя убывает, а в образующемся турбулентном слое тепло переносится не только теплопроводностью, но и конвекцией, т. е. более интенсивно. В результате суммарное термическое сопротивление теплоотдачи убывает.
После стабилизации толщины ламинарного подслоя в зоне развитого турбулентного режима коэффициент теплоотдачи вновь начинает убывать из-за возрастания общей толщины пограничного слоя.
Из формулы (9.11) видно, что коэффициент теплоотдачи к газам, обладающим малой теплопроводностью, будет ниже, чем коэффициент теплоотдачи к капельным жидкостям, а тем более к жидким металлам.
Для получения высоких коэффициентов теплоотдачи к газам стараются каким-либо способом уменьшить толщину пограничного слоя. Проще всего для этого увеличить скорость течения газа. Интенсификация теплоотдачи происходит и при резкой искусственной турбулизации пограничного слоя струями, направленными по нормали к поверхности. С помощью системы из множества струй можно обеспечить высокие значения a от достаточно протяженной поверхности. Так, в воздушных струях с относительно невысокими скоростями истечения (w » 60 м/с) удается достигать значений a = 200¸300 Вт/(м2∙К). При обычном продольном обтекании протяженных поверхностей толщина пограничного слоя сравнительно велика, а коэффициент теплоотдачи к воздуху при таких скоростях обычно ниже 100 Вт/(м2∙К).
Локальный коэффициент теплоотдачи при течении теплоносителя внутри трубы.
При течении жидкости в трубе толщина пограничного слоя вначале растет симметрично по всему периметру (рис. 9.3, а), до тех пор, пока слои с противоположных стенок не сольются на оси трубы. Дальше движение стабилизируется и фактически гидродинамический (и тепловой) пограничный слой заполняет все сечение трубы. В зависимости от конкретных условий пограничный слой на начальном участке может успеть (или не успеть) перейти в турбулентный. Соответственно стабилизированный режим течения в трубе будет либо турбулентным с ламинарным подслоем около стенки, либо ламинарным по всему сечению.
В связи с особенностями течения жидкости в трубе изменяется и само понятие коэффициента теплоотдачи. Для пластины коэффициент a рассчитывался как отношение плотности теплового потока q к разности температур внешнего невозмущенного потока и поверхности (или наоборот при tc > tж). В трубе пограничный слой занимает все сечение и невозмущенного потока нет, поэтому под коэффициентом теплоотдачи понимают отношение плотности теплового потока q к разности температуры стенки и среднемассовой температуры жидкости, протекающей через данное сечение трубы.
Локальный коэффициент теплоотдачи от трубы к текущей в ней жидкости изменяется лишь на начальном участке (рис. 9.3, б), а на участке стабилизированного течения aст = const, поскольку толщина пограничного слоя (dт = r) постоянна. С увеличением скорости течения теплоносителя в трубе aст возрастает из-за уменьшения толщины ламинарного подслоя, а с увеличением диаметра трубы уменьшается, поскольку растёт толщина всего пограничного слоя dт = r.
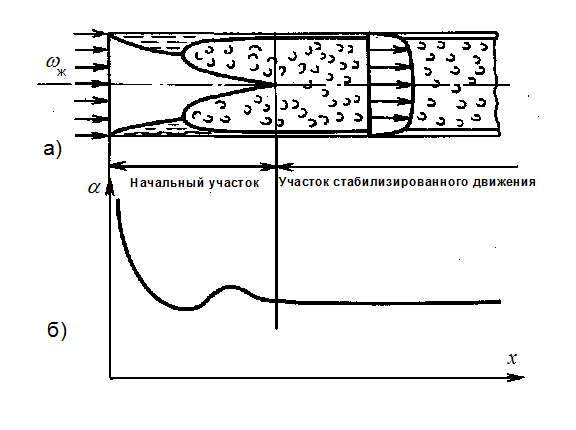
Рис. 9.3. Образование пограничного слоя (а) и распределение местного коэффициента теплоотдачи (б) при турбулентном течении теплоносителя внутри трубы.
Чтобы получить аналитическое выражение для коэффициента теплоотдачи, необходимо интегрировать систему дифференциальных уравнений, описывающих движение жидкости и перенос теплоты в ней. Даже при существенных упрощениях это возможно лишь в отдельных случаях при ламинарном течении жидкости, поэтому обычно для получения расчетных зависимостей прибегают к экспериментальному изучению явления.
Расчет свободной конвекции | Онлайн калькулятор
Процесс теплоотдачи при свободной конвекции широко распространен в технике. Конвекция, как физическое явление, происходит за счет переменной плотности в различных слоях жидкости или газа при изменении температуры. Для расчета теплоотдачи используется уравнение подобия вида:
Num = c×Ramn ;
где Ram – число Рэлея, причем за определяющую температуру для его расчета принята средняя температура пограничного слоя:
Tm = (Tп + Tс) / 2;
Определяющим размером в данном расчете является ширина или высота поверхности свободной конвекции, в зависимости от ее расположения.
Ниже представлен онлайн расчет свободной конвекции для горизонтальной и вертикальной плоской поверхности. Для расчета необходимо задать размеры поверхности, ее температуру, температуру рабочей среды, а так же характеристики рабочей среды для средней температуры пограничного слоя: динамическую вязкость, плотность, коэффициент объемного расширения, коэффициент теплопроводности и удельную теплоемкость.
Расчет свободной конвекции для горизонтальной поверхности
Для горизонтально расположенной поверхности реализована возможность выбора расположения поверхности – обращенной вверх или вниз.
Исходные данные:
A – длина поверхности, миллиметрах;
B – ширина поверхности, миллиметрах;
Tп – температура поверхности, в °C;
Tс – температура среды, в °C;
μ – динамическая вязкость теплоносителя, в паскаль×секунда;
ρ – плотность среды, в килограммах / метр3;
β – коэффициент объемного расширения среды, в °C -1;
λ – коэффициент теплопроводности среды, в ваттах / метр×°C×сек;
Cp – удельная теплоемкость среды, в джоулях / килограмм×°C.
Число Грасгофа:
Gr = g×B3×β×((Тп – Тc) / 2) / (μ / ρ)2;
Число Прандтля:
Pr = μ×Cp / λ;
Число Рэлея:
Ra = Gr×Pr;
Число Нуссельта:
Nu = c×Ran ;
Коэффициент теплоотдачи:
α = 1,3×Nu×λ / B – для поверхности теплообмена обращенной вверх;
α = 0,7×Nu×λ / B – для поверхности теплообмена обращенной вниз.
Расчет свободной конвекции для вертикальной поверхности
Для вертикально расположенной поверхности расчет проводится аналогично случаю горизонтального расположения с учетом поправочных коэффициентов.
Исходные данные:
A – высота поверхности, миллиметрах;
B – ширина поверхности, миллиметрах;
Tп – температура поверхности, в °C;
Tс – температура среды, в °C;
μ – динамическая вязкость среды, в паскаль×секунда;
ρ – плотность среды, в килограммах / метр3;
β – коэффициент объемного расширения среды, в °C -1;
λ – коэффициент теплопроводности среды, в ваттах / метр×°C×сек;
Cp – удельная теплоемкость среды, в джоулях / килограмм×°C.
ВОПРОС № 1 Теоретические основы теплоотдачи — Студопедия
Конвективный теплообмен
Литература:
1. Г.Д. Кавецкий, В.П. Касьяненко «Процессы и аппараты пищевой технологии».- М., КолосС, 2008.-591 с.: ил.
План лекции:
1. Теоретические основы теплоотдачи.
2. Связь коэффициента теплопередачи с коэффициентами теплоотдачи.
Контрольные вопросы:
1. Дайте определения и краткую характеристику существа процесса теплоотдачи?
2. В чем сущность основного закона теплоотдачи – закона Ньютона?
3. Какие критерии, характеризующие процесс теплоотдачи Вам известны?
4. Что каждый из них характеризует?
ВОПРОС № 1 Теоретические основы теплоотдачи
Теплоотдачей называется процесс теплообмена между поверхностью тела и окружающей средой.
Интенсивность теплоотдачи характеризуется коэффициентом теплоотдачи, равным отношению плотности теплового потока на поверхности раздела к температурному напору между поверхностью теплообмена и средой (теплоносителем).
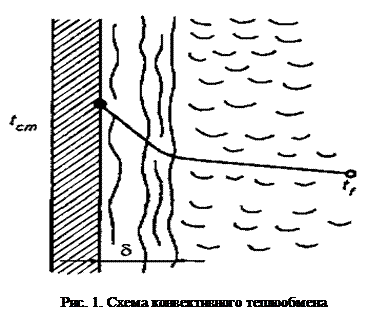
При конвективном теплообмене теплота распространяется в потоке жидкости или газа от поверхности твердого тела или к его поверхности одновременно конвекцией и теплопроводностью. От поверхности твердого тела к потоку жидкости она распространяется через пограничный слой за счет теплопроводности, от пограничного слоя к ядру потока жидкости или газа — в основном конвекцией. На интенсивность теплоотдачи существенное влияние оказывает характер движения потока жидкости или газа. Схема конвективного теплообмена приведена на рис. 1. Различают теплоотдачу при свободной и вынужденной конвекции. Под свободной, или естественной, конвекцией понимают перемещение частиц жидкости или газа в объеме аппарата или теплообменных устройств вследствие разности плотностей нагретых и холодных частиц жидкости или газа.
Скорость естественной конвекции определяется физическими свойствами жидкости или газа, разностью температур между горячими и холодными частицами и объемом, в котором протекает процесс.
Вынужденная, или принудительная, конвекция возникает под действием насоса или вентилятора и определяется физическими свойствами среды, скоростью ее движения, формой и размерами канала, в котором движется поток.
 |
При вынужденной конвекции теплообмен происходит значительно интенсивнее, чем при естественной.
Основной закон теплоотдачи — закон Ньютона гласит: количество теплоты dQ, переданное от поверхности теплообмена к потоку жидкости (газа) или от потока к поверхности теплообмена, прямо пропорционально площади поверхности теплообмена F, разности температур поверхности tст и ядра потока tf (или наоборот) и продолжительности процесса dτ:
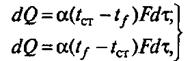
(1)
где α — коэффициент теплоотдачи, который показывает, какое количество теплоты передается от теплообменной поверхности в 1 м2 омывающему ее потоку или от потока поверхности теплообмена, равной 1 м2, в единицу времени (1 ч) при разности температур поверхности теплообмена и ядра потока 1 К.
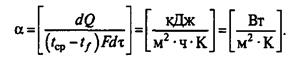 Единицу измерения коэффициента теплоотдачи можно получить, решив уравнения (1):
Единицу измерения коэффициента теплоотдачи можно получить, решив уравнения (1):
(2)
Если коэффициент теплоотдачи имеет постоянное значение вдоль всей поверхности теплообмена (а = const), уравнения (1) принимают вид
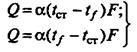 (3)
(3)
в зависимости от того, передается теплота от стенки омывающему стенку потоку или наоборот.
Значение коэффициента теплоотдачи, который определяет скорость конвективного теплообмена, зависит от многих факторов: режима движения жидкости (газа), физических параметров жидкости (газа), формы и размера поверхности теплообмена и др.
Коэффициент теплоотдачи рассчитывают по критериальных уравнениям, которые получают методами теории подобия из дифференциального уравнения конвективного теплообмена, дополненного уравнениями, характеризующими условие на границе раздела потока и стенки аппарата.
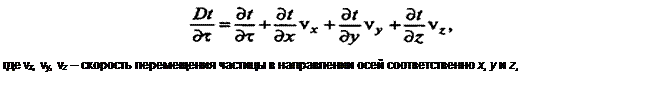 |
Дифференциальное уравнение конвективного теплообмена (уравнение Фурье—Кирхгофа) получают, приравняв субстанциональную производную* (4)
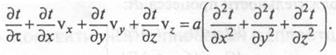 к уравнению (6):
к уравнению (6):
(5)
Для полного математического описания процесса последнее уравнение требуется дополнить условиями на границе раздела потока и стенки аппарата. Для этого рассмотрим процесс конвективного теплообмена между стенкой аппарата и потоком жидкости (см. рис. 1). В данном случае поток жидкости можно рассматривать как двухслойную систему, состоящую из пограничного слоя толщиной δ и ядра потока, в котором происходит интенсивное перемешивание частиц жидкости при турбулентном режиме.
Теплота от стенки аппарата через пограничный слой распространяется теплопроводностью, которая описывается законом Фурье [уравнение (5)]. Это же количество теплоты, описываемое законом Ньютона, распространяется в ядре потока. Приравнивая эти уравнения, получим уравнение, характеризующее условия на границе,
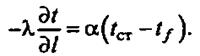 (6)
(6)
* Субстанциональная производная выражает изменение температуры элемента одновременно во времени и в пространстве, связанное с перемещением элемента из одной точки в другую.
Дифференциальные уравнения, однако, можно привести к расчетному виду только в простейших случаях. Во всех остальных случаях расчетные уравнения получают, используя методы теории подобия, из общих дифференциальных уравнений, приводя их при помощи экспериментальных данных к конкретному виду.
Критерий Нуссельта, характеризующий условия на границе, можно получить методами теории подобия из уравнения (6). Для этого делят обе части уравнения (6) на его левую часть и получают безразмерный комплекс
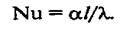 (7)
(7)
откуда после несложных преобразований — критерий Нуссельта
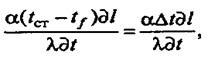 (8)
(8)
Критерий Фурье выводят из дифференциального уравнения конвективного теплообмена (5):
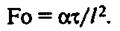 (9)
(9)
Критерий Фурье характеризует связь между скоростью изменения температурного поля, размерами канала, в котором происходит теплообмен, и физическими свойствами среды в нестационарных условиях.
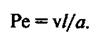 Критерий Пекле
Критерий Пекле
(10)
Критерий Пекле показывает соотношение между количеством теплоты, распространяемой в потоке жидкости или газа конвекцией, и теплопроводностью.
Легко видеть, что критерий Пекле представляет собой произведение критериев Рейнольдса и Прандтля
Ре = Vl/a = (Vl/v)(v/a) = RePr, (11)
где υ – кинематическая вязкость, м2/с.
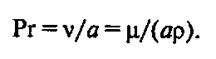 Критерий Прандтля характеризует поле теплофизических величин потока жидкости или газа
Критерий Прандтля характеризует поле теплофизических величин потока жидкости или газа
(12)
Учитывая, что коэффициент температуропроводности а = λ/сρ, критерий Прандтля записывается в виде Рг=μс/λ
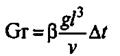 При теплообмене в условиях естественной конвекции в критериальные уравнения вводят критерии Грасгофа
При теплообмене в условиях естественной конвекции в критериальные уравнения вводят критерии Грасгофа
(13)
или Архимеда
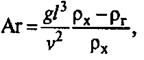
(14)
где β — температурный коэффициент объемного расширения жидкости или газа; v — кинематическая вязкость, м2/с; Δt — разность температур горячих и холодных частиц жидкости или газа, вызывающих естественную конвекцию частиц в среде, окружающей теплообменную поверхность; ρг и ρх — плотности соответственно горячей и холодной жидкости, кг/м3.
Из приведенных критериев подобия только критерий Нуссельта содержит искомый коэффициент теплоотдачи, не входящий в условия однозначности, поэтому он является определяемым критерием подобия.
Критериальное уравнение конвективного теплообмена в общем виде
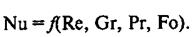
(15)
При стационарном процесса теплообмена из критериального уравнения (15) исключает критерий Фурье.
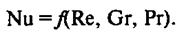
(16)
При вынужденной конвекции из критериального уравнения исключают критерий Грасгофа
Nu = f (Re, Pr) (17)
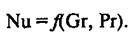 При естественной конвекции из критериального уравнения исключают критерий Рейнольдса
При естественной конвекции из критериального уравнения исключают критерий Рейнольдса
(18)
К расчетному виду уравнения (15), (17) и (18) приводят на основании экспериментальных данных, полученных в конкретной гидродинамической и геометрической обстановке.
Коэффициент теплоотдачи определяют по найденному из критериальных уравнений критерию Нуссельта.
Коэффициент теплоотдачи при естественной конвекции рассчитывают на основе критериального уравнения.
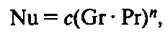
(19)
 в котором числовые значения сипвыбирают в зависимости от произведения GrPr:
в котором числовые значения сипвыбирают в зависимости от произведения GrPr:
Определяющей температурой в критерии Грасгофа является средняя температура пограничного слоя t= 0,5(tcт + tf),а Δt= tcт – t.
Коэффициент теплоотдачи при вынужденной конвекции теплоносителя в трубе определяют по следующим уравнениям:
для турбулентного режима (Re > 10 000)
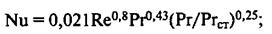 (20)
(20)
для ламинарного режима (Re ≤ 2320)
Nu = 0,17Re0,33Pr0,43Gr0,1(Pr\Prст)0,25, (21)
При поперечном обтекании трубы теплоносителем при Rе = (10÷2)∙105 используют уравнение
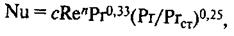 (22)
(22)
 В котором числовые значения с и п находят в зависимости от значения критерия Рейнольдса:
В котором числовые значения с и п находят в зависимости от значения критерия Рейнольдса:
Определяющим размером в этих уравнениях служит эквивалентный диаметр канала.
Физические параметры в критериях Nu, Re и Рr определены при средней температуре жидкости, а в критерии Рrст — при температуре стенки.
(Рr/Рrст)0,25 учитывает влияние на теплоотдачу направления теплового потока и температурного перепада.
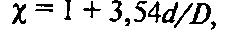 При расчете коэффициента теплоотдачи в змеевиках значение α, полученное по формуле (20), умножают на коэффициент χ, учитывающий размеры змеевика:
При расчете коэффициента теплоотдачи в змеевиках значение α, полученное по формуле (20), умножают на коэффициент χ, учитывающий размеры змеевика:
(23)
где d, D – соответственно внутренний диаметр трубы змеевика и диаметр витка змеевика, м.
Для воздуха формула (20) имеет вид
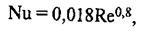 (24)
(24)
так как в этом случае Pr\Prст=1.
Когда теплота распространяется одновременно конвекцией и лучеиспусканием, в расчётное уравнение вводят общий коэффициент теплоотдачи αобщ= αк+ αизл, где αк – конвективный коэффициент теплоотдачи; αизл – коэффициент теплоотдачи излучением:
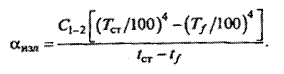 (25)
(25)
Тогда общее количество теплоты, отданное стенкой в единицу времени, Q = α общ (tст — tf)F.
Для определения общего коэффициента теплоотдачи [Вт/(м2 · К)] при расчете тепловых потерь аппаратуры, находящейся в закрытых помещениях, можно пользоваться приближенным уравнением
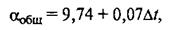 (26)
(26)
где Δt – разность температур поверхности стенки аппарата и окружающей среды.
ВОПРОС № 2 Связь коэффициента теплопередачи с коэффициентами теплоотдачи
Коэффициент теплопередачи рассчитывают на основании коэффициентов теплоотдачи, вычисленных по критериальным уравнениям.
Рассмотрим процесс теплопередачи между теплоносителями, разделенными стенкой (рис. 2). Пусть температура горячего теплоносителя tf1, холодного — tf2. Температуры поверхностей стенки соответственно tf1и tf2. Коэффициент теплоотдачи для горячего теплоносителя α1, холодного – α2.
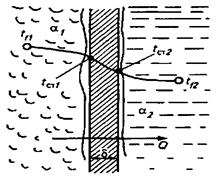
Рис. 2. К расчету процесса теплопередачи
При установившемся процессе количество теплоты Q, передаваемое в единицу времени через площадку F от ядра потока горячего теплоносителя стенке, равно количеству теплоты, передаваемому через стенку теплопроводностью и от стенки ядру потока холодного теплоносителя. Это количество теплоты можно определить:
по закону Ньютона Q = α1(tf1 — tст1) F;
по закону Фурье Q = λ/δ(tст1 – tст2) F;
по закону Ньютона Q = α2(tст2 — tf2)F.
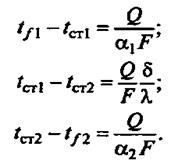 Из этих уравнений получают разности температур или частные температурные напоры.
Из этих уравнений получают разности температур или частные температурные напоры.
(36)
(37)
(38)
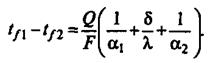 Складывая, левые и правые части этих уравнений, получают разность температур теплоносителей, или общий температурный напор
Складывая, левые и правые части этих уравнений, получают разность температур теплоносителей, или общий температурный напор
(39)
Отсюда
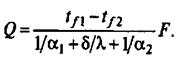
(40)
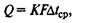 Из сопоставления уравнений и (40) получают
Из сопоставления уравнений и (40) получают
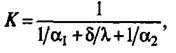
(41)
или
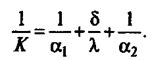
(42)
Величина 1/К, обратная коэффициенту теплопередачи, называется общим термическим сопротивлением теплопередачи и обозначается R(R= r1+ + rст + r2).
Величины l/α1 и 1/α2 называются частными термическими сопротивлениями r1 и r2, а δ/λ — термическим сопротивлением стенки rст. Из уравнения (42) следует, что общее термическое сопротивление теплопередаче равно сумме частных термических сопротивлений теплоотдаче теплоносителей и стенки.
В случае многослойной стенки в уравнение (42) вместо δ/λ подставляют сумму термических сопротивлений каждого слоя стенки. Тогда
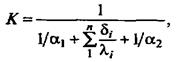
(43)
где п — число слоев стенки; і—порядковый номер слоя.
Отметим, что коэффициент теплопередачи всегда меньше минимального коэффициента теплоотдачи.
Основное уравнение теплопередачи и уравнение теплового баланса — Студопедия
Теплопередача. Теплоотдача
Теплота от одной среды к другой может передаваться при непосредственном контакте или через стенку.
Если теплота переходит от более нагретой среды к менее нагретой через разделяющую стенку, то процесс называется теплопередачей.
Если теплота переносится от стенки к среде (или наоборот), то процесс называется теплоотдачей.
В химической технологии теплообменные процессы осуществляются в аппаратуре, которая называется теплообменной аппаратурой.
Жидкости или газы, участвующие в теплообмене, называются рабочими средами.
Основной характеристикой теплообменного аппарата является поверхность теплообмена.
Связь между количеством теплоты передаваемым в аппарате и поверхностью теплообмена определяется основным кинетическим соотношением, которое называется о сновным уравнением теплопередачи:
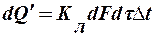 (1)
(1)
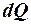 — количество переданного тепла, Дж;
— количество переданного тепла, Дж;
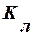 — локальный коэффициент теплопередачи между средами,
— локальный коэффициент теплопередачи между средами, 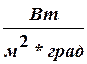 ;
;
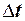 — разность температур между средами,0С;
— разность температур между средами,0С;
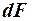 — элемент поверхности теплообмена, м2 ;
— элемент поверхности теплообмена, м2 ;
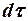 — время теплообмена, с
— время теплообмена, с
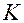 — коэффициент теплопередачи средний для всей поверхности,
— коэффициент теплопередачи средний для всей поверхности, 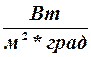 .
.
Физический смысл коэффициента теплопередачи:
Коэффициент теплопередачи показывает, какое количество теплоты в Дж переходит в 1с от более нагретого тела к менее нагретому через поверхность теплообмена в 1м2 при средней разности температур равной 1 град. Коэффициент теплопередачи определяет интенсивность теплообмена. Из основного уравнения теплопередачи (1) можно определить поверхность теплопередачи 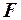 .
. 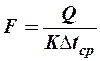 . (2)
. (2)
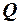 определяется из уравнения теплового баланса:
определяется из уравнения теплового баланса:
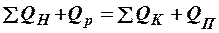 (3)
(3)
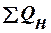 — потоки тепла, которые поступают в аппарат с исходными продуктами;
— потоки тепла, которые поступают в аппарат с исходными продуктами;
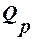 — теплота реакций ( теплота химических превращений; испарение жидкостей; выделение паров или газов из твердых поглотителей; теплота плавления и растворения). Для определения этих теплот используют справочные данные.
— теплота реакций ( теплота химических превращений; испарение жидкостей; выделение паров или газов из твердых поглотителей; теплота плавления и растворения). Для определения этих теплот используют справочные данные.
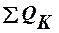 — потоки тепла, которые выходят из аппарата с конечными продуктами;
— потоки тепла, которые выходят из аппарата с конечными продуктами;
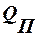 — потери тепла в окружающую среду (» 3¸5%).
— потери тепла в окружающую среду (» 3¸5%).
Теплопроводность
Закон Фурье (установлен опытным путем) – количество теплоты 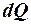 переданного теплопроводностью, прямо пропорционально градиенту температуры
переданного теплопроводностью, прямо пропорционально градиенту температуры 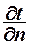 , времени
, времени 
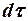 и площади сечения
и площади сечения 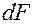 , перпендикулярного направлению теплового потока:
, перпендикулярного направлению теплового потока:
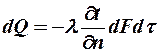 , (4)
, (4)
— коэффициент теплопроводности, Вт/м?град.
Коэффициент теплопроводности l показывает, какое количество теплоты в Дж проходит в 1с через 1м2 поверхности при разности температур в 10 на единицу длины нормали к изотермической поверхности. (Изотермическая поверхность — геометрическое место точек с одинаковой температурой).
Плотность теплового потока 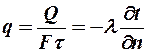 . (5)
. (5)
( ²-² означает что тепло перемещается в сторону падения температуры).
Дифференциальное уравнение теплопроводности
Процесс распространения теплоты теплопроводностью математически описывается дифференциальным уравнением, выведенным на основе закона сохранения энергии.
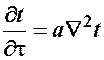 ; (6) –
; (6) –
Дифференциальное уравнение теплопроводности в неподвижной среде . 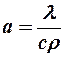 — коэффициент температуропроводности; характеризует теплоинерционные свойства вещества. Чем больше
— коэффициент температуропроводности; характеризует теплоинерционные свойства вещества. Чем больше 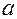 , тем тело быстрее охлаждается (нагревается).
, тем тело быстрее охлаждается (нагревается).
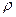 ,
,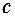 ,
,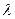 — не изменяются по направлению и во времени.
— не изменяются по направлению и во времени.
Для стационарных процессов —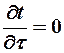 ,т.е. температура не меняется со временем и уравнение (6) принимает вид
,т.е. температура не меняется со временем и уравнение (6) принимает вид 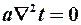 .Т.к. а¹0, то
.Т.к. а¹0, то 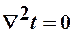 (7)
(7)
или 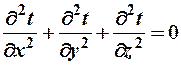 — Дифференциальное уравнение теплопроводности в неподвижной среде при стационарном тепловом режиме. Уравнения (6) и (7) дают возможность решать задачи связанные с распространением тепла в теле путем теплопроводности как при стационарном, так и при нестационарном тепловом режиме. При решении конкретных задач уравнения дополняются соответствующими начальными и граничными условиями.
— Дифференциальное уравнение теплопроводности в неподвижной среде при стационарном тепловом режиме. Уравнения (6) и (7) дают возможность решать задачи связанные с распространением тепла в теле путем теплопроводности как при стационарном, так и при нестационарном тепловом режиме. При решении конкретных задач уравнения дополняются соответствующими начальными и граничными условиями.
Теплопроводность плоской стенки
В инженерной практике часто встречаются задачи стационарной теплопроводности через плоскую и цилиндрическую стенки. Это задачи расчета тепловой изоляции аппаратов и трубопроводов.
Стенка состоит из однородного материала; d — толщина стенки;l — теплопроводность материала стенки; tст1, tст2 – температура стенки. tст1 > tст2.
Вывод уравнения теплопроводности плоской стенки
Запишем уравнение Фурье в развернутом виде
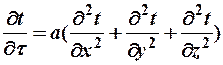
При стационарном режиме температура в различных точках постоянна во времени, т.е
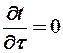
Температурное поле одномерно (плоская стенка) 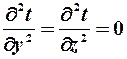 .
.
Т.о. уравнение Фурье приобретает вид:  d2t/dx2=0.
d2t/dx2=0.
Проинтегрируем дважды: dt/dx = C1; t = C1x+C2. C1 и С2 найдем из условий на границе: х=0; х=d. При х=0 tст1=С2, а при х=d tст2= C1d+ tст1;
C1= ( tст2— tст1)/d; В результате получим
t=x(tст2— tст1)/d+ tст1 (8)
Температура по толщине стенки х меняется линейно, температурный градиент сохраняет постоянное значение. Подставим полученное значение градиента температуры в (4)-з. Фурье и получим уравнение теплопроводности плоской стенки при стационарном тепловом режиме
dQ=l/d( tст1 — tст2)dFdt .
Q=l/d( tст 1 — tст2)Ft (9).
Здесь l/d — термическая проводимость стенки.
Теплопроводность цилиндрической стенки (самост.)
В тепловых процессах одновременно с теплопроводностью и конвекцией почти всегда имеет место тепловое излучение, причем, чем выше температура тела, тем больше тепла оно передает в виде теплового излучения.
Тепловое излучение
— это процесс распространения энергии в форме электромагнитных волн.
Конвективная теплопередача
Тепловая энергия, передаваемая между поверхностью и движущейся жидкостью с разными температурами — известна как конвекция .
На самом деле это комбинация диффузии и объемного движения молекул. Вблизи поверхности скорость жидкости мала, и преобладает диффузия. На расстоянии от поверхности объемное движение усиливает влияние и преобладает.
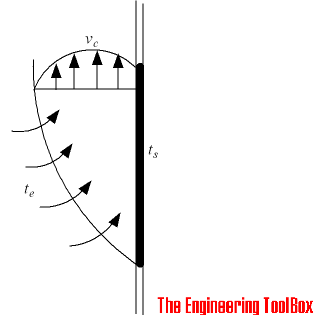
Конвективная теплопередача может быть
- принудительной или вспомогательной конвекцией
- естественной или свободной конвекцией
принудительной или вспомогательной конвекцией
принудительной конвекцией, когда поток жидкости вызван внешняя сила, такая как насос, вентилятор или смеситель.
Естественная или свободная конвекция
Естественная конвекция вызывается выталкивающими силами из-за разницы плотности, вызванной колебаниями температуры в жидкости. При нагревании изменение плотности в пограничном слое заставит жидкость подниматься и заменяться более холодной жидкостью, которая также будет нагреваться и подниматься. Это продолжающееся явление называется свободной или естественной конвекцией.
Процессы кипения или конденсации также называют конвективными процессами теплопередачи.
- Теплопередача на единицу поверхности за счет конвекции была впервые описана Ньютоном, и это соотношение известно как закон охлаждения Ньютона .
Уравнение конвекции может быть выражено как:
q = h c A dT (1)
, где
q = теплопередача за единицу времени (Вт, БТЕ / ч)
A = площадь теплопередачи поверхности (м 2 , футы 2 )
h c = коэффициент конвективной теплопередачи процесса ( Вт / (м 2o C, Btu / (фут 2 h o F) )
dT = разница температур между поверхностью и основной жидкостью ( o C, F)
Коэффициенты теплопередачи — единицы
Коэффициенты конвективной теплопередачи
Коэффициенты конвективной теплопередачи — ч c — в зависимости от t тип среды, будь то газ или жидкость, и свойства потока, такие как скорость, вязкость и другие свойства, зависящие от потока и температуры.
Типичные коэффициенты конвективной теплопередачи для некоторых распространенных применений потока жидкости:
- Свободная конвекция — воздух, газы и сухие пары: 0,5 — 1000 (Вт / (м 2 K))
- Свободная конвекция — вода и жидкости: 50 — 3000 (Вт / (м 2 K))
- Принудительная конвекция — воздух, газы и сухие пары: 10 — 1000 (Вт / (м 2 K))
- Принудительная конвекция — вода и жидкости: 50 — 10000 (Вт / (м 2 K))
- Принудительная конвекция — жидкие металлы: 5000 — 40000 (Вт / (м 2 K))
- Кипящая вода: 3.000 — 100,000 (Вт / (м 2 K))
- Водяной пар конденсата: 5.000 — 100,000 (Вт / (м 2 K))
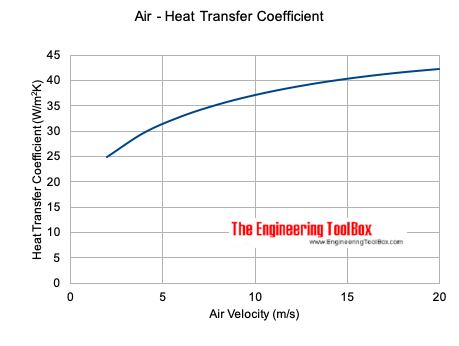
Коэффициент конвективной теплопередачи для воздуха
Коэффициент конвективной теплопередачи для потока воздуха может быть приблизительно равен
ч c = 10,45 — v + 10 v 1/2 (2)
, где
h c = коэффициент теплопередачи (кКал / м 2 ч ° C)
v = относительная скорость между поверхностью объекта и воздухом (м / с)
Начиная с
1 ккал / м 2 ч ° С = 1.16 Вт / м 2 ° C
— (2) можно изменить на
h cW = 12,12 — 1,16 v + 11,6 v 1/2 (2b)
где
ч cW = коэффициент теплопередачи (Вт / м 2 ° C )
Примечание! — это эмпирическое уравнение, которое может использоваться для скоростей от 2 до 20 м / с .
Пример — конвективная теплопередача
Жидкость течет по плоской поверхности 1 м на 1 м. Температура поверхности 50 o C , температура жидкости 20 o C и коэффициент конвективной теплопередачи 2000 Вт / м 2o С . Конвективную теплопередачу между более горячей поверхностью и более холодным воздухом можно рассчитать как
q = (2000 Вт / (м 2o C)) ((1 м) (1 м)) ((50 o C) — (20 o C))
= 60000 (Вт)
= 60 (кВт)
Калькулятор конвективной теплопередачи
Таблица конвективной теплопередачи
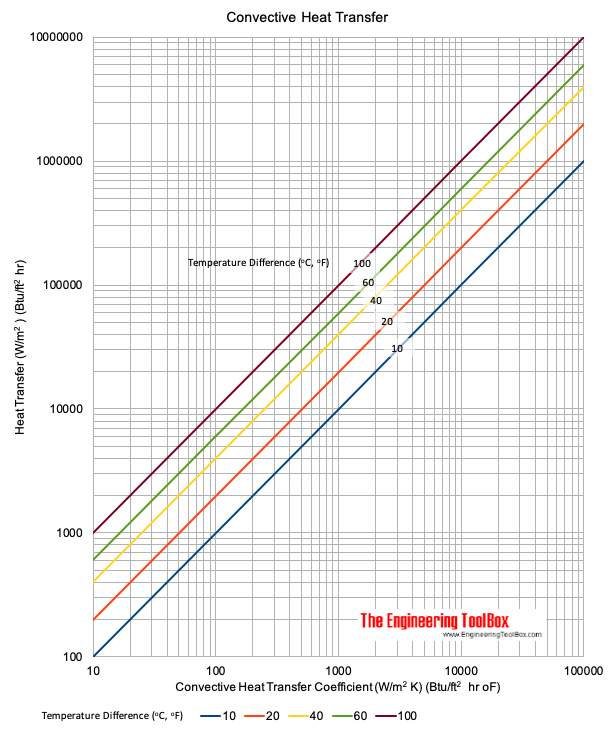
.
Общий коэффициент теплопередачи
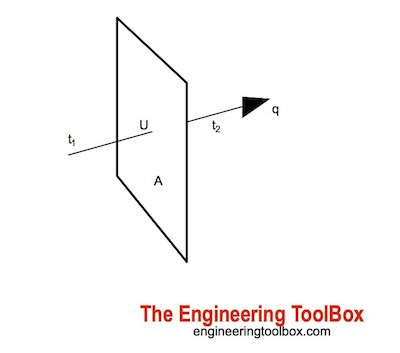
Теплопередача через поверхность, например стену, может быть рассчитана как
q = UA dT (1)
, где
q = теплопередача (Вт (Дж / с), БТЕ / ч)
U = общий коэффициент теплопередачи (Вт / (м 2 K), БТЕ / (фут 2 ч o F) )
A = площадь стены (м 2 , фут 2 )
dT = (t 1 — t 2 )
= разница температур по стене ( o C, o F)
Общий коэффициент теплопередачи для многослойной стены, трубы или теплообменника — с потоком жидкости с каждой стороны стены — можно рассчитать как
1 / UA = 1 / ч ci A i + Σ (s 9004 5 n / k n A n ) + 1 / h co A o (2)
где
U = общий коэффициент теплопередачи (Вт / (м 2 K), БТЕ / (фут 2 ч o F) )
k n = теплопроводность материала в слое n (Вт / (м · K), БТЕ / (час · фут · ° F) )
h ci, o = внутренняя или внешняя стенка индивидуальная жидкость конвекция коэффициент теплопередачи (Вт / (м 2 K), Btu / (фут 2 h o F) )
s n = толщина слоя n ( м, футы)
9 0002 Плоская стена с равной площадью во всех слоях — можно упростить до
1 / U = 1 / h ci + Σ (s n / k n ) + 1 / h co (3)
Теплопроводность — k — для некоторых типичных материалов (проводимость не зависит от температуры)
- Полипропилен PP: 0.1 — 0,22 Вт / (м · К)
- Нержавеющая сталь: 16 — 24 Вт / (м · К)
- Алюминий: 205 — 250 Вт / (м · К)
Преобразовать между Метрические и имперские единицы
- 1 Вт / (м · К) = 0,5779 БТЕ / (фут · ч o F)
- 1 Вт / (м 2 K) = 0,85984 ккал / (hm 2 o C) = 0,1761 Btu / (ft 2 h o F)
Коэффициент конвективной теплопередачи — h — зависит от
- тип жидкости — газ или жидкость
- свойства потока, такие как скорость
- другие свойства, зависящие от потока и температуры
Коэффициент конвективной теплопередачи для некоторых распространенных жидкостей:
- Воздух — от 10 до 100 Вт / м 2 K
- Вода — 500 до 10 000 Вт / м 2 K
Многослойные стены — Калькулятор теплопередачи
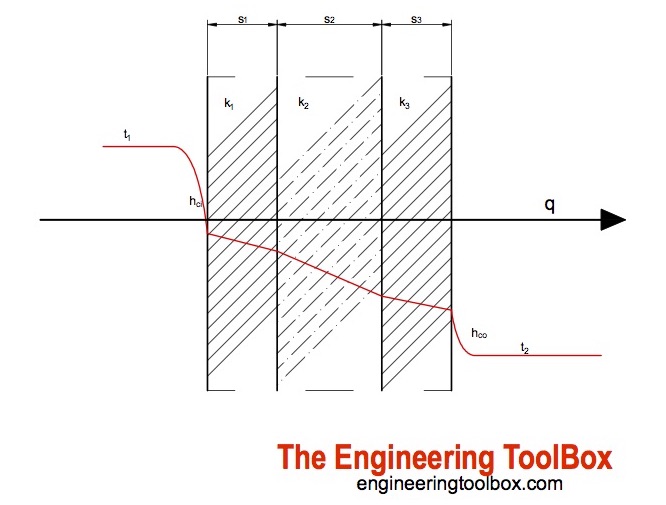
Этот калькулятор можно использовать для расчета общего коэффициента теплопередачи и теплопередачи через многослойную стену.Калькулятор является универсальным и может использоваться для метрических или британских единиц при условии, что единицы используются последовательно.
A — площадь (м 2 , футов 2 )
t 1 — температура 1 ( o C, o F)
t 2 — температура 2 ( o C, o F)
h ci — коэффициент конвективной теплоотдачи внутри стенки (Вт / (м 2 K), БТЕ / ( ft 2 h o F) )
s 1 — толщина 1 (м, фут) k 1 — теплопроводность 1 (Вт / (м K) , БТЕ / (ч · фут · ° F) )
с 2 — толщина 2 (м, фут) k 2 — теплопроводность 2 (Вт / (м · К), Британские тепловые единицы / (час · фут · ° F) )
с 3 — толщина 3 (м, фут) k 3 — теплопроводность 3 (Вт / (м · K), БТЕ / (час · фут · ° F) )
h co — коэффициент конвективной теплопередачи снаружи стены ( Вт / (м 2 K), БТЕ / (фут 2 h o F) )
Тепловое сопротивление теплопередачи
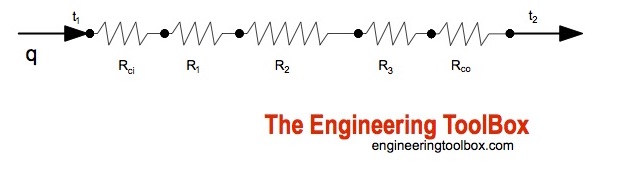
Сопротивление теплопередаче может быть выражено как
R = 1 / U (4)
где
R = сопротивление теплопередаче (м 2 K / W, ft 2 h ° F / BTU)
Стена разделена на участки термического сопротивления, где
- теплопередача между жидкостью и стеной — это одно сопротивление
- сама стена является одним сопротивлением
- передача между стенкой l, а вторая жидкость представляет собой тепловое сопротивление
Поверхностные покрытия или слои «обожженного» продукта добавляют дополнительное тепловое сопротивление стенкам, снижая общий коэффициент теплопередачи.
Некоторые типичные сопротивления теплопередаче
- статический слой воздуха, 40 мм (1,57 дюйма) : R = 0,18 м 2 K / Вт
- внутреннее сопротивление теплопередаче, горизонтальный ток: R = 0,13 м 2 K / W
- внешнее сопротивление теплопередаче, горизонтальный ток: R = 0,04 м 2 K / W
- внутреннее сопротивление теплопередаче, тепловой ток снизу вверх: R = 0,10 м 2 K / W
- внешнее сопротивление теплопередаче, тепловой ток сверху вниз: R = 0.17 м 2 K / W
Пример — теплопередача в теплообменнике воздух-воздух
Пластинчатый теплообменник воздух-воздух площадью 2 м 2 и толщиной стенки 0,1 мм может быть изготовлен в полипропилен PP, алюминий или нержавеющая сталь.
Коэффициент конвекции тепла для воздуха составляет 50 Вт / м 2 K . Температура внутри теплообменника 100 o C , а наружная температура 20 o C .
Общий коэффициент теплопередачи U на единицу площади можно рассчитать, изменив (3) на
U = 1 / (1 / h ci + s / k + 1 / h co ) (3b)
Общий коэффициент теплопередачи для теплообменника из полипропилена
- с теплопроводностью 0,1 Вт / мК составляет
U PP = 1 / (1 / ( 50 Вт / м 2 K ) + ( 0.1 мм ) (10 -3 м / мм) / ( 0,1 Вт / мK ) + 1/ ( 50 Вт / м 2 K ) )
= 24,4 Вт / м 2 K
Теплопередача
q = ( 24,4 Вт / м 2 K ) ( 2 м 2 ) (( 100 o C ) — (2 0 o C ))
= 3904 W
= 3.9 кВт
- нержавеющая сталь с теплопроводностью 16 Вт / м · К :
U SS = 1 / (1 / ( 50 Вт / м 2 K ) + ( 0,1 мм ) (10 -3 м / мм) / ( 16 Вт / мK ) + 1/ ( 50 Вт / м 2 K ) )
= 25 Вт / м 2 K
Теплопередача
q = ( 25 Вт / м 2 K ) ( 2 м 2 ) (( 100 o C ) — (2 0 o C ))
= 4000 Вт
= 4 кВт
- алюминий с теплопроводностью 205 Вт / мK :
U Al = 1 / (1 / ( 50 Вт / м 2 K 90 077) + ( 0.1 мм ) (10 -3 м / мм) / (205 Вт / мK ) + 1/ ( 50 Вт / м 2 K ) )
= 25 Вт / м 2 K
Теплопередача
q = ( 25 Вт / м 2 K ) ( 2 м 2 ) (( 100 o C ) — (2 0 o C ))
= 4000 Вт
= 4 кВт
- 1 Вт / (м 2 К) = 0.85984 ккал / (hm 2 o C) = 0,1761 Btu / (ft 2 h o F)
Типичный общий коэффициент теплопередачи
- Газ свободной конвекции — газ свободной конвекции: U = 1-2 Вт / м 2 K (стандартное окно, воздух из помещения через стекло)
- Газ без конвекции — принудительная жидкая (проточная) вода: U = 5-15 Вт / м 2 K (типовые радиаторы центрального отопления)
- Свободная конвекция газа — конденсирующийся пар Вода: U = 5-20 Вт / м 2 K (типовые паровые радиаторы)
- Принудительная конвекция (проточная) Газ — Свободная конвекция газ: U = 3-10 Вт / м 2 K (пароперегреватели)
- Принудительная конвекция (проточный) Газ — Принудительная конвекция Газ: U = 10-30 Вт / м 2 K (газы теплообменника)
- Принудительная конвекция (проточный) газ — Принудительная жидкая (проточная) вода: U = 10-50 Вт / м 2 9 0022 K (газовые охладители)
- Принудительная конвекция (проточный) Газ — конденсирующийся пар Вода: U = 10-50 Вт / м 2 K (воздухонагреватели)
- Безжидкостная конвекция — принудительная конвекция Газ: U = 10-50 Вт / м 2 K (газовый котел)
- Жидкостная конвекция — свободная конвекция Жидкость: U = 25-500 Вт / м 2 K (масляная баня для отопления)
- Без жидкости Конвекция — принудительный ток жидкости (вода): U = 50 — 100 Вт / м 2 K (нагревательный змеевик в воде в резервуаре, вода без рулевого управления), 500-2000 Вт / м 2 K (нагревательный змеевик в резервуарной воде) , вода с рулевым управлением)
- Конвекция без жидкости — Конденсирующийся пар воды: U = 300 — 1000 Вт / м 2 K (паровые рубашки вокруг сосудов с мешалками, вода), 150 — 500 Вт / м 2 K (другие жидкости)
- Принудительная жидкость (текущая) вода — газ свободной конвекции: U = 10-40 Вт / м 2 K (горючий камера + излучение)
- Принудительная жидкость (текущая) вода — Свободная конвекционная жидкость: U = 500 — 1500 Вт / м 2 K (охлаждающий змеевик — перемешиваемый)
- Принудительная жидкость (текущая) вода — Принудительная жидкость (проточная вода): U = 900 — 2500 Вт / м 2 K (теплообменник вода / вода)
- Принудительная жидкая (проточная) вода — Конденсирующий пар водяной: U = 1000 — 4000 Вт / м 2 K (конденсаторы водяного пара)
- Кипящая жидкая вода — свободный конвекционный газ: U = 10-40 Вт / м 2 K (паровой котел + излучение)
- Кипящая жидкая вода — принудительное течение жидкости (вода) : U = 300 — 1000 Вт / м 2 K (испарение холодильников или охладителей рассола)
- Кипящая жидкая вода — Конденсирующий пар воды: U = 1500 — 6000 Вт / м 2 K (испарители пар / вода)
,Таблица коэффициентов конвективной теплопередачи
| Инженеры Edge
Связанные ресурсы: теплопередача
Таблица коэффициентов конвективной теплопередачи
Теплообменная техника
Термодинамика
Таблица коэффициентов конвективной теплопередачи
В следующей таблице представлены типичные коэффициенты конвективной конвективной теплопередачи для жидкостей и конкретных применений
Типовые значения коэффициента теплопередачи
| Тип потока | (Вт / м 2 K) |
| Принудительная конвекция; низкоскоростной поток воздуха над поверхностью | 10 |
| Принудительная конвекция; умеренная скорость потока воздуха над поверхностью | 100 |
| Принудительная конвекция; умеренная скорость перетока воздуха через цилиндр | 200 |
| Принудительная конвекция; умеренный поток воды в трубе | 3000 |
| принудительная конвекция; расплавленные металлы | от 2000 до 45000 |
| Принудительная конвекция; кипяток в трубе | 50 000 |
| Принудительная конвекция — вода и жидкости | от 50 до 10000 |
| Свободная конвекция — газы и сухие пары | 5 до 37 |
| Свободная конвекция — вода и жидкости | от 50 до 3000 |
| Воздух | от 10 до 100 |
| Свободная конвекция; вертикальная пластина на воздухе с перепадом температур 30 ° C | 5 |
| Кипяток | 3.От 000 до 100 000 |
| Водопровод в трубах | от 500 до 1200 |
| Водяной конденсат | 5,0 — 100,0 |
| Вода в условиях свободной конвекции | от 100 до 1200 |
| Масло в свободной конвекции | от 50 до 350 |
| Расход газа по трубкам и между трубками | от 10 до 350 |
Типовые значения коэффициентов теплопередачи нагревателей
Нагреватели (без фазового перехода) коэффициенты теплопередачи | ||
| Горячая жидкость | Холодная жидкость | (БТЕ / час-фут 2 -F) |
| Пар | Воздух | 10–20 |
| Пар | Вода | 250–750 |
| Пар | Метанол | 200–700 |
| Пар | Аммиак | 200–700 |
| Пар | Водные растворы | 100–700 |
| Пар | Легкие углеводороды (вязкость <0.5 сП) | 100–200 |
| Пар | Углеводороды средние (0,5 сП <вязкость <1 сП) | 50–100 |
| Пар | Углеводороды тяжелые (вязкость> 1) | 6–60 |
| Пар | Газы | 5–50 |
| Даутерм | Газы | 4-40 |
| Даутерм | Тяжелые масла | 8–60 |
| Дымовой газ | Ароматический углеводород и пар | 5–10 |
Типовые значения коэффициентов теплопередачи испарителя
Коэффициенты теплопередачи испарителей | ||
| Горячая жидкость | Холодная жидкость | Общий U (БТЕ / час-фут 2 -F) |
| Пар | Вода | 350–750 |
| Пар | Растворители органические | 100–200 |
| Пар | Легкие масла | 80–180 |
| Пар | Тяжелые масла (вакуум) | 25–75 |
| Вода | Хладагент | 75–150 |
| Органические растворители | Хладагент | 30–100 |
Типовые значения коэффициентов теплопередачи охладителей
Охладители (без фазового перехода) коэффициенты теплопередачи | ||
| Холодная жидкость | Горячая жидкость | Общий U (БТЕ / час-фут 2 -F) |
| Вода | Вода | 150–300 |
| Вода | Органический растворитель | 50–150 |
| Вода | Газы | 3–50 |
| Вода | Легкие масла | 60–160 |
| Вода | Тяжелые масла | 10–50 |
| Дизельное топливо | Органический растворитель | 20–70 |
| рассол | Вода | 100–200 |
| рассол | Органический растворитель | 30–90 |
| рассол | Газы | 3–50 |
| Органические растворители | Растворители органические | 20–60 |
| Тяжелые масла | Тяжелые масла | 8–50 |
Типовые значения коэффициентов теплопередачи конденсаторов
Коэффициенты теплопередачи конденсаторов | ||
| Холодная жидкость | Горячая жидкость | Общий U (БТЕ / час-фут 2 -F) |
| Вода | Пар (давление) | 350-750 |
| Вода | Пар (вакуум) | 300–600 |
| Вода или рассол | Органический растворитель (насыщенный, атмосферный) | 100–200 |
| Вода или рассол | Органический растворитель (атмосферный, неконденсирующийся) | 20–80 |
| Вода или рассол | Органический растворитель (насыщенный, вакуум) | 50–120 |
| Вода или рассол | Органический растворитель (вакуум, неконденсирующиеся с высокой концентрацией) | 10–50 |
| Вода или рассол | Ароматические пары (атмосферные, неконденсирующиеся) | 5–30 |
| Вода | Углеводород низкокипящий (атмосферный) | 80–200 |
| Вода | Высококипящий углеводород (вакуум) | 10–30 |
Связанный:
 |

© Copyright 2000-2020, Engineers Edge, LLC www.engineeringsedge.com
Все права защищены
Отказ от ответственности
| Обратная связь | реклама
| Контакты
Дата / Время:
,
КОЭФФИЦИЕНТ ТЕПЛОПЕРЕДАЧИ
Коэффициент теплопередачи — это количественная характеристика конвективной теплопередачи между текучей средой (текучей средой) и поверхностью (стенкой), через которую она протекает. Эта характеристика появляется как коэффициент пропорциональности а в соотношении Ньютона-Рихмана
где — плотность теплового потока на стенке, T w — температура стенки, T t — характерная температура жидкости, например, температура T e вдали от стенки во внешнем потоке, температура объемного потока T б в тубах и др.Единица измерения в международной системе единиц (СИ) (см. Международная система единиц) — Вт / (м 2 K), 1 Вт / (м 2 K) = 0,86 ккал / (м 2 ч ° C) = 0,1761 британских тепловых единиц / (hft 2 ° F) или 1 ккал / (m 2 час ° C) = 1,1630 Вт / (m 2 K), 1 британских тепловых единиц / (hft 2 ° F) = 5,6785 Вт / (м 2 К). Коэффициент теплопередачи получил широкое распространение при расчетах конвективной теплопередачи и при решении задач внешнего теплообмена между теплопроводной твердой средой и ее окружением.Коэффициент теплопередачи зависит как от тепловых свойств среды, гидродинамических характеристик ее потока, так и от гидродинамических и тепловых граничных условий. Используя методы теории подобия, зависимость коэффициента теплоотдачи от многих факторов может быть представлена во многих практически важных случаях в виде компактных соотношений между безразмерными параметрами, известных как критерии подобия. Эти отношения называются обобщенными уравнениями (формулами) или подобием. Число Нуссельта Nu = αl / λf или число Стентона St = используется в качестве безразмерного числа для теплопередачи в этих уравнениях, где 1 — характерный размер поверхности в потоке, массовая скорость потока жидкости, λ . f и C pf теплопроводность и теплоемкость жидкости.При решении задач теплопроводности в твердом теле распределение коэффициента теплопередачи α между телом и его окружением часто задается как граничное условие. Здесь полезно использовать безразмерный независимый параметр, число Био Bi = αl / λ s , где λ s — теплопроводность твердого тела, а 1 — его характерный размер. Зависимость чисел Nu и St от чисел Re и Pr играет существенную роль в теплообмене за счет принудительной конвекции.В случае полностью развитой теплопередачи в круглой трубе с ламинарным потоком жидкости число Нуссельта является постоянной величиной, а именно Nu = 3,66 при постоянной температуре стенки и 4,36 при постоянном тепловом потоке (см. Трубы (однофазная теплопередача в) ). В случае свободной конвекции число Nu зависит от чисел Gr и Pr. Когда теплоемкость жидкости существенно меняется, коэффициент теплопередачи часто определяется в терминах разницы энтальпий (h w — h f ).Понятие коэффициента теплоотдачи используется также при теплообмене с фазовыми превращениями в жидкости (кипение, конденсация). В этом случае температура жидкости характеризуется температурой насыщения T s . Порядок величины коэффициента теплоотдачи для разных случаев теплообмена представлен в таблице 1.
При анализе внутренней теплопередачи в пористых телах, т. Е. Конвективной теплопередачи между жесткой матрицей и проникающей через нее жидкостью, часто используется объемный коэффициент теплопередачи.
где qv — тепловой поток, проходящий от жесткой матрицы к жидкости в единице объема пористого тела, T w — локальная температура матрицы, а T f — локальная объемная температура жидкости.
Следует подчеркнуть, что постоянство α в широком диапазоне и ΔT (при прочих равных условиях) встречается только в случае конвективного теплообмена, когда физические свойства жидкости изменяются незначительно при теплопередаче. При конвективном переносе тепла в жидкости с различными свойствами и при кипении коэффициент теплопередачи может существенно зависеть от и ΔT. В этих случаях увеличение теплового потока может вызвать опасные явления, такие как выгорание (переходный тепловой поток) и ухудшение турбулентной теплопередачи в трубках.Если (ΔT) является нелинейным, представляется неуместным представлять его в терминах коэффициента α при анализе, например, устойчивости к кипению.
Общий коэффициент теплопередачи
где T f1 и T f2 — температуры нагреваемой и нагретой жидкостей, используется при расчетах теплопередачи между двумя жидкостями через разделительную стенку. Значения U для наиболее часто используемых конфигураций стен определяются по формулам
для плоской многослойной стены,
для цилиндрической многослойной стенки, и
для сферической многослойной стены.
Здесь D 1 и D 2 — это внутренний и внешний диаметры стены, D — эталонный диаметр, по которому определяется эталонная поверхность теплопередачи, S i , D i , D i + 1 и λ i — толщина, внутренний и внешний диаметры, а также теплопроводность i-го слоя. Первый и третий члены в скобках называют тепловыми сопротивлениями теплопередачи. Для их опускания стены оребрены оребрением и используются различные методы увеличения теплоотдачи.Второй член в скобках означает тепловое сопротивление стены, которое может значительно увеличиться в результате загрязнения стены, например накипи и образования золы, или плохой теплопередачи между слоями стены. Значения α и U для малого элемента теплопередающей поверхности называются локальными. Если они не сильно различаются, то при практических расчетах теплоотдачи на поверхностях конечных размеров используются средние значения коэффициентов и уравнение теплопередачи
где A — эталонная поверхность теплопередачи и (часто среднее логарифмическое) падение температуры (см. среднюю разность температур).
Таблица 1. Ориентировочные значения коэффициента теплопередачи
ССЫЛКИ
Якоб М. (1958) Теплопередача , Вили, Нью-Йорк, Чепмен и Холл, Лондон.
Schneider, P. J. (1955) Conduction Heat Transfer , Addison-Wesley Publ. Co., Кембридж.
Adiutory, E. F. (1974) The New Heat Transfer, vols. 1,2, Ventuno Press, Цинциннати.
.
