Расчет площади радиатора: Расчёт радиаторов для транзисторов и микросхем. Онлайн калькулятор теплоотводов.
Расчёт радиаторов для транзисторов и микросхем. Онлайн калькулятор теплоотводов.
— На кой хрен козе баян? Она и так весёлая … — живо интересовались удмуртские радиолюбители, разглядывая диковинный
теплоотвод, установленный на лампу выходного каскада.
— Только для игры на баяне, козе баян и нужен, на какой же ещё? — гордо отвечал владелец теплоотвода, весьма довольный
произведённым на коллег впечатлением.
На самом деле, вакуумным приборам, работающим в штатном режиме, дополнительный отвод тепла не требуется.
А вот мощным транзисторам, микросхемам и всяким диодам, которые толком и на баяне играть не умеют
и, подобно лампам, рассеивать тепловую мощность путём естественной конвекции не научились — подавай принудительный отвод тепла от
кристалла полупроводника. А не подашь, отойдут стройными рядами от мира сего из-за перегрева и последующего разрушения этого самого
рабочего кристалла.
Так вот, для обеспечения эффективного отвода тепла от силового элемента и применяют теплоотводы (радиаторы).
Полный расчёт радиатора — вещь кропотливая. Можно воспользоваться грубым расчётом —
для рассеивания 1 ватта тепла, выделяемого полупроводниковым прибором, достаточно использовать площадь теплоотвода,
равную 30 квадратным сантиметрам.
Но лучше воспользоваться специальной программой.
Существует формула для расчёта теплового сопротивления теплоотвода:
Q=(T2-T1)/P-Q1-Q2, где
Т2 — максимальная температура кристалла транзистора по справочнику,
Т1 — максимально допустимая температура в коробке с нашим устройством,
P — рассеиваемая на транзисторе мощность,
Q1 — тепловое сопротивление кристалл-корпус по справочнику,
Q2 — тепловое сопротивление корпус-радиатор.
Эта формула непререкаема и не должна вызывать никаких сомнений.
А вот формулы по переводу рассчитанного теплового сопротивления в площадь поверхности радиатора, выуженные из нашей справочной литературы —
не вызвали чувства глубокого удовлетворения, в связи с существенным несоответствием получаемых результатов суровой реальности жизни.
Пришлось искать правду в источниках империалистических агрессоров, а конкретно — в рекомендациях по выбору алюминиевых радиаторов
американской фирмы Aavid Thermalloy.
Информация эта неожиданно обнаружилась в электротехническом справочнике г-на Корякина-Черняка С. Л., за что ему большое человеческое
спасибо.
Теперь давайте определимся с терминологией.
S — площадь поверхности радиатора, равная удвоенной суммарной площади основания радиатора и всех площадей рёбер радиатора.
Почему удвоенной? Потому, что и основание, и все рёбра теплоотвода имеют по две поверхности, которыми и излучают тепло
в окружающее пространство.
Q — тепловое сопротивление между радиатором и окружающей средой. Спецификация большинства радиаторов содержит этот
параметр.
Q1 — тепловое сопротивление между кристаллом и корпусом силовых элементов обычно приводится в справочнике
и обозначается RthJC. Значение этой величины в основном зависит от типа корпуса и у современных транзисторов
составляет величину 0,4-1,5 (°С/Вт) или (К/Вт).
Q2 — значение теплового сопротивление корпус-радиатор стремиться к нулю в тех случаях, когда мы прикручиваем транзистор к
отполированной поверхности радиатора без изолирующих прокладок, или используем тонкие современные подложки из из оксида алюминия
(Al2O3), нитрида алюминия (AlN), или оксида бериллия (BeO). В случае применения слюды значение теплового сопротивления может составлять
0.2-1.5 (°С/Вт), в зависимости от толщины прокладки.
Т2 — максимальная температура кристалла транзистора, обозначается Tjmax и составляет для мощных транзисторов величину 120-175°С.
Т1 — максимально допустимая температура внутри корпуса, в котором находится радиатор, либо максимальная температура окружающей
среды, если рёбра радиатора выведены наружу.
ИТАК, РИСУЕМ ТАБЛИЧКУ ДЛЯ РАЧЁТА ПЛОЩАДИ РАДИАТОРА
— Максимальную температуру кристалла Т2 по возможности указываем на 20-30% ниже значения Tjmax, приведённого в
справочнике на полупроводник. Я бы рекомендовал подобрать это значение, исходя из температуры радиатора 60-70 градусов.
— Значение теплового сопротивления кристалл-корпус Q1 RthJC не гадая берём из справочника. Если совсем лень — ставим 1.
— Графу теплового сопротивления корпус-радиатор Q2 можно оставить без внимания, если транзистор сидит на радиаторе без всяких
прокладок, либо используются современные тонкие подложки, сдобренные специальными пастами. Если это не так, ищем в справочнике
параметр теплового сопротивления, на используемый вид подложки, и заносим его в таблицу.
— Так же оставляем в покое графу «скорость воздушного потока от вентилятора», если оный не предусмотрен нашей конструкцией.
А если предусмотрен, надо озадачиться выяснением этой самой величины скорости воздушного потока, омывающего наш теплоотвод.
Как? А приведу-ка я на следующей странице кусок главы из электротехнического справочника уважаемого автора Корякина-Черняка С. Л.,
посвящённый расчёту радиаторов, там кобыла и отыщется.
Как правило, значение этой величины находится в пределах 1-5 м/сек.
Если Вы вдруг озадачились рассеиванием на радиаторе слишком высоких мощностей, калькулятор может выдать отрицательные значения.
Смотрим формулу и видим — это нормально. Происходит это из-за ненулевого значения теплового сопротивления кристалл-корпус. Тут природу
не обманешь — надо либо поднимать значение максимальной температуры кристалла Т2, либо искать транзистор с меньшим тепловым
сопротивлением, либо сажать несколько транзисторов в параллель.
Теперь, что касается покупки радиатора по кропотливо рассчитанным нашей таблицей параметрам. Если производитель солидный, можно
воспользоваться приведённым в технической документации значением удельного теплового сопротивления. Параметр этот имеет размерность
дюйм*град/Вт, поэтому для пересчёта его в тепловое сопротивление всего радиатора, нам надо разделить это значение на длину в см.
и умножить на 2,54.
Если этот производитель Kinsten Industrial, или прочий китайский «no trademark» — воздержитесь от доверительных чувств
к указанному в DataSheet параметру теплового сопротивления, а лучше старательно, по приведённым чертежам, просчитайте суммарную
площадь подложки и граней, умножьте полученный результат на 2 и оценивайте возможность применения данной железяки в вашем
устройстве, исходя из общей площади поверхности радиатора.
С этим всё, дальше кусок из умного справочника.

РадиоКот :: Радиаторы и охлаждение.
РадиоКот >Статьи >
Радиаторы и охлаждение.
В физике, электротехнике и атомной термодинамике есть известный закон — ток, протекающий по проводам, нагревает их. Придумали его Джоуль и Ленц, и оказались правы — так оно и есть. Всё, что работает от электричества, так или иначе часть проходящей энергии передаёт в тепло.
Так уж получилось в электронике, что самым страдающим от тепла объектом нашей окружающей среды является воздух. Именно воздуху нагревающиеся детали передают тепло, а от воздуха требуется принять тепло и куда-нибудь подевать. Потерять, к примеру, или рассеять по себе. Процесс отдачи тепла мы с вами назовем охлаждением.
Наши электронные конструкции тоже рассеивают немало тепла, одни — больше, другие — меньше. Греются стабилизаторы напряжения, греются усилители, греется транзистор, управляющий релюшкой или даже просто мелким светодиодом, разве что греется ну совсем немного. Ладно, если греется немного. Ну а если он жарится так, что руку держать нельзя? Давайте пожалеем его и попробуем как-нибудь ему помочь. Так сказать, облегчить его страдания.
Вспомним устройство батареи отопления. Да, да, та самая обычная батарея, что греет комнату зимой и на которой мы сушим носки и футболки . Чем больше батарея, тем больше тепла будет в комнате, так ведь? По батарее протекает горячая вода, она нагревает батарею. У батареи есть важная вещь — количество секций. Секции контактируют с воздухом, передают ему тепло. Так вот, чем больше секций, то есть чем больше занимаемая площадь батареи, тем больше тепла она может нам отдать. Приварив еще парочку секций, мы сможем сделать теплее нашу комнату. Правда, при этом горячая вода в батарее может остыть, и соседям ничего не останется .
Рассмотрим устройство транзистора.
На медном основании (фланце) 1 на подложке 2 закреплен кристалл 3. Он подключается к выводам 4. Вся конструкция залита пластмассовым компаундом 5. У фланца есть отверстие 6 для установки на радиатор.
Вот это по сути та же самая батарея, посмотрите! Кристалл греется, это как горячая вода. Медный фланец контактирует с воздухом, это секции батареи. Площадь контакта фланца и воздуха — это место нагревания воздуха. Нагревающийся воздух охлаждает кристалл.
Как сделать кристалл холоднее? Устройство транзистора мы изменить не можем, это понятно. Создатели транзистора об этом тоже подумали и для нас, мучеников, оставили единственную дорожку к кристаллу — фланец. Фланец — это как одна-единственная секция у батареи — жарить жарит, а тепла воздуху не передается — маленькая площадь контакта. Вот тут предоставляется простор нашим действиям! Мы можем нарастить фланец, припаять к нему еще «парочку секций», то бишь большую медную пластинку, благо фланец сам медный, или же закрепить фланец на металлической болванке, называемой радиатором. Благо отверстие во фланце приготовлено под болт с гайкой.
Что же такое радиатор? Я твержу уже третий абзац про него, а толком так ничего и не рассказал! Ладно, смотрим:
Как видим, конструкция радиаторов может быть различной, это и пластинки, и ребра, а еще бывают игольчатые радиаторы и разные другие, достаточно зайти в магазин радиодеталей и пробежаться по полке с радиаторами . Радиаторы чаще всего делают из алюминия и его сплавов (силумин и другие). Медные радиаторы лучше, но дороже. Стальные и железные радиаторы применяются только на очень небольшой мощности, 1-5Вт, так как они медленно рассеивают тепло.
Тепло, выделяемое в кристалле, определяется по очень простой формуле P=U*I, где P — выделяемая в кристалле мощность, Вт, U = напряжение на кристалле, В, I — сила тока через кристалл, А. Это тепло проходит через подложку на фланец, где передается радиатору. Далее нагретый радиатор контактирует с воздухом и тепло передается ему, как следующему участнику нашей системы охлаждения.
Посмотрим на полную схему охлаждения транзистора.
У нас появились две штуки — это радиатор 8 и прокладка между радиатором и транзистором 7. Её может и не быть, что и плохо, и хорошо одновременно. Давайте разбираться.
Расскажу о двух важных параметрах — это тепловые сопротивления между кристаллом (или переходом, как его еще называют) и корпусом транзистора — Rпк и между корпусом транзистора и радиатором — Rкр. Первый параметр показывает, насколько хорошо тепло передается от кристалла к фланцу транзистора. Для примера, Rпк, равное 1,5градуса Цельсия на ватт, объясняет, что с увеличением мощности на 1Вт разница температур между фланцем и радиатором будет 1,5градуса. Иными словами, фланец всегда будет холоднее кристалла, а насколько — показывает этот параметр. Чем он меньше, тем лучше тепло передается фланцу. Если мы рассеиваем 10Вт мощности, то фланец будет холоднее кристалла на 1,5*10=15градусов, а если же 100Вт — то на все 150! А поскольку максимальная температура кристалла ограничена (не может же он жариться до белого каления!), фланец надо охлаждать. На эти же 150 градусов .
К примеру:
Транзистор рассеивает 25Вт мощности. Его Rпк равно 1,3градуса на ватт. Максимальная температура кристалла 140градусов. Значит, между фланцем и кристаллом будет разница в 1,3*25=32,5градуса. А поскольку кристалл недопустимо нагревать выше 140градусов, от нас требуется поддерживать температуру фланца не горячее, чем 140-32,5=107,5градусов. Вот так.
А параметр Rкр показывает то же самое, только потери получаются на той самой пресловутой прокладке 7. У нее значение Rкр может быть намного больше, чем Rпк, поэтому, если мы конструируем мощный агрегат, нежелательно ставить транзисторы на прокладки. Но всё же иногда приходится. Единственная причина использовать прокладку — если нужно изолировать радиатор от транзистора, ведь фланец электрически соединен со средним выводом корпуса транзистора.
Вот давайте рассмотрим еще один пример.
Транзистор жарится на 100Вт. Как обычно, температура кристалла — не более 150градусов. Rпк у него 1градус на ватт, да еще и на прокладке стоит, у которой Rкр 2градуса на ватт. Разница температур между кристаллом и радиатором будет 100*(1+2)=300градусов. Радиатор нужно держать не горячее, чем 150-300 = минус 150 градусов: Да, дорогие мои, это тот самый случай, который спасет только жидкий азот: ужос!
Намного легче живется на радиаторе транзисторам и микросхемам без прокладок. Если их нет, а фланцы чистенькие и гладкие, и радиатор сверкает блеском, да еще и положена теплопроводящая паста, то параметр Rкр настолько мал, что его просто не учитывают.
Разобрались? Поехали дальше!
Охлаждение бывает двух типов — конвекционное и принудительное. Конвекция, если помним школьную физику, это самостоятельное распространение тепла. Так же и конвекционное охлаждение — мы установили радиатор, а он сам там как-нибудь с воздухом разберется. Радиаторы конвекционного типа устанавливаются чаще всего снаружи приборов, как в усилителях, видели? По бокам две металлические пластинчатые штуковины. Изнутри к ним привинчиваются транзисторы. Такие радиаторы нельзя накрывать, закрывать доступ воздуха, иначе радиатору некуда будет девать тепло, он перегреется сам и откажется принимать тепло у транзистора, который долго думать не будет, перегреется тоже и: сами понимаете что будет. Принудительное охлаждение — это когда мы заставляем воздух активнее обдувать радиатор, пробираться по его ребрам, иглам и отверстиям. Тут мы используем вентиляторы, различные каналы воздушного охлаждения и другие способы. Да, кстати, вместо воздуха запросто может быть и вода, и масло, и даже жидкий азот . Мощные генераторные радиолампы частенько охлаждаются проточной водой.
Как распознать радиатор — для конвекционного он или принудительного охлаждения? От этого зависит его эффективность, то есть насколько быстро он сможет остудить горячий кристалл, какой поток тепловой мощности он сможет через себя пропустить.
Смотрим фотографии.
Первый радиатор — для конвекционного охлаждения. Большое расстояние между ребрами обеспечивает свободный поток воздуха и хорошую теплоотдачу. На второй радиатор сверху одевается вентилятор и продувает воздух сквозь ребра. Это принудительное охлаждение. Разумеется, использовать везде можно и те, и те радиаторы, но весь вопрос — в их эффективности.
У радиаторов есть 2 параметра — это его площадь (в квадратных сантиметрах) и коэффициент теплового сопротивления радиатор-среда Rрс (в Ваттах на градус Цельсия). Площадь считается как сумма площадей всех его элементов: площадь основания с обеих сторон + площадь пластин с обеих сторон. Площадь торцов основания не учитывается, так там квадратных сантиметров ну совсем немного будет .
Пример:
радиатор из примера выше для конвекционного охлаждения.
Размеры основания: 70х80мм
Размер ребра: 30х80мм
Кол-во ребер: 8
Площадь основания: 2х7х8=112кв.см
Площадь ребра: 2х3х8=48кв.см.
Общая площадь: 112+8х48=496кв.см.
Коэффициент теплового сопротивления радиатор-среда Rрс показывает, на сколько увеличится температура выходящего с радиатора воздуха при увеличении мощности на 1Вт. Для примера, Rрс, равное 0,5 градуса Цельсия на Ватт, говорит нам, что температура увеличится на полградуса при нагреве на 1Вт. Этот параметр считается трехэтажными формулами и нашим кошачьим умам ну никак не под силу: Rрс, как и любое тепловое сопротивление в нашей системе, чем меньше, тем лучше. А уменьшить его можно по-разному — для этого радиаторы чернят химическим путем (например алюминий хорошо затемняется в хлорном железе — не экспериментируйте дома, выделяется хлор!), еще есть эффект ориентировать радиатор в воздухе для лучшего прохождения его вдоль пластин (вертикальный радиатор лучше охлаждается, чем лежачий). Не рекомендуется красить радиатор краской: краска — лишнее тепловое сопротивление. Если только слегка, чтобы темненько было, но не толстым слоем!
В приложении есть маленький программчик, в котором можно посчитать примерную площадь радиатора для какой-нибудь микросхемы или транзистора. С помощью него давайте рассчитаем радиатор для какого-нибудь блока питания.
Схема блока питания.
Блок питания выдает на выходе 12Вольт при токе 1А. Такой же ток протекает через транзистор. На входе транзистора 18Вольт, на выходе 12Вольт, значит, на нем падает напряжение 18-12=6Вольт. С кристалла транзистора рассеивается мощность 6В*1А=6Вт. Максимальная температура кристалла у 2SC2335 150градусов. Давайте не будем эксплуатировать его на предельных режимах, выберем температуру поменьше, для примера, 120градусов. Тепловое сопротивление переход-корпус Rпк у этого транзистора 1,5градуса Цельсия на ватт.
Поскольку фланец транзистора соединен с коллектором, давайте обеспечим электрическую изоляцию радиатора. Для этого между транзистором и радиатором положим изолирующую прокладку из теплопроводящей резины. Тепловое сопротивление прокладки 2градуса Цельсия на ватт.
Для хорошего теплового контакта капнем немного силиконового масла ПМС-200. Это густое масло с максимальной температурой +180градусов, оно заполнит воздушные промежутки, которые обязательно образуются из-за неровности фланца и радиатора и улучшит передачу тепла. Многие используют пасту КПТ-8, но и многие считают её не самым лучшим проводником тепла.
Радиатор выведем на заднюю стенку блока питания, где он будет охлаждаться комнатным воздухом +25градусов.
Все эти значения подставим в программку и посчитаем площадь радиатора. Полученная площадь 113кв.см — это площадь радиатора, рассчитанная на длительную работу блока питания в режиме полной мощности — дольше 10часов. Если нам не нужно столько времени гонять блок питания, можно обойтись радиатором поменьше, но помассивнее. А если мы установим радиатор внутри блока питания, то отпадает необходимость в изолирующей прокладке, без нее радиатор можно уменьшить до 100кв.см.
А вообще, дорогие мои, запас карман не тянет, все согласны? Давайте думать о запасе, чтобы он был и в площади радиатора, и в предельных температурах транзисторов. Ведь ремонтировать аппараты и менять пережаренные транзисторы придется не кому-нибудь, а вам самим! Помните об этом!
Удачи.
Вопросы складываем сюда.
Как вам эта статья? | Заработало ли это устройство у вас? |
⚡️Как рассчитать радиатор для КРЕНки
На чтение 5 мин. Опубликовано
Обновлено
Во время своей работы интегральные стабилизаторы напряжения, особенно линейные, выделяют в окружающую среду определенное количество тепла. Если заранее не позаботиться об их охлаждении, то они могут выйти из строя, из-за перегрева рабочей структуры кристалла.
Для обеспечения высокой точности и стабильности напряжения питания в современных электронных устройствах широкое распространение получили интегральные стабилизаторы напряжения (ИМС) серии хх78хх (отечественный аналог КР142) которые производят многие зарубежные фирмы. Параметры некоторых ИМС стабилизаторов напряжения согласно данным из [1], приведены в табл.1.

При мощности нагрузки более 1 Вт, ИМС линейного стабилизатора напряжения необходимо эксплуатировать с теплоотводом, к которому они крепятся болтовым соединением. Промышленность выпускает различные виды радиаторов на любой вкус: пластинчатые, ребристые, штыревые, игольчатые и др. Выбор теплоотвода сводится к определению его конструкции и размеров, которые обеспечат теплостойкость.
Охладитель в форме пластины конечно очень прост в изготовлении, имеет сравнительно небольшую стоимость. Площадь его поверхности равна сумме площадей двух сторон. Для изготовления пластинчатых охладителей следует использовать алюминиевые пластины с толщиной 1.5…3 мм. Такие радиаторы целесообразно применять при небольших мощностях рассеивания, т.к. иначе такой радиатор получается очень габаритным.
Для повышения эффективности теплоотвода и уменьшения габаритов целесообразно использовать ребристые и штыревые охладители. Ребристый радиатор обычно бывает или цельнолитой, либо фрезерованный, а также может быть с одно или двухсторонним оребрением. Двухстороннее оребрение позволяет увеличить площадь поверхности. Самым эффективным является штыревой (игольчатый) теплоотвод, который не требует строгой пространственной ориентации в электронном устройстве.
При минимальном объеме такой радиатор имеет эффективную максимальную площадь рассеивания. Площадь поверхности у такого радиатора равна сумме площадей каждого штырька плюс площадь основания. Материалом для радиаторов обычно служит алюминий и его сплавы. Лучшей эффективностью отвода тепла обладают охладители, выполненные из меди, однако вес и стоимость у таких радиаторов больше, чем у алюминиевых теплоотводов.
Пример расчета
Расчет будем производить на примере стабилизатора напряжения LM7805 (аналог КР142ЕН5В). Для расчета нужны следующие данные:
- Максимальное напряжение питания, подаваемое на стабилизатор Umax = 15В; напряжение на выходе стабилизатора Uвыx= 5В;
- Максимальный ток нагрузки Iн = 1А;
- Допустимую температуру радиатора примем равной Т = 50°C.
Максимальное падение напряжения ΔU на стабилизаторе напряжения определяется согласно формуле (1):
ΔU = Umax — Uвых = 15 — 5 = 10В (1)
Тогда мощность, рассеиваемая на стабилизаторе, составит:
Ррас = ΔU*Iн= 10*1 = 10 Вт; (2)
Из справочных данных известно, что стабилизаторы серии КР142 могут рассеивать мощность без теплоотвода до 1 Вт. В нашем же случае это условие не выполняется, так как Ррас = 10 Вт, это означает, что нужно проводить расчет далее. Существует такой параметр как тепловое сопротивление Q, к сожалению, в справочной литературе приводиться крайне редко.
Показывает он на сколько °С нагревается радиоэлемент, если в нем выделяется мощность в 1 Вт. Однако, его можно определить двумя способами: или по формуле, или исходя из типа корпуса интегрального стабилизатора напряжения. Т. к. ИМС серии КР142 выпускаются в корпусе ТО220, то из [2] следует, что тепловое сопротивление этого стабилизатора напряжения будет 2…5 °С / Вт.
Мы можем рассчитать тепловое сопротивление Q, помня, что Т = 50°С
Q = T / Pрас = 50 / 10 = 5°С / Вт (3)
Полученный результат совпадает с цифрами, приведенными в [2].
Площадь радиатора S определяется согласно формуле:
S = (T/Q)² = (50 /5)²= 100 см² (4)
Из приведенного расчета можно сделать небольшой вывод, что на 1 Вт рассеиваемой мощности стабилизатора напряжения необходим радиатор площадью 10 см². Чтобы теплоотвод занял как можно меньше места на плате проектируемого устройства, целесообразно применить ребристый охладитель, эскиз которого показан на рисунке.

Определение площади ребристого радиатор
Определим площадь теплоотвода на примере все того же ребристого радиатора, но не на основании предельно допустимых параметров работы интегрального стабилизатора напряжения, а на основании габаритных размеров теплоотвода.
На рисунке условно показаны размеры необходимые для данного расчета. Из [2] воспользуемся формулами для расчета площади радиатора:
S = [2*(H-d) + D] * (n-1) * L+ L* [В + 2 * Н + (d* n)] (5)
S = 2 * L (B = H) + 2 * В * Н (6)
где n количество ребер радиатора.
Производить расчет ребристого радиатора можно по одной из двух формул (5) или (6). При расчете по формуле (6) задаемся условием, что в процессе охлаждения участвует в основном наружная поверхность теплоотвода так называемый теплообмен излучением, и зависит в основном от коэффициента излучения (степени черноты) материала радиатора. При расчете по формуле (5) в процессе охлаждения участвует как наружная, так и внутренняя поверхность (межреберное пространство) это так называемый конвективный способ передачи тепла.
Однако не стоит забывать о том, что не все ребра охладителя могут одинаково отводить выделяемое тепло, так как часть их поверхности, может соприкасаться с другими деталями и узлами находящиеся на плате. Этот факт следует также учитывать, при разработке какого-либо электронного устройства с применением стабилизатора напряжения.
Хотелось бы также отметить, что при естественном воздушном теплоотводе примерно 70% тепла отводиться конвекцией, а 30% приходиться на излучение. Следует также помнить, что при монтаже стабилизатора напряжения, теплоотвод установленный на нем будет иметь электрическую связь со средним выводом микросхемы серии хх78хх (КР142).
Расчёт радиаторов для транзисторов и микросхем. Онлайн калькулятор теплоотводов.
На предыдущей странице ссылка на страницу был приведён калькулятор для расчёта площадей
радиаторов для транзисторов, микросхем и прочих полупроводников. Большая часть необходимой информации была почерпнута
из методики, основанной на рекомендациях по выбору алюминиевых радиаторов фирмы Aavid Thermalloy, являющейся
бесспорным лидером в производстве стандартных радиаторов для воздушного и жидкостного охлаждения.
А познакомиться с этой информацией можно благодаря электротехническому справочнику уважаемого автора, главу из которого я и приведу на
этой странице. Для специалистов, проектирующих силовую электронику — «очень своевременная книга» (В. И. Ленин).
ЭЛЕКТРОТЕХНИЧЕСКИЙ СПРАВОЧНИК
Автор: Корякин-Черняк С.Л.
18.4.4. Как рассчитать радиатор?
Во время работы полупроводникового прибора в его кристалле выделяется мощность, которая приводит к разогреву последнего.
Если тепла выделяется больше, чем рассеивается в окружающем пространстве, то температура кристалла будет расти и может превысить
максимально допустимую. При этом его структура будет необратимо разрушена.
Следовательно, надежность работы полупроводниковых приборов во многом определяется эффективностью их охлаждения.
Наиболее эффективным является конвективный механизм охлаждения, при котором тепло уносит поток газообразного или жидкого
теплоносителя, омывающего охлаждаемую поверхность.
Чем больше охлаждаемая поверхность, тем эффективнее охлаждение, и поэтому мощные полупроводниковые приборы нужно устанавливать на
металлические радиаторы, имеющие развитую охлаждаемую поверхность. В качестве теплоносителя обычно используется окружающий воздух.
По способу перемещения теплоносителя различают:
— естественную вентиляцию;
— принудительную вентиляцию.
В случае естественной вентиляции перемещение теплоносителя осуществляется за счет тяги, возникающей возле нагретого радиатора.
В случае принудительной вентиляции перемещение теплоносителя осуществляется с помощью вентилятора. Во втором случае можно получить
большие скорости потока и, соответственно, лучшие условия охлаждения.
Тепловые расчеты можно сильно упростить, если использовать тепловую модель охлаждения (рис. 18.26) Здесь разница между температурой
кристалла TJ и температурой среды ТA вызывает тепловой поток, движущийся от кристалла к окружающей среде,
через тепловые сопротивления RJC (кристалл — корпус), RCS (корпус — радиатор) и RSA
(радиатор — окружающая среда). 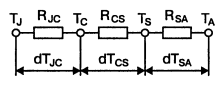
Рис 18.26. Тепловая модель охлаждения
Тепловое сопротивление имеет размерность °С/Вт. Суммарное максимальное тепловое сопротивление RJA на участке кристалл —
окружающая среда можно найти по формуле: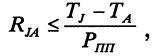
где РПП — мощность, рассеиваемая на кристалле полупроводникового прибора, Вт.
Тепловое сопротивление RJC и RCS указывается в справочных данных на полупроводниковые приборы.
Например, согласно справочным данным, на транзистор IRFP250N, его тепловое сопротивление на участке кристалл- радиатор
равно RJC + RCS = 0,7 + 0,24 = 0,94 °С/ Вт.
Это означает, что если на кристалле выделяется мощность 10 Вт, то его температура будет на 9,4 °С больше температуры радиатора.
Тепловое сопротивление радиатора можно найти по формуле: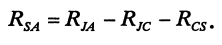
Предлагаемая ниже методика основана на рекомендациях по выбору алюминиевых радиаторов серии Max Clip System™ фирмы
«AAVID THERMALLOY».
На рис. 18.27 приводятся графические зависимости между периметром сечения алюминиевого радиатора и его тепловым сопротивлением
для естественного (красная линия) и принудительного (синяя линия) охлаждения воздушным потоком.
По умолчанию считается, что:
— радиатор имеет длину 150 мм;
— разница между температурой радиатора TS и температурой окружающей среды Та равна 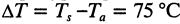
— скорость потока принудительного охлаждения равна 2 м/с.
Если условия охлаждения отличаются от принятых по умолчанию, то необходимую поправку можно внести, воспользовавшись
графиками на рис. 18.28 — рис. 18.30. 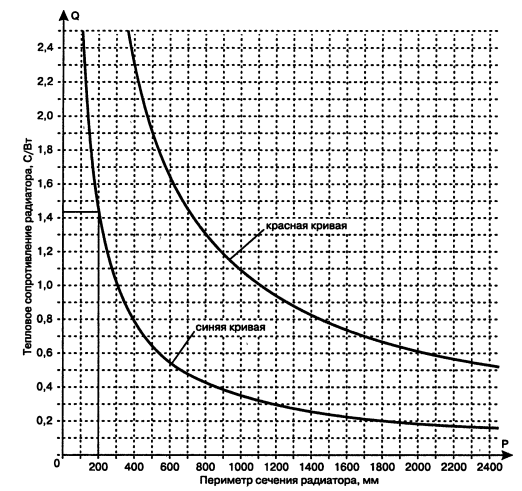
Рис. 18.27. Зависимости между сечением алюминиевого радиатора и его тепловым сопротивлением
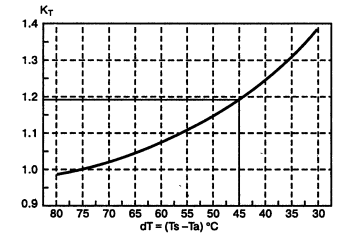
Рис. 18.28. Поправочный коэффициент на разницу температуры радиатора и окружающей среды
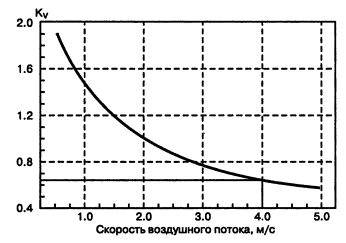
Рис. 18.29. Поправочный коэффициент на скорость воздушного потока
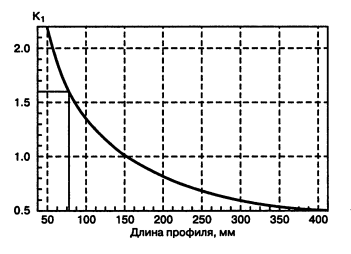
Рис. 18.30. Поправочный коэффициент на длину радиатора
Для примера рассчитаем радиатор, обеспечивающий охлаждение транзистора ЭРСТ, состоящего из 20-ти транзисторов типа IRFP250N.
Расчет радиатора можно вести для одного транзистора, а затем полученный размер увеличить в 20 раз.
Так как на ключевом транзисторе рассеивается суммарная мощность 528 Вт, то на каждом транзисторе IRFP250N рассеивается мощность
528/20 = 26,4 Вт. Радиатор должен обеспечивать максимальную температуру кристалла транзистора не более +110 °С при максимальной
температуре окружающей среды +40 °С.
Найдем тепловое сопротивление RJA для одного транзистора IRFP250N: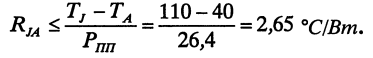
Теперь найдем тепловое сопротивление радиатора: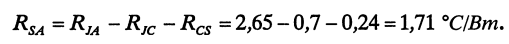
Зная максимальную температуру кристалла и тепловое сопротивление на участке кристалл-радиатор, определим максимальную
температуру радиатора: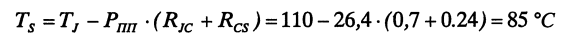
По графику (рис. 18.28) определим поправочный коэффициент Кт на разницу температуры радиатора и окружающей среды: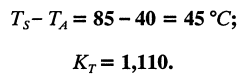
Для охлаждения радиатора используется вентилятор типа 1,25ЭВ-2,8-6-3270У4, имеющий производительность 280 м3/ч.
Чтобы вычислить скорость потока, нужно разделить производительность на сечение воздуховода, продуваемого вентилятором.
Если воздуховод имеет площадь поперечного сечения: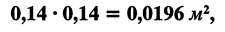
то скорость воздушного потока будет равна: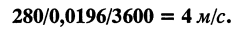
По графику (рис. 18.29) определим поправочный коэффициент Kv на реальную скорость воздушного потока: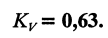
Допустим, что в нашем распоряжении имеется большое количество готовых радиаторов, имеющих периметр сечения 1050 мм и длину 80 мм.
По графику (рис. 18.30) определим поправочный коэффициент KL на длину радиатора: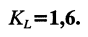
Чтобы найти общую поправку, перемножим все поправочные коэффициенты: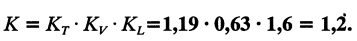
С учетом поправок, радиатор должен обеспечивать тепловое сопротивление: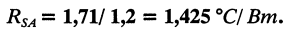
С помощью графика (рис. 18.27) найдем, что для одного транзистора требуется радиатор с периметром сечения 200 мм.
Для группы из 20-ти транзисторов IRFP250N радиатор должен иметь периметр сечения не менее 4000 мм. Так как имеющиеся в
распоряжении радиаторы имеют периметр 1050 мм, то придется объединить 4 радиатора.
На диоде ЭРСТ рассеивается меньшая мощность, но из конструктивных соображений для него можно использовать аналогичный радиатор.
Зачастую производители охладителей указывают площадь поверхности радиатора, а не периметр и длину.
Чтобы из предлагаемой методики получить площадь радиатора, достаточно умножить длину радиатора на его периметр SP = 400 • 8 = 3200 см2.

Точный расчет количества радиаторов (секций) отопления
Можно провести расчет радиаторов отопления по площади, с помощью калькулятора, размещенного на каком-либо сайте. Но данные не будут точными. Калькуляторов (программ) расчета секций радиаторов отопления много, но точную информацию можно получить только в том случае, если провести расчет вручную индивидуально для каждого помещения.
Упрощенные варианты расчета радиаторов отопления в доме
Первый способ: Расчет по объему комнат
Он прописан в положениях СНиП и применим для панельных домов, Правила предлагают в качестве нормы взять 41 Вт мощности отопления на один кубический метр отапливаемого помещения. Чтобы рассчитать количество необходимых секций достаточно объем комнаты разделить на мощность одной секции устанавливаемых радиаторов (этот параметр указывается производителем в сопроводительной технической документации).
Второй способ: Расчет по площади помещений
Данный способ расчета ориентирован на помещения с потолками до 2500 мм, и за норму берется 100 Вт мощности на один квадрат площади. Для расчёта количества секций необходимо разделить площадь помещения на мощность одной секции (указывается в технической документации радиаторов).
Примерный расчет количества секций радиатора для типового помещения
N=S/P*100, где:
- N — Количество секций (дробная часть округляется по правилам математического округления))
- S — Площадь комнаты в м2
- P — Теплоотдача 1 секции, Ватт
Для этих вариантов расчета применим ряд поправок. Например, если в помещении имеется балкон, или более двух окон, или оно находится на углу здания, то к полученному количеству секций рекомендуется приплюсовать еще 20%. Если при расчете получается конечный результат (количество секций) дробное число, то его следует округлять до целого в большую сторону.
Обратите внимание: полученное значение рассчитано для идеальных условий. То есть, в доме нет дополнительных теплопотерь, сама система отопления работает эффективно, окна и двери герметично закрываются, а соседние помещения также отапливаются. В реальных условиях секций может потребоваться больше.
Точный расчет необходимого количества секций радиаторов
Выше приведены упрощенные способы расчета радиаторов, которые актуальны для типовых квартир со стандартными параметрами. С их помощью получить адекватный результат для частных жилых домов и квартир в современных новостройках нереально. Для этого следует использовать специальную формулу:
КТ = 100Вт/м2 * S * К1 * К2 * К3 * К4 * К5 * К6 * К7,
Где за основу также берется норма в 100 Вт на квадратный метр, общая площадь помещения и дополняется коэффициентами, значения которых приведены ниже:
K1 — коэффициент, учитывающий остекление оконных проемов:
- для окон с обычным двойным остеклением: 1.27;
- для окон с двойным стеклопакетом: 1.0;
- для окон с тройным стеклопакетом: 0.85;
K2 — коэффициент теплоизоляции стен:
- низкая степень теплоизоляции: 1.27;
- хорошая теплоизоляция (кладка в два крипича или слой утеплителя): 1.0;
- высокая степень теплоизоляции: 0.85;
K3 — соотношение площади окон и пола в помещении:
- 50%: 1.2;
- 40%: 1.1;
- 30%: 1.0;
- 20%: 0.9;
- 10%: 0.8;
K4 — коэффициент, позволяющий учесть среднюю температуру воздуха в самую холодную неделю года:
- для -35°C: 1.5;
- для -25°C: 1.3;
- для -20°C: 1.1;
- для -15°C: 0.9;
- для -10°C: 0.7;
K5 — корректирует потребность в тепле с учетом количества наружных стен:
- одна стена: 1.1;
- две стены: 1.2;
- три стены: 1.3;
- четыре стены: 1.4;
K6 — учет типа помещения, которое расположено выше:
- холодный чердак: 1.0;
- отапливаемый чердак: 1.0;
- отапливаемое жилое помещение: 1.0;
K7 — коэффициент, учитывающий высоту потолков:
- при 2.5 м: 1.0;
- при 3.0 м: 1.05;
- при 3.5 м: 1.1;
- при 4.0 м: 1.15;
- при 4.5 м: 1.2;
По этой формуле вы сможете рассчитать общее количества тепла, необходимого для того или иного помещения. Для определения количества секций радиаторов, вам необходимо полученный результат разделить на мощность одной секции.
Как рассчитать количество радиаторов отопления в доме

Добиться от системы отопления полной эффективности и экономичности — нормальное желание хозяина дома. Как рассчитать количество радиаторов отопления в доме? Существует ли универсальная формула, позволяющая получить точный ответ и сразу заказать определенное количество приборов?
Да, формулы существуют, они разработаны с учетом действующих СНиП, но применить их конкретному частному дому без специальных знаний довольно сложно. Это стоит объяснить отдельно. Для расчета потребности в тепловой энергии применяется сложная система коэффициентов, в которой учитывается все, что может повлиять на обогрев — от площади комнаты до этажа и определенного типа радиаторов. Таким образом можно получить довольно точные значения, но в реальности это необходимо в случаях, когда речь идет о большом строительном проекте, поскольку общее количество приборов и выделяемое ими тепло с учетом потерь составляют внушительные суммы в денежном эквиваленте.
Способы и методики расчета количества радиаторов
Для частного дома, пусть и большого, такая точность не нужна, но узнать, сколько потребуется установить радиаторов, все же необходимо. Поэтому мы рассмотрим ответы в виде самых простых примеров:
- расчет количества радиаторов в системе отопления частного дома по объему помещений;
- расчет с учетом площади помещений;
- расчет с использованием простого калькулятора;
- описание некоторых поправочных коэффициентов, применяемых в профессиональном проектировании.
Любой из этих вариантов даст приемлемый по точности результат, а если вы все же хотите получить точные данные, то лучше поручить эту задачу профессионалу в области проектирования.
Какой тип радиаторов нам интересен
Для примера возьмем трубчатые стальные радиаторы КЗТО из серии Гармония — их параметры можно уверенно считать наиболее подходящими для подбора в частный дом. Варианты с чугунными, алюминиевыми, биметаллическими и панельными радиаторами демонстрируют крайности либо в цене, либо в эффективности теплоотдачи.
При изучении продукции в таблице с характеристиками радиаторов можно найти их мощность, количество секций и размеры. Поэтому мы не будем делать конкретный расчет, а приведем пример в виде описания порядка действий.
Расчет по объему помещения
Самый простой и доступный вариант расчетов количества радиаторов для частного дома учитывает объем помещения. При отступлении от стандартной высоты потолков в 2,7 м это дает возможность опираться на реальные размеры. Сначала узнаем объем помещения в метрах кубических — умножаем площадь на высоту. Для того, чтобы узнать потребность в тепловой энергии, можно применить средний вариант — 41 ватт на кубометр дает комфортную температуру примерно в 20 С даже в панельных многоэтажках. Умножаем 41 на объем помещения, подбираем радиатор по таблице, в которой указаны размеры, количество секций и тепловая мощность, делим цифру потребности на мощность одного прибора и получаем их количество для одного помещения.
Расчет по площади помещения
Теперь посмотрим, как рассчитать радиаторы отопления по площади. Здесь можно условно принять высоту потолков за 2,7 м , а потом ввести поправку, если помещение выше. Исходим из следующих условий:
- дом расположен в средней полосе России;
- используются трубчатые стальные радиаторы;
- площадь помещения известна;
- стены кирпичные, в два кирпича, с хорошей теплоизоляцией.
Для обогрева помещения в таких условиях достаточно затратить от 60 до 100 Ватт на квадратный метр. Принцип расчета тот же — находим в таблице радиатор КЗТО с подходящими нам размерами, узнаем там же его тепловую мощность, делим потребность на мощность прибора.
Может ли возникнуть ситуация, при которой в доме все равно будет прохладно? Может, например в зоне, где часто и подолгу держатся морозы. Тогда потребуется исходить из потребности 150 — 200 Ватт на квадратный метр. Но это еще не все — есть ряд факторов, которые влияют на теплопотери дома. Например, радиатор отопления для дачи, может работать в режиме с пониженной теплоотдачей из-за маломощного котла, а само строение окажется недостаточно утепленным.
Поправочные коэффициенты для точного расчета
Для того, чтобы учесть эти особенности, вводится еще ряд поправочных коэффициентов, на которые умножают полученное значение потребности в тепловой энергии. Во внимание принимается:
- площадь и количество окон;
- соотношение площади стен и остекления;
- наличие и утепление чердака;
- качество стен, характер теплоизоляции;
- расположение радиаторов в помещении;
- тепловой напор — разница между температурой в помещении и температурой радиаторов;
- тип системы отопления — двухтрубная или однотрубная.
Если вы решите, что необходимо учесть все особенности дома, то расчетом должен заниматься только специалист. Пример поправочных коэффициентов при расчете потребности в радиаторах отопления в одном помещении в зависимости от площади остекления и пола:
- 10% — 0,8
- 20% — 0,9
- 30% — 1,0
- 40% — 1,1
- 50% — 1,2
Пример расчета в зависимости от наличия теплоизоляции, если считать нормой стену в два кирпича:
- кирпичные стены — 1,0
- недостаточная (отсутствует) — 1,27
- хорошая — 0,8
Пример расчета в зависимости от того, сколько стен в помещении выходит наружу:
- внутреннее помещение — 1,0
- одна — 1,1
- две — 1,2
- три — 1,3
На профессиональном уровне учитывается очень много параметров, поэтому произвести такой расчет самостоятельно вам не удастся. Обратитесь к специалистам компании КЗТО, мы с удовольствием выполним этот расчет для Вас и подберем оптимальное количество и модели радиаторов отопления, учитывая все ваши пожелания.
Расчет количества радиаторов отопления по площади помещения |Системы отопления
КОНСТРУКТИВНЫЕ ОСОБЕННОСТИ ПАНЕЛЬНЫХ РАДИАТОРОВ ОТОПЛЕНИЯ
Основным материалом для изготовления панельных радиаторов является сталь. Сталь, как высокотехнологичный материал обладает отличным набором свойств: прочность, ковкость, гибкость – всё это предает агрегатам из стали массу полезных свойств, а хорошая податливость сварке и высокая теплопроводность делают сталь идеальным материалом для радиаторов отопления.
Главной конструктивной единицей панельного радиатора является панель, которых, в зависимости от типа радиатора, может быть и одна, и две, и три.
Панель радиатора – это два сваренных между собой тонких стальных листа. Листы же до сварки проходят штамповку, где им предаётся профиль – это и есть каналы для циркуляции нагретой жидкости в панели радиатора. Панели, если их две и более, соединенные между собой трубками, с металлическим кожухом по бокам и декоративной верхней решеткой и есть готовый панельный радиатор отопления.
Для повышения теплоотдачи и скорости обогрева помещения, радиатор может оснащаться конвекционными ходами с внутренней стороны панелей в виде ребристого листа из более тонкой стали, что способствует перемещению воздушных масс в помещении и равномерному обогреву.
Как видно, технология изготовления данных агрегатов проста, что и объясняет их достаточно низкую стоимость.
Если производитель не экономит на качестве материала и для производства радиаторов использует качественную сталь, применяет современные технологичные методы нанесения защитного покрытия, то такой радиатор гарантированно и бесперебойно служит долгие годы.
В зависимости от количества панелей и конвекторов панельные радиаторы делятся на типы. Двухзначное число к маркировке панельного радиатора является обозначением его принадлежности к определенному типу, где первая цифра – это количество панелей, а вторая, соответственно, количество конвекторов.
ТИПЫ ПАНЕЛЬНЫХ РАДИАТОРОВ ОТОПЛЕНИЯ
Тип 10 – панельный радиатор, состоящий из одной панели без конвектора, кожухов и верхней решетки.
Тип 20 – панельный радиатор, состоящий из соединенных между собой патрубками двух панелей, без конвектора, кожухов и закрытый верхней решетки.
Тип 30 – панельный радиатор, состоящий из соединенных между собой патрубками трех панелей, без конвектора, кожухов и закрытый верхней решетки.
Тип 11 – панельный радиатор, состоящий из одной панели, одного конвектора, без кожухов и верхней решетки.
Тип 21 – панельный радиатор, состоящий из соединенных между собой патрубками двух панелей, одним конвектором, закрытый кожухом и верхней решеткой.
Тип 22 – панельный радиатор, состоящий из соединенных между собой патрубками двух панелей, двумя конвекторами, закрытый кожухом и верхней решеткой.
Тип 33 – панельный радиатор, состоящий из соединенных между собой патрубками трех панелей, тремя конвекторами, закрытый кожухом и верхней решеткой.
ПОДБОР ТРЕБУЕМОГО ПАНЕЛЬНОГО РАДИАТОРА, РАСЧЕТ ПО ПЛОЩАДИ ПОМЕЩЕНИЯ
Панельный радиатор является эффективным отопительным агрегатом и за счет большой нагреваемой площади имеет повышенную теплоотдачу. Панельные радиаторы имеют широкий диапазон размеров, как по вертикали, от 300 до 900 мм, так и по горизонтали, от 400 до 3000 мм.
В зависимости от размера и типа панельного радиатора меняется и его показатель теплоотдачи, то есть количество отдаваемого тепла радиатором в единицу времени, который измеряется в Ваттах (Вт). Каждый радиатор, помимо маркировки типа и габаритов имеет свой основной показатель – тепловую мощность.
Есть усредненные простейшие формулы расчета требуемой суммарной тепловой мощности для отопления помещений.
Первый способ, исходит из расчета в 100 Вт на 1 м² помещения. Для примера, если комната 15 м² то 100 х 15 = 1 500 Вт. Соответственно, нам необходим радиатор мощностью не ниже 1 500 Вт, к примеру подойдет панельный радиатор 500х800, тип 22 с мощностью 1 515 Вт.
Но существует множество внешних факторов и переменных, влияющих на сумму необходимой тепловой энергии для поддержания комфортной температуры в комнате.
Факторы влияния есть очевидные: высота потолков, количество окон, наличие наружной двери в комнате, теплоизоляция дома – пола, стен и потолков, метод подключения и расположение радиаторов отопления. Но не менее важными факторами будут и роза ветров, верхний и нижний температурные пороги в отапливаемое время года, даже ориентация стен по сторонам света.
В действительности сложно учесть все эти факторы для точного расчета требуемой тепловой мощности и для бытового расчета приняты некоторые правила:
— наличие окна в помещении + 100 Вт;
— наличие наружной двери + 200;
— суммарное влияние всех неучтенных факторов + 20% к полученной сумме требуемой тепловой мощности.
Во второй формуле будем исходить из расчета в 40 Вт на 1 м³ и учета вышеизложенных правил.
К примеру, комната 3 на 6 метров и высотой потолков 3,2 метров, двумя окнами, одно шириной 900 мм, второе — 1200 мм и внешней дверью:
(3 х 6 х 3,2 х 40 + (100 х 2) + 200) + 20% = 3 245 Вт
Итого, 3 245 Вт тепловой энергии радиаторов требуется для обогрева нашей комнаты.
3 245 / 2 окна и получаем среднюю тепловую мощность на один радиатор, равную 1 622 Вт
Конечно, можно установить под каждое окно в комнате по одному радиатору Airfel 500×900, тип 22 с тепловой мощностью 1704, но для достижения максимального эффекта необходимо учесть и размеры оконных проёмов.
Касаемо установки самих радиаторов, необходимо следовать некоторым правилам. Например, при наличии окон в комнате, как во втором примете, радиаторы нужно устанавливать на стене под окнами, чтобы конвекционный поток нагретого воздуха создавал тепловой щит. Также радиатор должен быть равен минимум 80% от ширины оконного проема.
А теперь, воспользовавшись таблицей отдаваемой тепловой мощности и учитывая количество окон в комнате и их ширину проемов, подберем панельный радиатор, отвечающий нашим требованиям:
ТАБЛИЦА ТЕПЛООТДАЧИ ПАНЕЛЬНЫХ РАДИАТОРОВ AIRFEL
Изучив таблицу теплоотдачи, рекомендовано в комнате из примера установить два отопительных радиатора, один — Airfel 500×800 mm с тепловой мощностью 1515 Вт под окном шириной 900 мм и второй — Airfel 500×1000 mm с тепловой мощностью 1894 Вт под окном шириной 1200 мм. Мощности подобранных радиаторов будет достаточно для отопления нашей комнаты, а оставшийся запас можно использовать во время резкого похолодания, тем самым избежать перепадов температуры в помещении.
ТАБЛИЦА ТЕПЛООТДАЧИ ПАНЕЛЬНЫХ РАДИАТОРОВ PRADO
Радиаторы тепла — Atomic Rockets
Расчетные факторы
Используя уравнение Стефана Больцмана, мы можем быстро увидеть, что радиатор с лучшим коэффициентом излучения, большей площадью поверхности и более высокой температурой удаляет больше отработанного тепла.
На космических кораблях важно использовать самые легкие компоненты для каждой задачи. Космический корабль с более легкими радиаторами будет быстрее ускоряться и иметь больше deltaV, что означает, что он может идти дальше и делать больше при меньшем количестве топлива.
Если нам нужен легкий радиатор, мы хотим, чтобы он имел самый высокий коэффициент излучения. Мы можем добиться этого, используя естественно темные материалы, такие как графит, или закрашивая блестящие металлы черной краской.
Радиатор большего размера весит больше. Поэтому нам нужны радиаторы минимального размера. Чтобы компенсировать меньшую площадь поверхности, мы можем увеличить рабочую температуру. Небольшое повышение температуры приводит к значительному увеличению удаляемого отходящего тепла. Это означает, что горячие радиаторы намного легче и меньше холодных.
Дополнительные сведения
- Система EAC МКС
Типичный радиатор принимает охлаждающую жидкость от горячего компонента. Температура компонента охлаждающей жидкости на выходе — это начальная температура в радиаторе. Радиатор служит интерфейсом, который отводит тепло охлаждающей жидкости, что приводит к более низкой температуре на выходе из радиатора. Охлаждающая жидкость возвращается к компоненту для завершения цикла отвода отходящего тепла.
- Обратите внимание на то, что максимальная температура теплообменника, передаваемая пару, является самой низкой температурой жидкого натрия в активной зоне реактора.
Тепло передается только от горячего объекта к более холодному. Поэтому радиатор может работать только тогда, когда температура компонента выше, чем температура охлаждающей жидкости на выходе из радиатора. Например, если ядерный реактор работает при 2000 К, радиатор должен работать при 2000 К или меньше.
- Реактор от COADE. Реактор работает при температуре 2907К, а в радиатор поступает теплоноситель при 2400К.
Разница между температурами на входе и выходе из радиатора зависит от многих факторов, но обычно мы хотим максимально возможной разницы.Эта разница в температуре особенно важна для выработки электроэнергии. Большая разница означает, что от источника тепла можно извлечь больше энергии. Это также означает, что для охлаждения компонента требуется меньше охлаждающей жидкости.
Это создает проблемы с реалистичным дизайном.
Общее решение — использовать два комплекта радиаторов, работающих при разных температурах: один низкотемпературный контур и один высокотемпературный. Он отлично работает, когда ваше низкотемпературное отходящее тепло составляет несколько киловатт от систем жизнеобеспечения и авионики.Необходимо найти другие решения для компонентов, которые должны храниться при низких температурах, но при этом выделяют мегаватты отходящего тепла, например, лазеры.
- Эта конструкция имеет три комплекта радиаторов с уменьшающейся площадью для различных температурных составляющих. Фактически четыре комплекта, если считать радиаторы модуля обитания (Радиаторы полезной нагрузки / авионики)
Для низкотемпературных высокотемпературных компонентов необходимо использовать тепловые насосы. Они могут перемещать отходящее тепло против температурного градиента, позволяя, например, радиатору 1000K охладить компонент на 500K.Однако это требует затрат энергии. Перемещение тепла с 500 К до 1000 К обходится насосу в 1 ватт на каждый перемещенный ватт. Реалистичный насос не будет эффективен на 100% и потребует более 1 ватта, чтобы переместить ватт отработанного тепла.
Pump_power = (Waste_heat * Tc / (Th — Tc)) / Pump_Efficiency
Pump_power — сколько ватт потребляют тепловые насосы. Waste_heat — это количество ватт, которое необходимо удалить из компонента. Tc — температура компонента. Th — температура радиатора в градусах Кельвина. Pump_efficiency — коэффициент.
- Холодильный цикл — это пример теплового насоса.
Как правило, охлаждающая жидкость должна быть жидкой. Это накладывает нижний и верхний предел температуры охлаждающей жидкости; любой холоднее, и он замерзнет и заблокирует трубы, любой более горячий он закипит и перестанет течь. Например, водяную охлаждающую жидкость можно использовать только при температуре от 273 до 373 К. Что еще более важно, он ограничивает разницу температур, которую можно получить от радиатора.
Большие перепады температур требуют, чтобы охлаждающая жидкость долгое время находилась внутри радиатора. Для этого требуются радиаторы большего размера или длинные обходные пути для труб. По мере того, как охлаждающая жидкость становится холоднее, она излучает меньшую скорость, а это означает, что последнее понижение температуры на 10 кельвинов может занять экспоненциально больше времени, чем первое понижение на 10 кельвинов. Есть сильная убывающая доходность.
Есть также структурные проблемы. Большие перепады температур вызывают термические нагрузки. Они могут быть слишком большими, чтобы справиться с ними.Легкие, напряженные радиаторы склонны плохо реагировать на любые боевые повреждения, что делает радиаторы слабым местом для любого военного корабля.
- Лонжероны опор радиаторов МКС. Разгоняемый космический корабль будет нуждаться в гораздо большей поддержке.
В целом, мы должны иметь в виду, что существует ограниченный диапазон температур между горячим и холодным концом радиатора, и что его рабочие характеристики не могут быть просто получены с помощью уравнения Стефана Больцмана для максимальной температуры.2 панель радиатора:
Мы можем видеть, что натрию требуется 17 секунд, чтобы остыть от 1000 К до точки, близкой к его температуре плавления 370 К. Любой кулер — и застынет в трубках. Если мы усредним излучаемые ватты, мы получим значение, близкое к 11,46 кВт. Это соответствует средней температуре излучения 545 К.
Наконец, радиатор испытывает нагрузку при ускорении космического корабля. Некоторые типы радиаторов ломаются или разлетаются при сильном ускорении, поэтому перед выбором конструкции необходимо учитывать характеристики космического корабля.
Сплошные радиаторы
Простая конструкция, используемая сегодня.
Он состоит из металлической пластины, через которую проходит полая трубка для прохождения охлаждающей жидкости. Отработанное тепло выходит из хладагента в материал радиатора, который излучает его от его открытых поверхностей.
Эта конструкция имеет довольно высокую массу на единицу площади и низкие температурные ограничения, что делает ее одной из худших конструкций.Максимальная температура — это то, что делает материалы радиатора твердыми и прочными, что важно, поскольку многие металлы быстро теряют прочность по мере приближения к своей температуре плавления.
Охлаждающая жидкость должна оставаться жидкой на протяжении всего цикла охлаждения, поэтому это ограничивает возможную разницу температур. Использование металлов, таких как олово, или солей, таких как натрий, позволяет улучшить разницу температур, но для их перекачивания требуется специальное, иногда нереактивное, иногда энергопотребляющее оборудование.
- Несколько радиаторов будут излучать тепло друг в друга и терять эффективность.
Расположение радиаторов вокруг космического корабля должно учитывать взаимное отражение, когда тепло одного радиатора перехватывается и поглощается другим радиатором. Это снижает их эффективность. Все, что больше двух радиаторов на ось, поглощает часть тепла другого радиатора … при четырех радиаторах только 70% тепла уходит в космос, при восьми радиаторах эффективность падает до 38%.2, если рассматривать только открытые панели.
Пока только радиаторы из углеродного волокна без покрытия, работающие на 800-1000 К, достигли такой плотности.
Альтернативная конструкция обеспечивает лучшую плотность за счет удаления контуров охлаждающей жидкости и насосов. Тепловая трубка имеет горячий конец и холодный конец, разделенные вакуумом.
- Тепловая трубка, отводящая отработанное тепло в радиатор.
Твердый хладагент выкипает и затем конденсируется на холодном конце, а затем рециркулирует за счет капиллярного действия или центробежного ускорения.Этот метод допускает высокие рабочие температуры и не требует насосов движущихся частей, но высокая масса на единицу площади сводит на нет многие из его преимуществ.
На военном корабле радиаторы — слабое место. Яркие, открытые и трудно защищаемые, в них легко попасть, а после повреждения они могут вывести космический корабль из строя. Они могут убить военный корабль, даже не пробивая броню. Избыточные радиаторы налагают массовый штраф. Покрытие радиаторов пластинами из брони значительно снижает их теплопроводность между охлаждающей жидкостью и открытыми поверхностями, что, в свою очередь, снижает их эффективность.
Решения по снижению уязвимости радиаторов включают направление их ребром к противнику, перемещение их в хвостовую часть корабля или использование выдвижных конструкций.
- Справа радиаторы открыты вражескому огню. Слева выступ корпуса защищает радиаторы от повреждений.
Если все радиаторы убраны, космический корабль должен полагаться на радиаторы для охлаждения. Источник тепла мощностью в мегаватт может выпарить тонну воды менее чем за семь минут, так что это будет работать только в течение очень коротких периодов времени.
Высокотемпературные твердотельные радиаторы сталкиваются с проблемами, такими как необходимость иметь дело с закипанием охлаждающей жидкости или необходимость выдерживать огромное давление для поддержания жидкости в сверхкритическом состоянии. Решение — использовать твердые металлические блоки вместо охлаждающей жидкости. Запуск этих блоков, как поезд по рельсам, позволяет использовать надежные радиаторы, которые могут выдерживать сильные ускорения и температуры вплоть до точек кипения блоков охлаждающей жидкости (в некоторых случаях 4000K, если рельсы активно охлаждаются). Чем меньше блоки, вплоть до размера шариков, тем быстрее они остывают и тем короче должна быть дорожка, что приводит к экономии массы и площади.
Движущиеся радиаторы
Одна из главных причин, по которым твердые радиаторы настолько массивны, заключается в том, что им нужны трубы для охлаждающей жидкости, насосы и теплообменники для отвода отработанного тепла от оборудования на открытые поверхности.
Чтобы значительно уменьшить плотность помещения, мы можем разработать радиатор, не требующий громоздких контуров охлаждающей жидкости. Вместо этого перемещаем радиатор.
Движущиеся радиаторы полагаются на сам материал радиатора, который перемещается через теплообменник в космос, чтобы отвести тепло, а затем обратно внутрь.2 оценки. Однако движущихся частей гораздо больше, а излучающие поверхности составляют лишь небольшую часть объема, занимаемого радиаторами. Если не будут использованы очень легкие материалы, опорная конструкция сведет на нет массовое преимущество такого радиатора.
- От High Frontier
В диско-барабанной конструкции теплообменник имеет форму барабана, катящегося по излучающему диску. Радиатор hoola-hoop представляет собой большой диск, удерживаемый на конце барабанным теплообменником.
- Шлевки ремня держатся ребром к солнцу.Угловые петли будут меньше страдать от повторного поглощения излучаемого тепла на внутренних поверхностях, что более важно при более высоких рабочих температурах.
Если колесо или петля заменяется гибким ремнем или ремнем с гусеничной связкой, его можно заставить двигаться по различным путям. «Радиатор с поясной петлей» может приблизить радиатор к космическому кораблю и снизить прочность конструкции, необходимую для выдерживания ускорений или вибраций.
Конфигурация проволочной петли использует черные углеродные волокна в качестве излучающей поверхности.Они выбрасываются из теплообменника и удерживаются на месте центростремительной силой. Использование материалов с высокой прочностью на разрыв позволяет создавать чрезвычайно легкие петли.
- С высокой границы. Для изготовления проводов используются углеродные нанотрубки.
Ролики могут направлять провода вместо центростремительной силы, тем самым становясь еще более легкой версией ленточного радиатора. Потребуются материалы с высокой прочностью на разрыв, так как это позволяет роликам и двигателям удерживать провода под напряжением, чтобы предотвратить их скольжение или спутывание.
Радиатор с вращающимся диском — это движущийся радиатор, центральным элементом которого является вращающийся диск. На ступицу разбрызгивается охлаждающая жидкость. Поверхностное натяжение жидкости с низким давлением пара заставляет ее растекаться в тонкую, ровную пленку по диску. Когда диск вращается, центростремительная сила заставляет пленку течь, пока она охлаждается, к желобам коллектора на краях. В этой конфигурации не используются тяжелые тепловые трубы и радиаторные насосы, но требуется использование жидкостей с очень низким давлением пара.Диск можно наклонять внутрь, наружу или наклонять, чтобы справиться с ускорением космического корабля.
Радиаторы с пузырьковой мембраной представляют собой трехмерную версию радиатора с вращающимся диском. Горячая охлаждающая жидкость разбрызгивается на надутую мембрану, в результате чего она растекается в тонкую пленку, которая очень эффективно теряет тепло. Вращение мембраны заставляет жидкую пленку собираться на экваторе пузыря, где она собирается и повторно используется.
Преимущества включают возможность использования охлаждающих жидкостей с высоким давлением пара и очень легкую конструкцию.К недостаткам относится необходимость удерживать пары под высоким давлением в емкости, которая должна оставаться легкой и прозрачной.
Электрические радиаторы
В упомянутых до сих пор конструкциях используются физические конструкции, удерживающие радиаторы на месте. Это накладывает некоторые ограничения, такие как необходимость оставаться в пределах температурных пределов опорных конструкций, а для более крупных радиаторов требуется тяжелая опора, чтобы выдерживать даже легкие ускорения.
Решением будет использование магнитных сил для удержания радиаторов на месте.Сильный магнит может заменить физические опорные конструкции для значительной экономии массы.
Примеры таких радиаторов включают радиатор с флюсовыми выводами. Магнитные поля удерживают твердые компоненты радиатора на месте. Теплопроводящие ленты передают тепло к магнитным компонентам.
Однако есть сложности. Большинство металлов теряют свои магнитные свойства при нагревании, становясь совершенно нечувствительными к магнитным полям выше точки Кюри.Требуется тщательный выбор используемых материалов и контроль температуры.
Радиатор с точкой Кюри работает примерно при температуре, при которой частицы металлической пыли теряют свой магнетизм. Железо, например, теряет ферромагнетизм при 1043К.
В радиаторе с точкой Кюри используются металлические опилки или даже капли жидкости. Они нагреваются до температуры выше точки Кюри и выбрасываются в космос подальше от космического корабля. Магнитное поле есть, но оно не влияет на них.Железо может выделяться при температурах до 3134 К и собираться при 1043 К, но кобальт имеет температуру Кюри до 1388 К, он естественно черный и кипит при 3400 К, что делает его лучшим охлаждающим средством. Небольшой размер частиц или капель жидкости позволяет излучать несколько мегаватт отработанного тепла на квадратный метр.
Когда частицы охлаждаются ниже точки Кюри, они восстанавливают свой ферромагнетизм. На них начинает действовать магнитное поле, и они возвращаются к космическому кораблю для сбора.
Магнитные радиаторы — отличное решение для боевых повреждений — в худшем случае противник нарушит охлаждение на несколько секунд. Однако они потребляют много энергии и требуют тяжелого оборудования для создания сильных магнитных полей. Любое неожиданное ускорение или толчок космического корабля могут рассеять весь материал, удерживаемый на месте магнитными полями.
Альтернативный электрический радиатор использует электростатические силы для удержания заряженных частиц на месте. Одним из примеров является пылевой радиатор, заряженный ETHER.Заряженные частицы движутся по силовым линиям и совершают эллиптические орбиты между теплообменником и точкой сбора. Подобно радиатору с жидкими каплями, заряженные частицы могут механически диспергироваться и эффективно собираться на другом конце с помощью ложек с противоположным зарядом.
Преимущество электростатических излучателей заключается в том, что они потребляют меньше энергии, поскольку создать сильный дифференциал зарядов легче, чем расширить сильное магнитное поле. Оборудование легче и менее чувствительно к изменениям температуры, поскольку не используется сверхпроводящее или криогенное оборудование, а заряженные частицы могут удерживать заряд при большей разнице температур, чем они могут сохранять свои магнитные свойства.
Однако заряд, переносимый частицами, может быть нейтрализован естественным солнечным ветром или при контакте с проводником. Это означает, что им нужен чистый короткий путь между теплообменником и точкой сбора.
Жидкокапельные радиаторы
Жидкокапельные радиаторы не используют никаких излучающих поверхностей — они подвергают охлаждающую жидкость непосредственно воздействию вакуума. Полученные в результате капли имеют невероятную площадь поверхности для своей массы, что обеспечивает быстрое охлаждение и чрезвычайно низкую поверхностную плотность.
Поскольку охлаждающую жидкость не нужно физически удерживать, ее можно нагреть до очень высоких температур и при этом очень быстро остыть. Для жидкостей нет ограничений по термическому напряжению, поэтому изменение температуры может быть сколь угодно резким или быстрым. Они не обязаны сохранять магнитные свойства или держать заряд. Этот калькулятор может дать приблизительное представление о производительности LDR. При 1300K и использовании капель размером 50 микрометров (мелкий туман) поверхностная плотность может составлять всего 0.2. Не включает массу теплообменника, каплеуловителя и коллектора.
Уже разработаны решения для таких проблем, как капли, сдуваемые солнечным ветром, сталкиваясь и сливаясь в более крупные капли или перемещаясь с разными скоростями внутри слоя капель.
Давление пара по-прежнему вызывает беспокойство — горячие жидкости в вакууме имеют свойство быстро испаряться. Необходимо использовать специальные охлаждающие жидкости с низким давлением пара, такие как жидкий галлий, алюминий или олово до 1200K, литий до 1500K.Посолить эти жидкости таким материалом, как графитовая «крошка» или покрыть их черными чернилами, необходимо для достижения высокого коэффициента излучения. Наножидкости могут позволить использовать жидкости даже с более высокими температурами. Достижение более высоких температур означает принятие высоких скоростей потерь теплоносителя или заключение излучающего объема в мембрану, которая конденсирует и собирает пары. Мембрана должна быть прозрачной при температурах излучения.
Капли в радиаторе с жидкими каплями должны быть расположены равномерно и на расстояниях, намного превышающих диаметр капли — это необходимо для предотвращения значительных потерь между отражениями.
Варианты жидкокапельных радиаторов в основном связаны с ограничением и направлением потока охлаждающей жидкости между точками выброса и сбора.
Прямоугольный LDR имеет каплеуловитель и коллектор одинаковой длины. Коллекторный рычаг можно сделать шире эмиттера для улавливания капель, отклонившихся от их траектории из-за неожиданных движений или ошибок в формировании капель. Можно было бы перемещать коллектор выше и ниже плоскости капли, чтобы перехватывать капли, когда космический корабль ускоряется, поскольку это приведет к отклонению листа капли от плоскости.
- Дизайн ICAN-II с прямоугольными жидкокапельными радиаторами.
Треугольный LDR экономит массу за счет использования маленькой сборной тарелки вместо длинной руки. Однако он в меньшей степени способен улавливать отклоняющиеся капли или компенсировать ускорение космического корабля.
- Треугольные варианты LDR
В некоторых конструкциях LDR отсутствуют длинные ответвления и мембраны, а вместо этого капли просто распыляются в космос.Импульс капель заставляет их следовать по траекториям, по которым они попадают обратно к коллекторам. Фонтан LDR стреляет каплями перед разгонным космическим кораблем. Их собирают, когда они остынут. Этот метод диспергирования капель позволяет получить максимально легкие конструкции, но есть риск потери капель.
- Капли падают с «передней части» космического корабля и попадают в коллекторные рукава в средней части.
Он лучше всего работает с космическими кораблями, которые плавно ускоряются в течение длительных периодов времени, например с ядерно-электрическими кораблями на межпланетных траекториях.LDR с душем рассеивает капли перед космическим кораблем, а коллекторы просто собирают их, как черпак. У него меньший риск рассеивания капель, чем у фонтанного LDR, но для этого требуется длинная насадка для душа.
Мембраны под давлением могут быть дополнением к любому жидкокапельному радиатору. Они заключают в себе объем, через который проходят капли. Преимущества включают повторную конденсацию паров из слишком горячих капель, улавливание случайных капель, обеспечение более высокой скорости капель и большую устойчивость к нестабильности капельного слоя.Однако они должны оставаться прозрачными для всех длин волн, на которых излучают капли, и удерживать давление паров газа. Это конкурирующие требования: поглощение на малых длинах волн достигается с помощью очень тонких мембран, в то время как высокое давление требует толстых мембран.
Радиаторы Advanced
Сфокусированные LDR с магнитной накачкой:
- Магнитно фокусируется коллекторным соплом.
Феррожидкости при низких температурах и жидкий металл при высоких температурах могут использоваться в качестве хладагента в жидкокапельных радиаторах.Они реагируют на вихревые токи и магнитные поля, позволяя перекачивать хладагент без каких-либо движущихся частей посредством магнитогидродинамики.
Магнитные поля также можно использовать для восстановления капельного листа. Циклические поля могут толкать и тянуть группу капель на расстояния, пропорциональные напряженности поля. Поля высокой напряженности могут позволить каплям простираться на несколько десятков метров, прежде чем они будут восстановлены. Они также позволят LDR компенсировать свою уязвимость к рассеянию и потере капель при ускорении космического корабля, удерживая капли на месте.
Вместе LDR может стать чрезвычайно легким для занимаемой площади, так как никакая физическая опорная конструкция не должна перекрывать его длину.
Газовые хладагенты:
Мы рассмотрели твердые и жидкие хладагенты. Также можно использовать газы.
Газовые теплоносители уже используются в ядерных реакторах. Двуокись углерода и гелий были выбраны, поскольку они инертны и выдерживают более высокие температуры, чем вода или натриевые охлаждающие жидкости.
В космосе главное преимущество газового хладагента состоит в том, что он может работать при гораздо более высоких температурах, чем жидкий или твердый хладагент.Тот же газ можно было запустить из ядерного реактора в трубы радиатора и обратно. Это также позволяет создавать надувные конструкции для радиаторов, которые могут быть намного легче, чем их жесткие аналоги.
- Радиаторы с надувными ребрами.
- Радиаторы с несколькими выдвижными ребрами.
- Надувные мешки проще и прочнее раскатывающихся плавников, но имеют меньшую площадь поверхности.
Однако есть ограничения и сложности. Горячий газ под давлением может быть очень химически активным.Хотя вы можете нагреть газ до температуры 3000K +, стенки труб, содержащих газ, также должны выдерживать эти температуры. Многие из сбережений массы, которые достигаются при эксплуатации радиатора при высоких температурах, теряются, пытаясь удержать газовый хладагент и выжить. Например, перекачка газа требует гораздо большей мощности на 1 кг перемещенного газа, чем перекачка жидкости.
Другой проблемой является очень низкая скорость передачи тепла между теплообменником и газом. Горячий газ с низкой плотностью, такой как нагретый гелий, может иметь теплопроводность в сотни раз ниже, чем жидкость, такая как расплавленный натрий.Это приводит к трудностям как на границе теплообмена, так и на границе излучающей поверхности.
Многие из этих проблем могут быть решены с помощью двухфазного контура охлаждающей жидкости, то есть он проводит часть своего времени как жидкость, а часть — как газ. До теплообменника охлаждающая жидкость находится в жидком виде. Он течет по трубам с помощью простых насосов. Теплообменник разделен на множество труб меньшего размера, чтобы увеличить площадь контакта между теплообменником и хладагентом.
За теплообменником охлаждающая жидкость расширяется.Падение давления позволяет ему закипеть в газ. Этот газ проходит через объем, закрытый герметичной мембраной. Благодаря комбинации расширения и декомпрессии и закона Стефана-Больцмана газ быстро охлаждается и конденсируется на стенках мембраны. Это образует тонкую пленку в условиях микрогравитации, которая может быть направлена к точкам сбора, где жидкость перекачивается обратно в теплообменник.
Пылевой плазменный излучатель:
В этом излучателе используется проводящая плазма, управляемая магнитными полями, для перемещения и управления частицами пыли.
Частицы пыли, взвешенные в плазме, ведут себя удивительным образом, и их все еще обнаруживают в области исследований пылевой плазмы. Интересные варианты поведения включают самоорганизацию в квазикристаллическую структуру, построение мостов, похожих на нити ДНК, через плазму или сбор в диски с пустыми центрами. Все это происходит из-за самоотталкивающих зарядов, которые частицы пыли получают внутри плазмы.
Лучшее понимание этого поведения может позволить радиатору сочетать в себе все полезные характеристики: широкий диапазон рабочих температур, очень низкую массу на квадратный метр, легкость манипулирования электромагнитными и электростатическими силами, низкую уязвимость к повреждениям и способность выдерживать сильные ускорения.
Плазма может быть довольно холодной и по-прежнему служить для манипулирования частицами пыли. Низкотемпературная плазма безопасна для манипуляций и довольно прозрачна для длин волн, на которых будут излучать частицы пыли, что означает, что она не нагревается или не уносится тепловым расширением.
В простом пыльном плазменном излучателе плазма была бы захвачена магнитными петлями, такими как корональные петли. По этим плазменным трубкам двигалась пыль. Более совершенные пылевые плазменные излучатели распыляют частицы пыли в плазму и заставляют ее самоорганизовываться в тонкие плоскости для получения максимальной площади излучающей поверхности.Простое изменение состояния ионизации частиц путем пропускания электрического тока через плазму позволило бы пыли слипаться и следовать линиям магнитного поля прямо обратно к коллектору. ,
Вычислительное моделирование радиаторов транспортных средств с использованием подхода пористой среды
1. Введение
Одним из основных компонентов системы охлаждения двигателя является радиатор. Автомобильные радиаторы, как правило, представляют собой компактные теплообменники с ребристыми трубками (HX) и состоят из впускных коллекторов, выпускных коллекторов, трубок и ребер, как показано на Рисунке 1. Проще говоря, радиатор работает с двумя жидкостями: воздухом и незамерзанием. водная смесь. Горячая водно-охлаждающая смесь протекает через трубки, а охлаждающий воздух проходит через ребра, что приводит к теплообмену между обоими потоками.
Рисунок 1.
Типичный 4-рядный радиатор трактора.
Из-за сильной конкуренции в автомобильной промышленности желательны радиаторы с лучшими характеристиками (более высокая охлаждающая способность, меньшие гидродинамические потери, меньший вес и т. Д.). Обычным инструментом определения тепловых характеристик радиаторов автомобилей являются экспериментальные испытания. Однако экспериментальное тестирование может оказаться невозможным из-за стоимости и трудозатрат. Базовое понимание прошлых экспериментальных данных и аналитического / вычислительного моделирования может значительно повысить эффективность этапа проектирования и разработки.Существуют методы, доступные для анализа HX, такие как средняя логарифмическая разница температур (LMTD) и эффективность-NTU (ε-NTU). Однако для этих методов требуются некоторые параметры, известные априори , такие как общие коэффициенты теплопередачи и / или отношения NTU для заданного HX. Не существует общих выражений для общих коэффициентов теплопередачи и / или соотношений ε-NTU, применимых для любого HX. Следовательно, эти параметры необходимо прогнозировать либо на основе аналитических выражений [1], экспериментальных данных [2, 3] и / или расчетных моделей [3–6]. От дизайнера требуется априорное знание этих параметров. Следовательно, реализация LMTD и / или ε-NTU невозможна, особенно для радиаторов транспортных средств, которые могут включать в себя нестандартные конфигурации ребер. В качестве альтернативы, анализ вычислительной гидродинамики (CFD) может применяться для прогнозирования тепловых характеристик радиатора. Однако CFD-анализ полноразмерных HX невозможен из-за чрезвычайно большого количества ячеек, необходимых для определения сложной природы HX; особенно плавниковые конструкции.Этот момент становится более проблематичным, когда количество ребер велико в случае радиаторов для тяжелых транспортных средств. Хотя ребра создают значительную сложность для проблемы, повторяющаяся и / или регулярная структура ребер позволяет моделировать на основе пористой среды. С вычислительной точки зрения этот подход предлагает некоторые уникальные преимущества. Сложный поток жидкости, протекающий через ребра, можно ввести в модель через параметры пористости. Хотя определение этих пористых параметров требует строгой, подробной вычислительной модели с очень мелкой сеткой, особенно в областях, в основном ответственных за жидкостное трение и теплопередачу, это моделирование может быть выполнено на типичной элементарной ячейке из-за повторяющейся природы плавники.Как только эти эффекты включены через параметры пористости, структура сетки резко упрощается, и, учитывая всю геометрию, количество степеней свободы системы снижается до допустимого числа (порядка 10 миллионов). Кроме того, пористое моделирование не требует создания сетки пограничного слоя, поскольку параметры трения и теплопередачи уже включены через параметры пористости.
1.1. Пористое моделирование
Пористое моделирование регулируется тремя моделями.Простейшей моделью является модель Дарси, предложенная Генри Дарси (1856 г.) во время его исследований по гидрологии водоснабжения Дижона [7]. Уравнение Дарси выражается как:
, где Δ p — перепад давления, l — длина трубы, V — средняя скорость, μ — динамическая вязкость и α — проницаемость пористой домен. Проницаемость зависит от свойств жидкости и геометрических свойств среды.Зависимость падения давления от скорости в уравнении Дарси линейна; поэтому уравнение Дарси применимо, когда поток ламинарный. По мере увеличения скорости зависимость падения давления от скорости становится нелинейной из-за сопротивления, вызванного твердыми препятствиями. На данный момент в литературе предложены две расширенные модели, а именно модель Форхгеймера и модель Форхгеймера-Бринкмана. Для умеренных чисел Рейнольдса, включая нелинейные эффекты, перепад давления определяется как уравнение Форхгеймера [7]:
Δpl = — (μαV + CFα12ρV2) E2
, где C F — безразмерная константа сопротивления формы, а ρ — плотность жидкости.Первый член обозначает вязкие характеристики пористого потока, а второй член (также называемый термином Форхгеймера) обозначает инерционные характеристики. Наконец, модель Форхгеймера-Бринкмана включает дополнительный член Лапласа в дополнение к уравнению Форхгеймера. Модель Форххаймера-Бринкмана выражается как [7]:
Δpl = — (μαV + CFα12ρV2 − μ˜∇2V) E3
, где μ˜ — эффективная вязкость. В общем, добавленный термин Лапласа (также известный как термин Бринкмана) устраняет влияние характеристик потока в тонком пограничном слое в пристеночных областях.Строго говоря, последний член становится важным для значений большой пористости (отношение объема жидкости к объему твердого вещества в пористой среде), что означает, что эффект незначителен для многих практических приложений, где обычно значение пористости относительно невелико. Eq. (3) без квадратичного члена известна как расширенная модель Дарси (или Бринкмана). Таким образом, модель Форхгеймера-Бринкмана является наиболее общей моделью, но включение членов Бринкмана и Форхгеймера в левую часть может вызывать сомнения, поскольку член Бринкмана подходит для больших значений пористости, однако существует неопределенность в отношении применимости Член Форхгеймера при больших значениях пористости [7].
Определение скорости в пористом моделировании задается с использованием двух различных описаний: поверхностная формулировка и формулировка физической скорости. Формулировка поверхностной скорости не принимает во внимание пористость во время оценки уравнений неразрывности, импульса и энергии. С другой стороны, формулировка физической скорости учитывает пористость при расчете уравнений переноса [8]. Уравнение неразрывности и переноса импульса для пористой области с использованием модели Форчаймера можно записать как [2]:
∂∂t (γρ) + ∇.(ΓρV →) = 0E4∂∂t (γρV →) + ∇. (γρV → V →) = −γ∇p + ∇. (γτ →) + γBf → — (γ2μαV → + γ3C22ρ | V → | V →) E5
, где γ — пористость, C 2 — коэффициент инерции для пористой области, а Bf → — член объемной силы.
Помимо моделирования потока, моделирование теплопередачи для пористого потока описывается с помощью двух моделей: (i) равновесной модели и (ii) неравновесной модели. Модель равновесия (модель энергии с одним уравнением) используется, когда пористая среда и жидкая фаза находятся в тепловом равновесии.Однако в большинстве случаев жидкая фаза и пористая среда не находятся в тепловом равновесии. Для таких случаев более реалистичной является неравновесная тепловая модель. В случае радиатора этот вопрос важен, поскольку разница температур между твердым телом (ребра) и жидкостью (воздух, проходящий через ребра) является движущим механизмом для передачи тепла [4]. Следовательно, неравновесная модель включает два уравнения энергии (также известные как модель энергии с двумя уравнениями): одно для жидкой области, а другое для твердой области.Связь этих двух моделей осуществляется через термин, который представляет теплопередачу между жидкостью и твердыми областями. Уравнения сохранения для двухэнергетической модели можно записать как [2]:
∂∂t (γρfEf) + ∇. (V → (ρfEf + р)) = ∇. [Γkf∇Tf- (ΣihiJi) + (τ¯¯V →)] + SFH + hfsAfs (Ц-Т) E6∂∂t ((1-γ) ρsEs) = ∇. ((1 − γ) ks∇Ts) + Ssh + hfsAfs (Tf − Ts) E7
, где нижние индексы `s’ и `f’ обозначают твердое тело и жидкость, соответственно. E — полная энергия, T — температура, k — теплопроводность, S — член источника энергии и () означает эффект переноса энтальпии за счет диффузии компонентов. Последний член в обоих уравнениях — это член связи, который моделирует теплопередачу между жидкой и твердой областями. В этом термине связи hfs обозначает коэффициент теплопередачи для границы раздела жидкость / твердое тело, а Afs обозначает плотность поверхности раздела, которая представляет собой отношение площади поверхности раздела жидкость / твердое тело и объема пористой зоны.
Через уравнения. (3) — (7), существует множество параметров, которые являются свойствами материала и фиксируются после выбора материалов для жидкости и твердого тела. С другой стороны, есть некоторые параметры (т.е. параметры пористости), которые зависят от материала, геометрии и условий потока. Эти параметры: γ , α , C 2 , hfs и Afs. Среди них , γ, и Afs являются чисто геометрическими параметрами и могут быть определены после того, как станет известна геометрия пористой структуры.В случае моделирования радиатора, как только геометрия ребер задана, эти два параметра можно определить заранее. Другие параметры зависят от расхода, что означает, что их необходимо определять для конкретных условий расхода. На данный момент эти параметры могут быть определены с помощью некоторых аналитических выражений [9–11], экспериментальных результатов (например, испытания в аэродинамической трубе) [4, 12], эмпирических корреляций [13] и / или расчетных моделей [14–21], которые обычно являются допустимыми. для представительной элементарной ячейки. Все эти подходы были реализованы в литературе для различных исследований по анализу микро / макро теплоотводов и HX.
1.2. Вычислительное моделирование теплообменников
Пористое моделирование может быть реализовано для любой геометрии, которая напоминала бы пористую структуру. Более того, если пористая структура имеет повторяющуюся природу, коэффициенты пористости могут быть получены посредством детального моделирования типичной элементарной ячейки с помощью аналитических, экспериментальных или вычислительных средств. Радиаторы являются очень хорошими примерами в этом случае, и подход пористого моделирования был реализован для анализа микро / макро стоков [9–12].Модель энергии с двумя уравнениями была реализована для анализа радиатора с прямыми ребрами [9] вместе с моделью Дарси и реализована для выполнения оптимизации трубы с внутренними оребрениями [10] и обсуждения влияния аспектного отношения и эффективной теплопроводности. по тепловым характеристикам микроотвода радиатора [11] вместе с расширенной моделью Дарси. Радиаторы имеют регулярную конструкцию; поэтому есть возможность получить аналитические выражения для оценки параметров пористости [9–11].
Рассматривая HX со сложной структурой ребер, вычислительное моделирование становится еще более сложной задачей; поэтому вычислительные модели обычно сосредотачиваются на определенных подкомпонентах HX, таких как типичная элементарная ячейка для ребристой конструкции [14–21], вентилятор радиатора [22] и впускной коллектор [23, 24]. Тепловые характеристики HX могут быть достигнуты простым увеличением производительности одной лишь конструкции ребер. Ребристая конструкция с более высокой теплопередачей при меньшем падении давления может значительно улучшить производительность всей системы.Чтобы исследовать тепловые характеристики конструкции ребер, экспериментальные [14–18] и / или вычислительные модели [14, 17, 19–21] могут быть реализованы для различной геометрии ребер. Более того, улучшение неравномерного распределения потока во впускном коллекторе может также повысить тепловые характеристики. Вычислительное моделирование неравномерного распределения потока может привести к повышению производительности HX [23, 24].
Анализ подкомпонентов может привести к качественному заключению о тепловых характеристиках HX, однако для количественной оценки тепловых характеристик требуется строгое 3-D моделирование всего HX.Поскольку строгое моделирование невозможно с вычислительной точки зрения, для количественного прогнозирования тепловых характеристик в литературе были представлены двухмерная модель [4], модели на основе гидравлического и теплового сопротивления [12, 25] и трехмерные мезомасштабные модели (с учетом макро-контрольных объемов). [26-29]. 2D модель была разработана для сравнения модели равновесия (тепловая модель с одним уравнением) и неравновесной тепловой модели (модель энергии с двумя уравнениями) для матрицы относительно небольшого размера типа HX [4]. Модель, основанная на сопротивлении, была реализована для прогнозирования гидродинамических и тепловых характеристик HX с ребрами из пенопласта и углерода, которая объединила множество различных корреляций из литературы для прогнозирования гидродинамического и теплового сопротивления [25].Успех модели сильно зависит от точности параметров пор. Для этого конкретного примера было доказано, что модель предсказывает гидродинамические и тепловые характеристики в пределах ± 15% от экспериментальных данных. Программное обеспечение для моделирования компактных теплообменников (CHESS) было разработано [26–28] как инструмент оценки и проектирования для промышленного использования, основанный на эмпирической корреляции пористых параметров для анализа ребристой части радиаторов автомобиля (за исключением впускной и выпускной коллекторы).Было продемонстрировано, что при использовании CHESS тепловые характеристики радиаторов различных транспортных средств были предсказаны в пределах ± 15% от экспериментальных значений. В качестве альтернативы, CFD-модель на основе пористого моделирования для потока жидкости и мезомасштабное моделирование тепловых характеристик на основе ε-NTU использовалось для поперечного потока HX воздух-воздух [29], чтобы исследовать влияние неравномерности распределения на тепловые характеристики. 3D модель CFD в сочетании с подходом пористой среды была разработана для исследования гидродинамических характеристик пластинчатого ребра HX, в котором параметры пористости также были определены с использованием подробной модели CFD на элементарной ячейке [30].
Полноразмерное трехмерное тепловое моделирование относительно небольшого компактного HX было проведено с различными конфигурациями ребер и параметрами теплопередачи и коэффициента трения, которые можно использовать в сочетании с методом LMTD или ε-NTU [5]. Поскольку размер HX был небольшим, создание сетки не представляло проблемы, и вычислительная модель была использована для проектирования впускного коллектора для повышения производительности. Учитывая размер радиатора автомобиля, такой подход не подходит. Температурный и структурный анализ радиатора для тяжелых грузовиков, который имел ребристую структуру как со стороны жидкости, так и со стороны воздуха, был выполнен с использованием коммерческого программного обеспечения CFD FLUENT ® [31].Соотношение Форхгеймера использовалось для пористого моделирования вместе с экспериментальными данными. Модель энергии с одним уравнением использовалась вместе с усредненной эквивалентной теплопроводностью. Локальные коэффициенты теплопередачи и распределение давления, полученные из термического анализа, использовались в качестве граничного условия для структурного анализа методом конечных элементов, посредством которого были получены термические напряжения и деформации.
Одной альтернативой всем этим подходам может быть подход к моделированию радиатора транспортного средства с использованием пористой среды, где параметры пористой среды также выводятся на основе строгого моделирования CFD на элементарной ячейке.Более того, эту процедуру можно выполнить с помощью коммерческого программного обеспечения CFD, которое будет иметь очень сильные возможности построения сеток, решения и постобработки. Однако реализация двухтемпературного уравнения энергии имеет решающее значение для точного прогнозирования, особенно для радиаторов транспортных средств. Это может быть непросто с коммерческим программным обеспечением. На этом этапе FLUENT ® может быть жизнеспособным решением, поскольку возможность двухтемпературной модели была включена в версию 14.5. Совсем недавно на основе двухтемпературной модели было проведено вычислительное моделирование автомобильного радиатора с трубчатым оребрением, и охлаждающая способность радиатора для тяжелого транспортного средства была оценена без каких-либо эмпирических и / или экспериментальных данных. [32].В следующем разделе описывается вычислительная методология такой вычислительной модели. Такой подход может позволить моделирование CFD стать эффективным инструментом оценки и проектирования радиаторов автомобилей. Хотя предложенная методика расчета обсуждается для радиатора транспортного средства, она также может быть реализована для любого компактного HX с повторяющейся структурой ребер, что является важной проблемой для многих промышленных приложений.
2. Вычислительное моделирование
Предлагаемая вычислительная методология реализована для радиатора коммерчески доступного грузового автомобиля большой грузоподъемности (а именно трактора) с 4 рядами и 39 столбцами, как показано на рисунке 1.Трактор, на котором используется изготовленный радиатор, оснащен двигателем Perkins мощностью 64 л.с., для которого, согласно данным каталога, требуется минимальная мощность охлаждения 55 кВт. По данным тракторной компании, охлаждающая способность этого радиатора составила 55,8 кВт в результате собственных экспериментов по протоколу SAE-J1393 [33]. Данные каталога приведены в таблице 1. Конструкция ребер, используемая в этом радиаторе, представляет собой структуру с волнистыми ребрами (WF), которая является типичной конструкцией, используемой в радиаторах транспортных средств из-за ее превосходных тепловых характеристик.Выбранная конфигурация волнистых ребер составляет 84 мм в длину.
Вычислительная процедура начинается с определения параметров пор для данной конфигурации сетки. Геометрические параметры определены с помощью CAD-модели. С другой стороны, для определения параметров потока необходимо провести параметрическое исследование элементарной ячейки с высоким разрешением, которая состоит из одного повторяющегося участка ребристой структуры. Для определения коэффициентов пористой среды необходимо анализировать поле течения только для участка с ребристой структурой (моделирование физических ребер).Чтобы проверить извлеченные коэффициенты пористой среды, поле потока в элементарной ячейке вместе с включенной областью жидкости выше и ниже по потоку необходимо смоделировать как с использованием фактической геометрии ребер, так и пористого моделирования. Этот анализ необходимо выполнить только один раз для каждой интересующей конфигурации сетки.
2.1. Определение пористых параметров
Анализ ребра осуществляется в три основных этапа:
Моделирование модели с прямым ребром элементарной ячейки с использованием различных скоростей впуска воздуха и получения результирующего падения давления на ребре.
Подгонка кривой второго порядка к собранным данным зависимости давления от скорости дает соотношение Дарси-Форххаймера как:
Δpl = a V + b V2 = — (μαV + C212ρV2) E8
, где a и b — коэффициенты, характеризующие течение.
Получение коэффициента инерции и коэффициента вязкости с использованием извлеченных коэффициентов на этапе (b) как:
Получение коэффициентов пористой среды на основе потока сопровождается определением входных параметров для моделирования теплопередачи.Необходимыми входными параметрами являются средний коэффициент теплопередачи (HTC) и плотность межфазной поверхности (IAD) для модели энергии с двумя уравнениями. Средний коэффициент теплопередачи получается в результате постобработки FLUENT ® , который можно рассчитать, используя следующее соотношение:
Эталонная температура в приведенном выше уравнении — это средняя температура воздуха между входом и выходом оребренного канала.
2.2. Моделирование физических плавников
Элементарная ячейка модели с волнистыми плавниками, Модель-A, показанная на рисунке 2 (а), анализируется для получения параметров пористой среды.Параметры потока получаются с использованием соотношения Форхгеймера. Модель-A моделируется с использованием различных чисел Рейнольдса для получения кривой Форхгеймера. После получения параметров анализируется Модель-B, которая представляет собой элементарную ячейку волнистого ребра с дополнительными областями вверх и вниз по потоку, как показано на Рисунке 2 (b). Поскольку воздушные домены (без ребер) прикреплены на входе и выходе из пористой области, площадь потока сужается (на входе в пористую область) и расширяется (на выходе из пористой области) на границах раздела этих областей. домены.Чтобы уловить физику, вводятся граничные условия пористого скачка, чтобы соответствовать результатам двух моделей [8]. Граничные условия для Модели-A устанавливаются следующим образом: граничные условия скорости на входе и выходе давления задаются для входа и выхода ребра соответственно. Граничное условие стены применяется для верхней и нижней стен. Граничное условие постоянной температуры стенки назначается стенкам как тепловое граничное условие (которое близко к реальной ситуации, поскольку изменение температуры в направлении z мало).Периодическое граничное условие используется для правой и левой сторон. Для модели B дополнительная симметрия восходящего потока и нисходящая симметрия назначаются для восходящих и нисходящих доменов. Для обеих моделей используется метод SIMPLE с подходом на основе наименьших квадратов для восстановления градиента. Кроме того, используются стандартная схема для давления и схемы второго порядка для импульса, турбулентной кинетической энергии и скорости турбулентной диссипации. Коэффициенты релаксации установлены на значения по умолчанию.Для обоих моделей минимальная сходимость 1 × 10 −5 получается для всех остатков. Одним из важных шагов является определение подходящей модели турбулентности. На этом этапе можно использовать некоторые эталонные решения, эмпирические / экспериментальные результаты для определения соответствующей модели турбулентности. Для рассматриваемой конструкции ребра используется реализуемая модель турбулентности k-ε со стандартной функцией стенки (подробное обсуждение обоснования использования этой модели турбулентности можно найти в другом месте [32]).
Рисунок 2.
(a) Модель-A: домен элементарной ячейки WF и (b) Модель-B: элементарная ячейка WF с доменами входа и выхода.
| Определение | Значение |
|---|---|
| Скорость вращения двигателя [об / мин] | 2200 |
| Температура на входе [° C] | 86,5 |
| 81 | |
| Температура окружающей среды [° C] | 31 |
| Массовый расход на входе [кг / с] | 2.41 |
| Скорость воздуха [м / с] | 7 |
| Отвод тепла [кВт] | 55,8 |
Таблица 1.
Данные каталога для четырехрядного радиатора.
| Описание | Единица | ||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Длина домена | 84 | мм | |||||||||||||||||||||||
| Количество ячеек | |||||||||||||||||||||||||
| Моделирование турбулентности | k-ε-реализуемое | ||||||||||||||||||||||||
| Объем ребра | 2,2567 × 10 -7 | м 3 | |||||||||||||||||||||||
| 10 Общий объем 91 6 | м 3 | ||||||||||||||||||||||||
| Пористость | 0,9473 | ||||||||||||||||||||||||
| Гидравлический диаметр | 0,00241 | м | |||||||||||||||||||||||
| Интенсивность турбулентности | 0.058 | ||||||||||||||||||||||||
| Длина турбулентности | 0,000169 | м | |||||||||||||||||||||||
| Метод решения | SIMPLE | ||||||||||||||||||||||||
| Время расчета / на моделирование | 30 | мин. параметры для моделирования ВФ элементарной ячейки. После этого необходимо выполнить анализ независимости сетки, чтобы гарантировать независимость от сетки решений. Было замечено, что приблизительно 4 900 000 ячеек с 30 слоями граничной сетки для ребер дает независимый от сетки результат для этой конкретной конфигурации ребер.Таблица 2 содержит входные параметры для Model-A. На рис. 3 падение давления в конструкции оребрения нанесено в зависимости от скорости, а кривая второго порядка аппроксимируется данными моделирования. Соответствующие коэффициенты инерции и вязкости определены как 17,3 и 4,01 × 10 6 соответственно. Параметры теплопередачи получены из моделирования модели-B. Для моделирования Модели-B входные параметры определены как 7,0 м / с для скорости на входе, 304,2 K для температуры на входе и 359 ° C.7 К для температуры стенок оребрения в соответствии с табличными данными каталога. Средний коэффициент поверхностной теплоотдачи и настроенные коэффициенты скачка пористости для элементарной ячейки волнистого ребра представлены в таблицах 3 и 4 соответственно. Рис. 3.Физическое моделирование давления ВФ в элементарной ячейке в зависимости от скорости.
Таблица 3.Параметры пористости WF.
Таблица 4.Коэффициенты скачка пор для элементарной ячейки ВФ. 2.3. Моделирование плавников с помощью моделирования пористостиПосле получения коэффициентов пористости поле потока воздуха можно смоделировать с использованием моделирования пористости. Для этого анализа присоединяются восходящие и нисходящие домены, как показано на рисунке 4 (а). Для проверки пористого моделирования результаты сравниваются с физическим моделированием плавников.Для модели пористого ребра используется сетка с шестигранной разверткой. Сетка пористой модели (рис. 4 (б)) состоит из 5320 ячеек. После завершения процесса построения сетки назначаются граничные условия. Помимо конфигураций граничных условий физического ребра, вводятся дополнительные граничные условия с пористым скачком, чтобы соответствовать моделированию физического ребра. Все настройки решателя принимаются такими же, как и при моделировании физических плавников. После получения коэффициентов потока пористой среды, коэффициентов скачка пористой среды и параметров теплопередачи на основе моделирования элементарной ячейки волнистого физического ребра и моделирования пористой среды выполняются с одинаковыми входными параметрами для проверки моделирования пористой среды.На рисунке 5 (а) сравнивается усредненное по сечению падение давления для моделирования физического ребра и пористой среды. На рисунке 5 (b) показано такое же сравнение для падения температуры, усредненного по массовому расходу. Как видно из рисунка 5, приемлемая последовательность достигается с помощью пористого моделирования. Следует отметить, что для пористой среды требуется всего 5320 ячеек на ячейку ячейки; с другой стороны, для физического плавника требуется 4 900 713 клеток. Если смоделировать полноразмерный радиатор с физическими ребрами, необходимое количество ячеек составит примерно 20 миллиардов, что невозможно проанализировать даже с помощью современных вычислительных технологий; поэтому, используя подход пористого моделирования, полноразмерная модель может быть проанализирована за разумное время вычислений вместе с разумной точностью.Согласно представленным результатам, характеристики перепада давления и температуры согласованы между физическим ребром и пористой средой. Контурные изображения для y + , распределение скорости и температуры по ребру представлены на рисунке 6. Из результатов модели B видно, что значения y + приемлемы по сравнению с результатами анализа (для модели турбулентности SST максимум y + значение должно быть меньше 1.0) [8], а распределения скорости и температуры имеют удобные характеристики. Рис. 4.(a) пористая модель элементарной ячейки с входными и выходными областями и (б) конфигурацией сетки. Рис. 5.Сравнение физической WF и пористой модели: (a) среднее падение давления в разрезе и (b) среднее падение температуры в разрезе по массе-расходу. Рис. 6.(a) y + контур, (b) распределение скорости и (c) распределение температуры по WF. Рис. 7.Распределение скорости воздуха (а) и температуры (б). 2.4. Моделирование радиатораТрехмерная CAD-модель 4-рядного 39-колонного радиатора подготовлена с использованием программного обеспечения CAD. После формирования 3-D модели процесс построения сетки продолжается. Ребра, верхний и нижний по потоку и трубные области зацеплены с элементами шестигранного типа, а верхний и нижний резервуары зацеплены с четырехэлементами. Трубки соединены сеткой пограничного слоя, имеющей два слоя с высотой первого слоя 0,1 мм. Сгенерированная сетка состоит из 53 355 356 ячеек со средним значением асимметрии 0.178. Граничные условия на входе массового расхода, выходе давления, скорости на входе, выходе давления, стенке перед потоком и стенке ниже по потоку задаются для входа воды, выхода воды, входа воздуха, выхода воздуха и границы внешней поверхности областей входа и выхода, соответственно. , Скорость воздуха на входе принята равной 7,0 м / с при температуре на входе 304,2 К, а массовый расход воды — 2,41 кг / с при температуре на входе 359,7 К в соответствии с данными каталога. Схема второго порядка против ветра используется для импульса, турбулентной кинетической энергии (TKE) и скорости турбулентной диссипации (TDR).Коэффициенты релаксации выбираются равными 0,05 для импульса, 0,3 для TKE и TDR и 0,4 для турбулентной вязкости, чтобы получить оптимальную скорость сходимости и время решения. Коэффициент теплопередачи между ребрами и воздухом принят равным 170 Вт / м 2 K со ссылкой на предыдущее моделирование элементарной ячейки. Сходящееся решение получается после 472 итераций, когда минимальная невязка меньше 1 × 10 -4 . Моделирование выполняется на рабочей станции DELL T5600 (Intel ® Xeon ® , 3.30 ГГц, 2 процессора, 16 ядер, 128 ГБ ОЗУ). Общее время растворения составляет примерно 12 часов 40 минут. Рис. 8.Линии тока со стороны воды (а) окрашены в соответствии со скоростью и (б) окрашены в соответствии с температурой. Распределения скорости и температуры в поперечном сечении для линий тока со стороны воздуха и со стороны воды представлены на рисунках 7 и 8 соответственно. Градиенты температуры успешно достигаются в направлениях z- и y-, как и ожидалось.Температура на стороне воздуха увеличивается в направлении потока в результате передачи тепла со стороны воды, в то время как температура со стороны воды снижается в направлении потока. Поток не распределяется между трубками равномерно, как показано на рисунке 8 (а). Однако для улучшения характеристик радиатора необходимо уменьшить неравномерное распределение потока в коллекторе [22–24]. Таким образом, можно четко сказать, что существующий дизайн нуждается в улучшении. Это неравномерное распределение потока по трубкам также способствует повышению температуры в направлении x —.Согласно моделированию, средняя температура воды на выходе составляет 354,3 K, а общее падение температуры воды через радиатор рассчитывается как 5,4 K, что дает общую теплоемкость: Q = m =Cp ΔT = 2,41 x 4208 x 5,36 = 54,4 кВт E12 Перепад давления воды, который также является важным параметром производительности радиаторов, составляет 6,5 кПа. По данным каталога, температура воды на выходе, перепад температуры на радиаторе и холодопроизводительность 354.2 К, 5,5 К и 55,8 кВт. Те же параметры оказались равными 354,3 К, 5,4 К и 54,4 кВт с предложенным анализом CFD. Отклонение результатов CFD от каталога составляет 2,5%, что вполне приемлемо для термического анализа. Более того, предлагаемая модель решает проблему за разумное время вычислений. Учитывая точность результата и вычислительную стоимость, предложенная методика может быть использована в качестве инструмента оценки и проектирования автомобильных радиаторов. 3. Заключительные замечанияХотя повторяющиеся структуры ребер создают проблему для компьютерного моделирования радиатора, повторяющийся характер также позволяет эффективно моделировать пористую среду.Более того, опять же из-за повторяющегося характера, параметры пористости могут быть получены с помощью CFD-моделирования типичной элементарной ячейки с высоким разрешением. Успешная реализация пористого моделирования может привести к резкому сокращению вычислительных затрат и времени. Реализация вычислительной методологии с помощью коммерческого программного обеспечения также выигрывает от мощных возможностей построения сеток, решения и постобработки. Как показано, CFD-анализ радиатора с использованием подхода пористой среды дает разумные и надежные результаты.При использовании анализа CFD стоимость проектирования может быть значительно снижена за счет упрощения процесса экспериментальных испытаний. Параметры пористости с заданной геометрией ребер могут быть получены в течение нескольких часов, что может обеспечить гидродинамическую и термическую оптимизацию радиатора. Оптимизация радиаторов с точки зрения размера и веса желательна, чтобы соответствовать ограничениям в конкурентной автомобильной промышленности. Эффективная вычислительная модель позволяет выполнять процесс оптимизации с помощью вычислений для ряда различных проектных параметров.Кроме того, могут быть разработаны более реалистичные вычислительные модели, такие как включение вентилятора радиатора в модель или включение оборудования под капотом вместе с увеличением вычислительной мощности компьютеров. Вдобавок ко всему, объединение поля потока и температуры со структурным анализом может привести к гораздо более эффективным и надежным конструкциям радиаторов. . Калькулятор ромбовРомб в форме a = длина сторон Использование калькулятораВычислить некоторые переменные ромба в зависимости от предоставленных входных данных. Вычисления включают длину сторон, углы, диагонали, высоту, периметр и площадь ромба. Ромб — это четырехугольник, противоположные стороны которого параллельны, а все стороны равны по длине. Ромб, у которого все углы прямые, называется Единицы: Обратите внимание, что единицы длины показаны для удобства. На расчеты они не влияют. Единицы измерения указывают порядок вычисленных результатов, например футы, футы 2 или футы 3 . Можно заменить любой другой базовый блок. Формулы и ограничения ромбаУглы наклона: A, B, C, D
Площадь: Кс A и B в радианах, K = ah = a 2 sin (A) = a 2 sin (B) = pq / 2 Высота: h
Диагонали: p, q
Периметр: PP = 4a Rhombus Вычислений:Следующие формулы, основанные на приведенных выше, используются в этом калькуляторе для выбранных вариантов расчета.
СсылкиЦвиллинджер, Даниэль (главный редактор). Стандартные математические таблицы и формулы CRC, 31-е издание New York, NY: CRC Press, p. 323, 2003. Математический форум: Спросите доктора математики FAQ: Вайсштейн, Эрик У. «Ромб». Из , Калькулятор сферФорма сферы r = радиус Использование калькулятораЭтот онлайн-калькулятор рассчитает 3 неизвестных значения сферы с учетом любой 1 известной переменной, включая радиус r, площадь поверхности A, объем V и длину окружности C.Он также даст ответы для объема, площади поверхности и окружности с точки зрения PI π. Сфера — это набор точек в трехмерном пространстве, которые расположены на равном расстоянии r (радиус) от данной точки (центральной точки). Единицы: Обратите внимание, что единицы показаны для удобства, но не влияют на вычисления. Единицы измерения указывают порядок результатов, например футы, футы 2 или футы 3 .Например, если вы начинаете с мм и знаете r в мм, ваши вычисления приведут к A в мм 2 , V в мм 3 и C в мм. Формулы сферы для радиуса r:
Объем сферы \ [V = \ frac {4} {3} \ pi r ^ 3 \] \ [V \ около 4.{1/3} \] \ [r = \ sqrt {\ frac {A} {4 \ pi}} \] \ [r \ приблизительно 0,2821 \ sqrt {A} \] \ [r = \ frac {C} {2 \ pi} \] \ [r \ приблизительно 0,1592C \] Окружность сферы \ [C = 2 \ pi r \] \ [C \ около 6.{1/3} \] \ [C = \ sqrt {\ pi A} \] \ [C \ приблизительно 1.77245 \ sqrt {A} \] Расчет сфер:Используйте следующие дополнительные формулы наряду с формулами выше.
, |